11.2: Ion-Dipole Forces
- Page ID
- 42002
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ion-Dipole Interactions
Ion-Dipole Forces are involved in solutions where an ionic compound is dissolved into a polar solvent, like that of a solution of table salt (NaCl) in water. Note, these must be for solutions (and not pure substances) as they involve two different species (an ion and a polar molecule).
\[ Na^+ ↔ (H_2O)_n \nonumber \]

Figure \(\PageIndex{1}\): Ion-Dipole interaction. Note the oxygen end of the dipole is closer to the sodium than the hydrogen end, and so the net interaction is attractive (see figure \(\PageIndex{2}\)).
The name "Ion dipole forces" describes what they are, which simply speaking, are the result of the Coulombic electrostatic interactions between an ion and the charged ends of a dipole. Note that here, the term "Intermolecular Force" is a misnomer, even though it is commonly used, as these are the forces between ions with molecules possessing a dipole moment, and ions do not have to be molecular. To gain an understanding of the nature of these forces we can start by looking at the Coulombic potential between two ions (Equation 11.2.1) and ask the following question.
Exercise \(\PageIndex{1}\)
What is the difference between Coulombic Ion-Ion and Ion-Dipole interactions in terms of the distance between the particles?
- Answer
-
One is an inverse distance relationship, the other is an inverse distance square relationship. The following material explains this.
In the introduction to this chapter we saw that two charged particles q1 and q2 had a potential energy related to Equation 11.2.1, and this describes the potential energy interaction between two ions.
\[\underbrace{E= k\dfrac{q_1q_2}{r}}_{\text{ ion-ion potential }}\label{11.2.1}\]
For ion-dipole interactions the interaction is between a dipole moment (\(\mu\)), which is really a vector with a magnitude of \(\delta \cdot r\), where \(\delta\) is the value of the partial charge in the dipole moment (\(\delta ^+\) or \(\delta ^-\), noting they are of the same magnitude, just opposite in sign), with an ion of charge q. (We are using \(\delta\) to indicate the partial charge in the dipole just to prevent it from being confused with q, the charge of the ion).
So there are two ion-dipole interactions, with one being attractive and the other repulsive, as shown in figure \(\PageIndex{2}\).
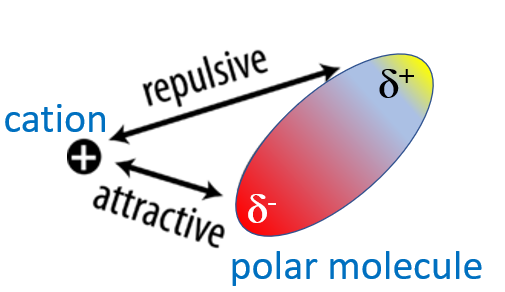
Figure \(\PageIndex{2}\): Interactions between a positive cation and a polar molecule.
Now if you think about it, the cation repels the positive end of the dipole and attracts the negative end, so the negative end is closer to the cation than the positive end. This means the attractive energies are greater than the repulsive (as they are closer together, the r of coulombs law is in the denominator of eq. So the net force is attractive since the radius (in the denominator of Coulombs Law, Equation \(\ref{11.2.1}\)) for the +/- attraction is smaller than the radius for the +/+ repulsion. This difference is greatest when the polar molecule is "touching" the cation, and as they become further separated the relative differences in the radii between the two interactions become less, and at great distances they become equal, making these short range forces. This can be understood by looking at Figure \(\PageIndex{3}\).
Figure \(\PageIndex{3}\): Showing how the relative distance between the ion-dipole interaction falls off as they become separated. In the top interaction the +/+ radius is 3 times as far as the +/- (300 pm to 100 pm), but in the bottom it is 5/3rds as far (500 pm to 300 pm) and so the difference between the repulsive and attractive forces is less. That is, at large distances the distances between the ion and the two partial charges narrow with a consequent cancelation of the effect.
The result in an inverse square of the distance function (1/r2) for the decrease for ion-dipole interactions as compared to a 1/r effect for ion-ion interactions, as shown in Equation \ref{11.2.2}.
\[\underbrace{E\: \propto \: \dfrac{-|q_1|\mu_2}{r^2}}_{\text{ ion-dipole potential }} \label{11.2.2} \]
or
\[\underbrace{E=-k\dfrac{|q_1|\mu_2}{r^2}}_{\text{ ion-dipole potential }} \label{11.2.3}\]
(ion-dipole potential)
- \(\alpha\) means "proportional to" (the proportionality constant depends on the medium)
- \(r\) is the distance of separation.
- \(q\) is the charge of the ion ( only the magnitude of the charge is shown here.)
- \(k\) is the proportionality constant (Coulomb's constant).
- \(\mu\) is the permanent dipole moment of the polar molecule (sections 8.7.4.2 and 8.8).
From section 8.7 and 8.8 we treat define the dipole moment by the following equation
\[ \vec{\mu} = q \; \vec{r} \label{11.2.4} \]
where q is the partial charge of each end of the dipole (\(\delta^+ \;or \; \delta^-\)) and r is the separation between the charges within the dipole, but these symbols are being used to describe the ion interactions in equations 11.2.1-11.2.3, and so we will rewrite eq. \(\ref{11.2.4}\) with \(\delta\) instead of q representing the magnitude of the partial charge of the dipole (\(\delta^+ \; or \; \delta^-\)) and \(\vec{d}\) representing the distance between the center of positive and negative charge in the polar molecule \(\vec{r}\).
\[ \vec{\mu} = \delta \; \vec{d} \label{11.2.5} \]
Realize eq. 11.2.4 is the most common way to describe the dipole moment, but when looking at ion-dipole interactions there are two types of charges (those of the ion, and the partial charge separations of the dipoles), and two types of distance, the distance between the ion and dipole, and the distances between the dipoles. So for this section we will rewrite eq. 11.2.4 in terms of 11.2.5.
Note
Equations \ref{11.2.1} and \ref{11.2.3} are dimensionally equivalent. This is because \(\mu\) has the units charge times distance (Equation \ref{11.2.4}), and if you substitute eq. 11.2.5 into eq. 11.2.3, you will see it is dimensionally equivalent to 11.2.1
Key differences between ion/ion and ion/dipole interactions
- Ions have integer charges (1,2,3.. for cations and -1,-2,-3... for anions), while dipole's have partial charges (\(\delta^{+\:or\:-}\)) and the partial charges can be very small fractions.
- Ion-ion interactions fall off slower than ion-dipole. Tripling the distance between two ions reduces the energy by 1/3, while tripling the distance between the ion and a dipole reduces it by 1/9. That is, one is inversly proportional to the distance between them (1/r) and one is proportional to the inverse square of the distance (1/r2).
Exercise \(\PageIndex{2}\)
Why does the Coulombic ion-dipole equation (\ref{11.2.2}) have a negative sign and the absolute value on the charge, while the ion-ion equation (\ref{11.2.1}) does not?
- Answer
-
- The ion dipole interactions are always attractive resulting in a lowering of the potential energy. Since \(\mu\) is always positive, but q can be positive (cation) or negative (anion), so we use it's absolute value and add the negative sign to ensure there is a lowering of energy. For ion-ion, they can be attractive (+/-) which results in a negative E, or repulsive (+/+ or -/-), both of which result in a positive E.
Exercise \(\PageIndex{3}\)
How does the ion-dipole equation show that ion dipole interactions are shorter range than ion-ion interactions?
- Answer
-
- The ion-ion interaction energy is inversely proportional to the distance between the ions (1/r), while the ion-dipole energy is inversely proportional to the square (1/r2). So doubling the distance decreases the first by a factor of 2, and the later by a factor of 4 (and tripling the distance decreases the first by a factor of 3, and the later by a factor of 9). So ion dipole interactions are much shorter ranged.
It also needs to be understood that these equations are based on electrostatic interactions and molecules in a solution are rotating and vibrating and actual systems are quite complicated, with the medium (molecular environment) influencing the actual behavior. Coulombs constant is based on the permittivity of an electric field in a vacuum, and actual chemical systems are not in a vacuum, and so the permittivity will be different. The important thing to realize is that these interactions are Coulombic in nature, and these equations show this in terms of the magnitude of the charges and their distances from each other, which are the two major factors influencing the strength of intermolecular forces. In this class we will not be calculating dipole moments or the magnitudes of them, but understanding how to read the equations, and developing qualitative understandings that allow us to predict trends.
It should also be understood that not all ion-dipole interactions are in solutions. For example, hydrated salts where the water is "captured" in a crystal's interstitial regions (holes in the lattice) are ion-dipole in nature. In fact these can be necessary to form certain crystalline geometries as the polar water molecule can reduce the repulsion of like charges within a lattice. We will look at crystals in the next chapter.
Periodic Trends and Hydration Energy
The enthalpy of hydration is often defined as the energy released when a mole of a gaseous cation is dissolved in water, and is related to ion-dipole forces.
\[M^+_{(g)} + water \rightarrow M^+_{(aq)}\]
The smaller the cation, the closer the particles, and for a given charge the stronger the ion-dipole forces and the greater the enthalpy of hydration (more exothermic). This is exemplified by the enthalpies of hydration in Table \(\PageIndex{1}\). It needs to be noted that the above definition aligns with thermodynamic principles, where greater means more exothermic (negative). That is, from the first law of thermodynamics a positive energy change occurs when is energy added to the system (endothermic) and a negative energy change occurs when is is released (exothermic). The small Lithium ion has a lower value (-515 kJ/mol) than the larger Cesium (-263 kJ/mol), meaning it is more exothermic, and more energy is released. This may be easier to see by looking at the back reaction, where you need to add energy to remove the hydrated ion and place it in the gas phase, since adding energy is endothermic, the reaction as drawn must be exothermic.
| Cation | Ionic Radius (pm) | Enthalpy of Hydration (kJ) |
|---|---|---|
| \(Li^+\) | 90 | -515 |
| \(Na^+\) | 116 | -405 |
| \(K^+\) | 152 | -312 |
| \(Rb^+\) | 166 | -296 |
| \(Cs^+\) | 181 | -263 |
From general chemistry 1 students should know the trends in the sizes of ions, and based on these, they should be able to predict the relative rankings of the ions in table \(\PageIndex{1}\). Since lithium is smaller, it would take more energy to remove it, so the formation of the hydrated ion is more exothermic (negative) than the large Cesium. You must always correlate the sign of an energy to its process, and recognize that you can "form" or "break" any bond or intermolecular force. As written, this is the formation, which is the exothermic process. If you had written the reverse reaction, all the values would be positive.
Hydrated Salts: Ion-dipole forces also explain why many salts will trap water when they crystallize and form hydrated salts. This is common for small cations like sodium and lithium, which form hydrates like sodium carbonate decahydrate Na2CO3-10H2O, while larger salts like rubidium and cesium do not tend to form hydrates, as they have weaker ion-dipole interactions.
References
- Chemical Principles: Atkins and Jones
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Anonymous


