11.4: NonPolar Molecules and IMF
- Page ID
- 42006
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Van der Waals interactions are very weak short range interactions involving non-polar molecules and are inversely proportional to the 6th power of the distance of separation. There are two types of IMF involving non-polar molecules.
- Dipole-Induced Dipole: The Intermolecular forces between a polar and non-polar molecule.\[ E=-k\dfrac{\mu_1^2\alpha_2}{r^6}\]
- Instantaneous Dipole-Induced Dipole: (London Dispersive Forces) The intermolecular forces between two nonpolar molecules. \[ E=-k\dfrac{\alpha_1\alpha_2}{r^6}\]
- k is the proportionality constant (this is not Coulomb's constant, it has different units)
- r is the distance of separation between the molecules.
- \(\alpha\) is the polarizability of the non-polar molecule (see below), it has units of C m2V-1.
- \(\mu\) is the permanent dipole moment of the polar molecule.
\[ \vec{\mu} = q' \, \vec{d} \tag{11.2.3}\]
where q' is the partial charge of each end of the dipole (\(\delta ^+ or \: \delta^-\)) and d is the separation between the charges within the dipole
Polarizability (\(\alpha\))
The ease with which an electron cloud can be distorted by an electric field is its polarizability.
\[\mu_{ind} = \alpha E\]
Where
- E denotes the strength of the electric field and
- \(\alpha\) is the polarizability constant with units of C m2V-1.
All molecules are polarizable, but this is important in nonpolar symmetric molecules as it relates to how easy an external field can induce a dipole in the otherwise nonpolar molecule, and give it polar character. When an external electric field is applied it can attract electrons towards its positive pole and repulse them from its negative pole, which induces ("brings about or gives rise to") a dipole. The "tighter" the electrons are held by the molecule's nuclei the harder it is to induce a dipole, the "looser" the electrons are held, the easier it is to induce a dipole. The Polarizability (\(\alpha\)) of a molecule is a measure of the ease with which a dipole can be induced. Molecules with a large \(alpha\) are easy to induce a dipole.
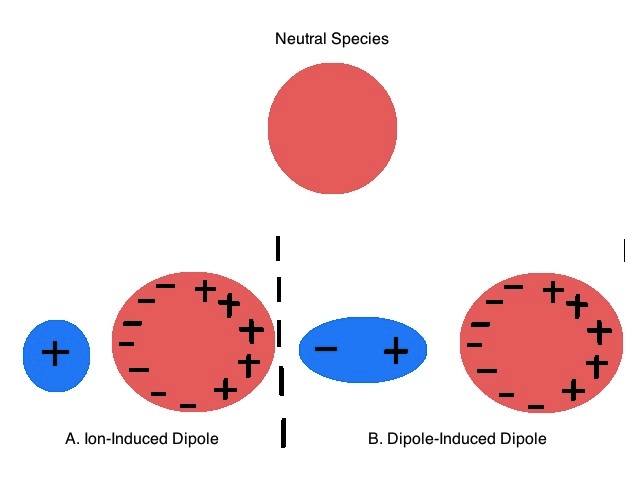
Figure \(\PageIndex{1}\): A neutral nonpolar species's electron cloud is distorted by (A.) an Ion and (B.) a polar molecule, to induce a dipole moment.
Note, \(\alpha\) has distance square in the denominator
In general, polarizability inversely correlates with the strength of the interaction between electrons and the nucleus. The tighter the valence electrons are held by the nuclei the less polarizable the molecule or atom. Conversely, well shielded valence electrons that are far from the nuclei in diffuse orbitals are highly polarizable, and easily distorted by external electric fields. In figure 11.4.1, the Electric field is coming from the (A.) positive charged ion, and (B.) the positive end of the dipole. Note, if a negative ion (or negative end of a dipole) approached a neutral molecule, the opposite would occur, as it would repel electrons, inducing a positive dipole in the neutral molecule that is near it, and a negative one that is far away.
Factors that Influence Polarizability
The relationship between polarizability and the factors of electron density and atomic radii, and molecular orientation are as follows:
- The greater the number of electrons, the greater the polarizability.
- The greater the distance of electrons from nuclear charge, the greater the polarizability of the atom.
Exercise \(\PageIndex{1}\)
Rank the noble gasses in order of increasing polarizability (least to most)
- Answer
-
He<Ne<Ar<Kr<Xe<Rn
Dipole-Induced Dipole Forces
These occur between a polar molecule and a nonpolar molecule, and thus must describe solutions. The polar molecule with a permanent dipole induces a dipole moment in the non-polar molecule. The more polarizable the nonpolar molecule, the easier it is to induce a dipole, and so the greater the interaction. .
Figure 11.4.d: Dipole (blue) inducing a dipole in an otherwise non-polar (red) molecule
\[ E=-k\dfrac{\mu_1^2\alpha_2}{r^6}\]
These are the intermolecular forces for the dissolution of many types of gases in a solvent like water. The most common gases in the atmosphere are small nonpolar compounds like nitrogen, oxygen and carbon dioxide. A saturated solution of oxygen is 256 \mu M, or 2.56x10-4 moles/l, which is an indication of how weak these intermolecular forces are. Larger and more polarizable nonpolar molecule tend to have higher solubility in polar solvents than smaller molecules of lower polarizability. We need to be careful in extrapolating trends here though, especially if the solute is not a gas, and will take a more detailed look at solutions in chapter 13, where in addition to the solute/solvent interactions described by dipole-induced dipole interactions of polar/nonpolar intermolecular interactions, we will also take into account solute/solute and solvent/solvent interactions.
Instantaneous Dipole-Induced Dipole Forces (London Dispersion Forces)
Instantaneous Dipole: A non-polar molecule like H2, O2 ,He or Ne are symmetric with their center of electron density over all time coinciding with their center of positive charge, resulting in a symmetric non-polar molecule. This symmetry is actually the time average of the molecular wavefunction, and at any instant in time the electron distribution may be asymmetric, resulting in short lived transient dipole moment. This is called an instantaneous dipole.
Induced Dipole: Just as ions and polar molecules can induce a dipole moment in an adjacent nonpolar molecule, so can an instantaneous dipole. The polarizability is a measure of how easy it is to induce a dipole. For symmetric nonpolar molecules these can form waves as successive instantaneously induced dipoles that in turn induce dipoles on their neighbors, and thus are often called dispersion forces.
London Dispersion Forces and Polarizability
The dispersion force is the weakest intermolecular force. It is an attractive force that arises from an instantaneous dipole inducing a transient dipole in an otherwise non-polar molecule. Surrounding molecules are influenced by these temporary dipole moments and a sort of chain reaction results in which subsequent weak, dipole-induced dipole interactions are created. These cumulative dipole- induced dipole interactions create the attractive dispersion forces. Dispersion forces are the forces that make nonpolar substances condense to liquids and freeze into solids when the temperature is low enough. These occur with polar molecules too, but since they are weaker, they are normally negligible.
Polarizability affects dispersion forces in the following ways:
- As polarizability increases, the dispersion forces also become stronger. Thus, molecules attract one another more vigorously and melting and boiling points of covalent substances increase with larger molecular mass and volume.
- Polarazibility also affects dispersion forces through the molecular shape of the affected molecules. Elongated molecules have electrons that are less tightly held, increasing their polarizability and thus strengthening the dispersion forces.
Exercise \(\PageIndex{2}\)
Consider two isomers of C5H10, n-pentane and neopentane (2,2-dimethylepropane). Note, isomers are different molecules with the same molecular formula (C5H10, these are called "structural isomers" because the atom connectivity is different).
 |
 |
| n-pentane | neopentane (2,2-dimethylepropane) |
(a) What are the dominant intermolecular forces for these isomers
- Answer
-
Since these are both nonpolar, they have London Dispersion or Instantaneous-Induced Dipole interactions
(b) Which has the stronger intermolecular forces and why?
- Answer
-
n-pentane is more elongated and so has a larger polarizability, and thus has stronger dispersion forces than the tighter neopentane
(c) n-pentane bp=36oC, while, neopentante bp=10oC, why are they different?
- Answer
-
n-pentane has the stronger dispersion forces, and thus requires more energy to vaporize, with the result of a higher boiling point.
Van der Waals Forces
It should be noted that short range molecular interactions with a 1/r6 distance dependency are collectively referred to as Van der Waals interactions, being named of Johannes van der Waals. These include dipole-dipole forces in the gas phase, London dispersion forces and dipole-induced dipole forces. It should also be noted that London dispersion forces occur all the time, but are often negligible compared to other forces.
 Figure \(\PageIndex{5}\): Johannes Diderik van der Waals (1837-1923), Dutch physicist and thermodynamicist who studied gasses and their condensation to liquids. (CC0: WikiMedia Commons)
Figure \(\PageIndex{5}\): Johannes Diderik van der Waals (1837-1923), Dutch physicist and thermodynamicist who studied gasses and their condensation to liquids. (CC0: WikiMedia Commons)
In van der Waals thesis he not only postulated the existence of molecules (atoms were actually still being disputed at the time), but was one of the first to postulate intermolecular forces between them, which have often been collectively lumped into "van der Waals forces". The van der Waals equation of state for gases took into account deviations from ideality due to the volume of gases and their intermolecular attractions. The size of molecules are often identified by their van der Waals radii.
Test Yourself
Query \(\PageIndex{1}\)
Query \(\PageIndex{2}\)
Sources: Chemical Principles: The Quest for Insight, 4th Ed., Atkins & Jones


