11.1: States of Matter and Intermolecular Forces
- Page ID
- 52910
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Goals
- Identify States of Matter
- Introduce concept of IMF (InterMolecular Forces) or van der Waals forces
- Introduce properties of matter that can depend on IMFs
We have learned how chemistry is the study of matter and how matter transforms from one type of "stuff" into another. We have been introduced to 4 states of matter and the next two chapters will look at the condensed phases of matter, the solid and liquid states. We are going to start with a quick review, and then move into the cohesive forces that hold matter together.
States of Matter:
- Gas State (Chapter 10)
- Compressible, variable density
- Fluid with negligible resistance to flow
- Dispersed state where matter fills entire volume of container
- negligible IMFs (InterMolecular Forces)
- Liquid State (Chapter 11)
- Incompressible, essentially constant density
- Fluid of measurable viscosity (resistance to flow)
- essentially constant density (varies slightly with temperatue)
- cohesive IMFs hold it together
- Solid State (Chapter 12)
- Incompressible, essentially constant density
- Non-Fluid, maintains own shape
- Plasma State (Chapter 1A.3.2.4, not thoroughly covered in this class)
- High Energy State (stellar matter)
- Has free electrons and charged particles

You should already be familiar with the 6 phase transitions described in figure 11.1a
- Melting: The transition from the solid to the liquid phase
- Freezing: The transition from the liquid phase to the solid phase
- Evaporating: The transition from the liquid phase to the gas phase
- Condensing:The transition from the gas phase to the liquid phase
- Sublimation: The transition from the solid phase to the gas phase
- Deposition: The transition from the gas phase to the solid phase
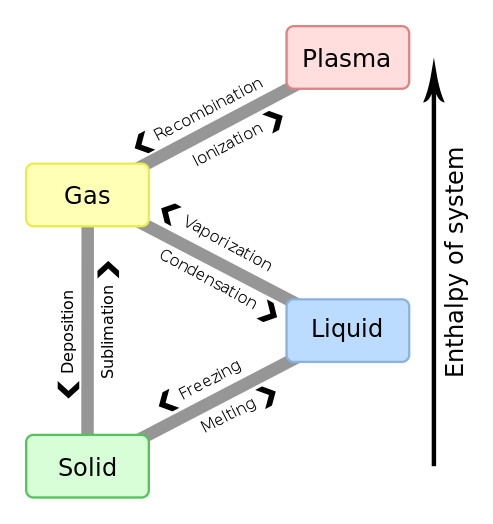
Fig. 11.1b: Four states of matter with transitions between them.
Intermolecular Forces (IMF)
The the term InterMolecular Force (IMF) literally means the forces between molecules, and as such, is often a misnomer, as simply speaking, not all matter is composed of molecules. Yet this term is used pervasively, and so we will use it, but first lets compare it to the so called "intramolecular forces", the forces within the proverbial "molecule." We typically consider two types of bonds, ionic (which are not molecular) and covalent (which are molecular). So if I have liquid water, where the discrete entity of matter is the H2O molecule, there are two type of bonds, those between H and O of a water molecule (covalent intramolecular) and those between the H of one molecule and the O of another (intermolecular).
Shortcomings of the term Intermolecular
- We classify bonds between an ion and polar molecule as intermolecular, when in reality, the ion need not be a molecule (polyatomic ions are molecules, monatomic ions are not).
- Not all covalently bonded compounds are molecules with discrete formula, like diamond, which is a covalent network, and so even though it is a covalently bonded entity, it does not fit the paradigm of a molecule with a unique molecular formula.
With these shortcomings in mind we are going to look at the following types of Intermolecular Forces. It should also be noted that the later types of forces are also called van der Waals forces, which are the short range forces of attraction between atoms or molecules that do not fit into the model of a covalent or ionic bond.
Types of Intermolecular Forces
- Ion-Dipole Forces (these may not be true IMF, but we will call them IMFs)
- Solutions
- Dipole-Dipole Forces (between two polar molecules)
- Pure substance or solutions
- Hydrogen Bonding (special type of dipole-dipole)
- Pure substance or solutions
- Dipole-Induced Dipole (between polar and nonpolar molecules)
- Solutions
- Instantaneous Dipole-Induced Dipole (between two nonpolar molecules, often called London Dispersion Forces)
- Solutions or Pure Substances
Please note that in recognizing what type of intermolecular forces are involved we need to know if a molecule is polar or non-polar. This requires a review of Lewis Dot Structures, VSEPR Theory, Electronegativety, and Bond Polarity.
Properties of Matter that Depend on IMFs
- boiling point, melting point, stable phases
- enthalpies of phase transitions
- vapor pressure
- solubility and miscibility of different substances
- viscosity
There are many physical properties of matter that are strongly influenced by IMFs, and over the next few chapters we will look at many of these. Lets ask a simple question;
Exercise \(\PageIndex{1}\)
At a given temperature, would it be easier to vaporize a light molecule or a heavy molecule?
- Answer
-
You need more information. From our study of gases and the Kinetic Molecular Theory we learned that the average kinetic energy of a molecular system is proportional to the absolute temperature, and both molecules have the same average kinetic energy, and so at first thought, we would predict that the lighter molecule would tend to have the higher velocity (review Graham's Law of Effusion) and be easier to vaporize (see image below).
The problem is we need to identify the intermolecular forces that attract the molecules to each other, and if the lighter molecule had stronger intermolecular forces, this would be wrong. Look at the case of carbon dioxide and water (the next question deals with this).
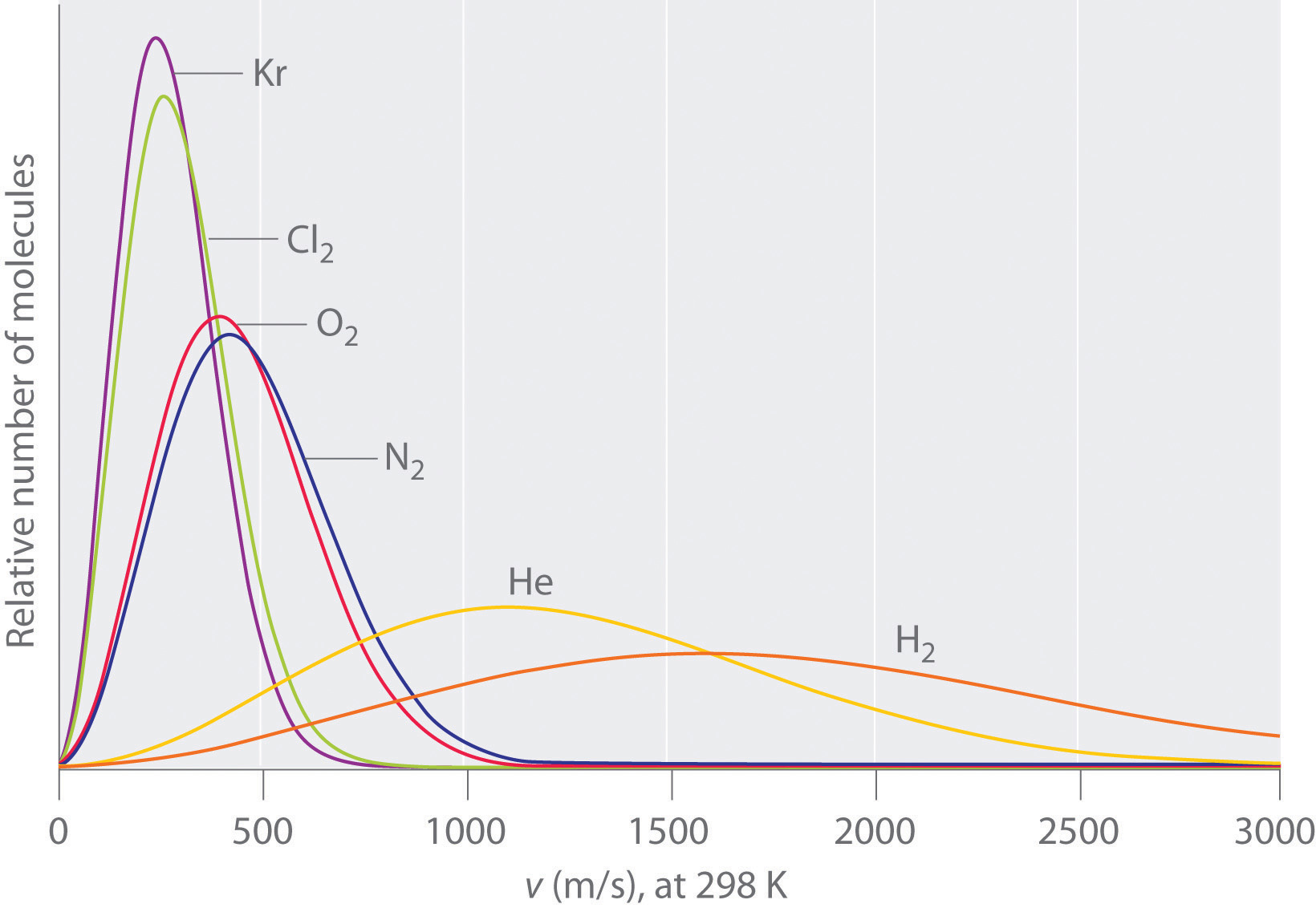
Note: This image is for the velocity distribution of a gas at a given temperature, and not a liquid, but the concept is valid, in that if all other things are equal, lighter molecules tend to move faster, and gas phase systems move faster than liquid. The problem is, there are often other factors, as indicated in the next question, on why is carbon dioxide a gas at ambient questions while water is a liquid?
Exercise \(\PageIndex{2}\)
So why at ambient conditions is Carbon Dioxide (the heavier molecule at 44 amu) a gas, but water (the lighter molecule at 18 amu) is a liquid?
- Answer
- That is, shouldn't it be easier to vaporize the lighter molecule than the heavier one? The answer lies within the Intermolecular Forces, and if you review molecular shapes and polarity you will see that water is a polar molecule while carbon dioxide is non-polar, and this leads to different physical properties like the boiling and melting points. That is, in this chapter you will learn that water has stronger intermolecular forces than carbon dioxide, and that is why it is a liquid, while carbon dioxide is a gas. But to answer that question you first had to determine the Lewis Dot Structure, then determine the geometry, and then determine the polarity of the molecule, and so you should have a basic understanding of that pre-requisite material before proceeding.
Another interesting things to note about molecular properties that result from IMFs is that they are not really properties of a single molecule, but the result of an ensemble or large system of many molecules, which must be viewed as a whole, and not as individual molecules. Simple speaking, an individual molecule can not have a boiling point, which is really a function of the interaction between a large number of molecules. So the boiling point of water is not a property of a water molecule, but a bunch of water molecules. So, if you have a liquid at a given temperature there is a distribution of velocities, some of the molecules have enough kinetic energy to escape the attractive cohesive forces on the surface and enter the vapor phase, while others do not. So the vapor pressure above a liquid is also influenced by intermolecular forces. The point is some properties of a substance, like it's atomic mass or its polarity, are the property of a single molecule, while others, like the melting point or vapor pressure, are the properties of a huge number (ensemble) of molecules


