8.1.3: Magnetic Properties of Coordination Compounds
- Page ID
- 60906
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Experimental evidence of magnetic measurements supports the theory of high- and low-spin complexes. Remember that molecules such as O2 that contain unpaired electrons are paramagnetic. Paramagnetic substances are attracted to magnetic fields. (see video)
Many transition metal complexes have unpaired electrons and hence are paramagnetic. Molecules such as N2 and ions such as Na+ and [Fe(CN)6]4− that contain no unpaired electrons are diamagnetic. Diamagnetic substances have a slight tendency to be repelled by magnetic fields.
When an electron in an atom or ion is unpaired, the magnetic moment due to its spin makes the entire atom or ion paramagnetic. The size of the magnetic moment of a system containing unpaired electrons is directly related to the number of such electrons: the greater the number of unpaired electrons, the larger the magnetic moment. Magnetic susceptibility measures the force experienced by a substance in a magnetic field. When we compare the weight of a sample to the weight measured in a magnetic field (Figure \(\PageIndex{1}\)), paramagnetic samples that are attracted to the magnet will appear heavier because of the force exerted by the magnetic field. We can calculate the number of unpaired electrons based on the increase in weight.
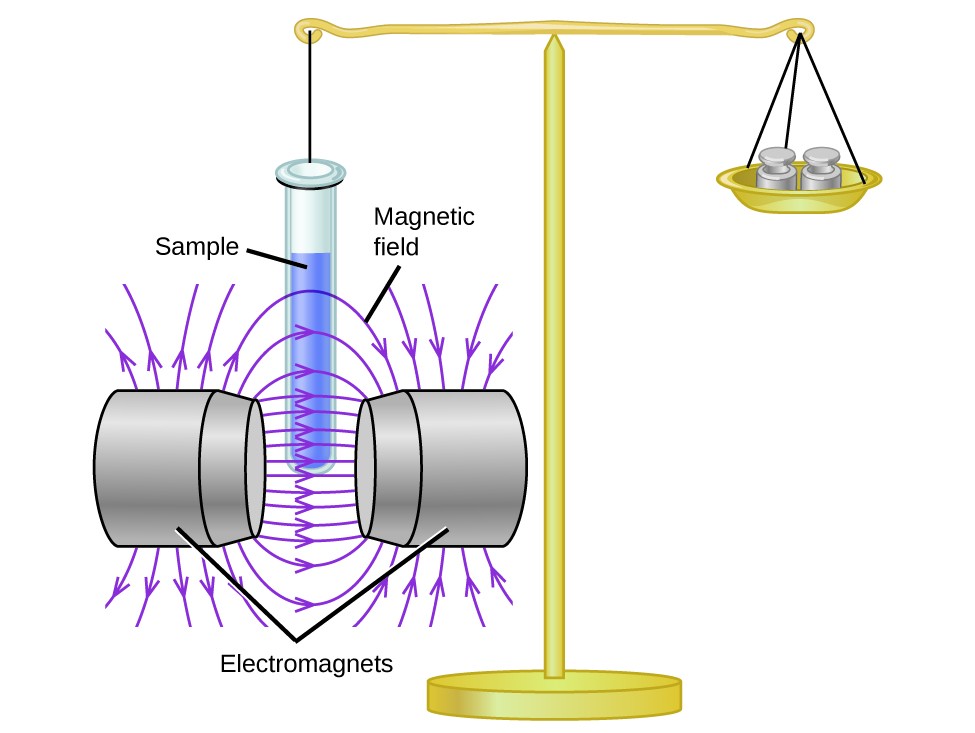
\(\PageIndex{1}\): A Gouy balance compares the mass of a sample in the presence of a magnetic field with the mass with the electromagnet turned off to determine the number of unpaired electrons in a sample. (CC BY-SA 3.0; OpenStax).
From this experiment, the measured magnetic moment of low-spin d6 [Fe(CN)6]4− ion confirms that iron is diamagnetic, whereas the high-spin d6 [Fe(H2O)6]2+ complex has four unpaired electrons with a magnetic moment that confirms this arrangement. Therefore, the observed magnetic moment is used to determine the number of unpaired electrons present.
Magnetic Properties of Coordination Compounds
An interesting characteristic of transition metals is their ability to form magnets. Metal complexes that have unpaired electrons are magnetic. Since the last electrons reside in the d orbitals, this magnetism must result from unpaired d electrons. Considering only monometallic complexes, unpaired electrons arise because the complex has an odd number of electrons or because electron pairing is destabilized. For example, the Ti(III) ion has one d electron and must be (weakly) paramagnetic, regardless of the geometry or the nature of the ligands. However, the Ti(II) ion with two d-electrons, sometimes forms complexes with two unpaired electrons and sometimes forms complexes with no unpaired electrons.
As an example, Fe3+ has five d electrons prefers octahedral geometry. The complex [FeF6]3- is high-spin \(d^5\) and is attracted strongly to magnetic fields; however, \([Fe(CN)_6]^{3-}\) is low-spin \(d^5\) and only has one unpaired electron, making it a weaker magnet. This trend can be explained based on the properties of the ligands.
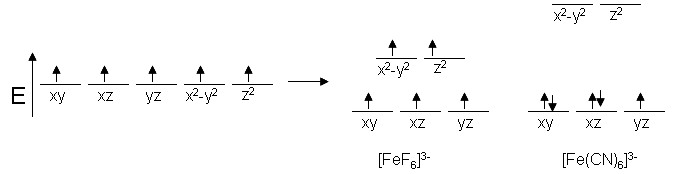
\(\PageIndex{2}\): Crystal field theory splitting diagram. Example of influence of ligand electronic properties on d orbital splitting. This shows the comparison of low-spin versus high-spin electrons.
Which one of the following coordination compounds would you expect to be paramagnetic?
- \([Zn(NH_3)_4]Cl_2\)
- \(K[FeCl_4]\)
- \([Cd(H_2O)_6]SO_4\)
Solution
Let's consider each compound individually. Since each compound has only one complex ion, we only need to consider how the d electrons are distributed in the ligand field of that ion. We can ignore the other parts (the counter ions) of the compound.
- The zinc ion in \([Zn(NH_3)_4]Cl_2\) has a +2 oxidation state and is a d10. This is a diamagnetic compound.
- The iron ion in \(K[FeCl_4]\) has a +3 oxidation state and is d5. It only has four electrons and is more likely to be in a tetrahedral geometry than square planar. For tetrahedral geometries, we expect high spin; further, it has weak-field ligands. This compound will be paramagnetic (with five unpaired electrons).
- The cadmium ion in \([Cd(H_2O)_6]SO_4\) has a +2 oxidation state, and is d10. This is a diamagnetic compound.
Predict the number of unpaired electrons for each of the following complex ions, and tell whether it will be attracted or repelled by a magnetic field.
- \([Fe(CN)_6]^{4‐} \)
- \([Ru(NH_3)_6]^{3+} \)
- \([Cr(NH_3)_6]^{2+} \)
- Answer
-
- \(Fe^{2+}\): a 3d6 ion bound to strong field ligands; thus we expect low spin and 0 unpaired electrons. This diamagnetic compound will be repelled by a magnetic field.
- \(Ru^{3+}\): a 4d5 ion; thus we expect low spin with 1 unpaired electron. This paramagnetic compound will be weakly attracted to a magnetic field.
- \(Cr^{2+}\): a 3d4 ion bound to weak field ligands; thus we expect high spin and 4 unpaired electrons. This paramagnetic complex will be strongly attracted to a magnetic field.
In bi- and polymetallic complexes, in which the individual centers have an odd number of electrons or electrons are high-spin, the situation is more complicated. If there is interaction between the two (or more) metal centers, the electrons may couple, resulting in a weak magnet, or they may enhance each other. When there is no interaction, the two (or more) individual metal centers behave as if they are in two separate molecules.
Contributors and Attributions
- Source: Boundless. "Magnetic Properties." Boundless Chemistry Boundless, 26 May. 2016. Retrieved 4 May. 2017 from https://www.boundless.com/chemistry/...ties-616-6882/.
Curated or created by Kathryn Haas

