8.1.1: Colors of Coordination Compounds (Electronic Absorption Spectra)
- Page ID
- 60909
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The d-orbital splitting in coordination complexes results in a gap (\(\Delta\)) that happens to be just the right magnitude to absorb visible light. Because metal complexes can absorb visible light, the display an array of colors. Not only is the color attractive to the eye, it is an indication of the chemical and physical properties of the metal complex. The color (like the magnitude of \(\Delta\)) depends on the identity of the metal ion, the coordination geometry, and the ligand identity. Chemists don't just "look" at color, though - we measure it using a UV-visible spectrometer.
An example of such a measurement is shown below in Figure \(\PageIndex{1}\) for a Cu(II) complex. The sample appears a pinky-purple color to the eye, and when it is measured using a UV-visible spectrometer, it is shown to absorb visible light at 525 nm. The absorption spectrum can tell us a lot about which ligands are bound to the Cu(II) ion and what the coordination geometry is. This example might be familiar to you if you've had Advanced Lab with Dr. Haas!
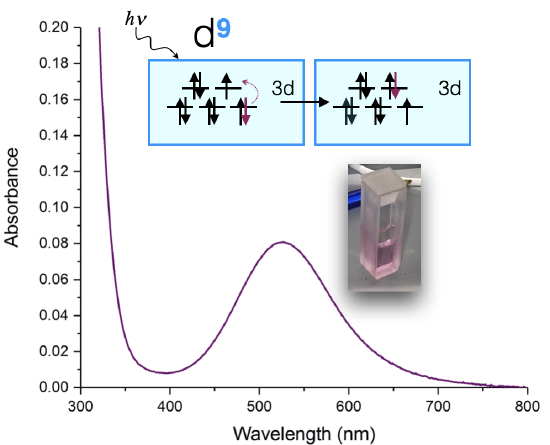
In some ways this is a "simple" spectrum because it has only one visible-light d-d transition at 525 nm. Let's assume that the coordination geometry is approximately octahedral (although it is actually a Jhan-Teller distorted octahedron, and more like a square plane). If we assume it's octahedral, then the d-orbital splitting diagram might lead us to expect one transition: an electron from the \(t_{2g}\) is excited to \(e_g\). We might expect then, that the energy absorbed is equal to the energy of the \(\Delta_o\). However, the actual energy of the transition is also effected by electron-electron repulsion energies, and so it is not quite so simple.
If we would want to determine \(\Delta_o\) from the spectrum shown in Figure \(\PageIndex{1}\), we need to use Tanabe-Sugano diagrams, which account for electronelectron repulsions, to extract the value of \(\Delta_o\). An objective in the next Unit is to learn use Tanabe-Sugano diagrams to extract \(\Delta\) values and assign the specific electronic transitions that result in UV-vis spectra. But first, let's remind ourselves of where color comes from and learn the basics of how this applies to transition metal complexes.
The Electromagnetic Spectrum
The electromagnetic spectrum (EM) spectrum is made up of photons of different wavelengths. Photons, unique in displaying the properties of both waves and particles, create visible light and colors in a small portion of the EM spectrum. This visible light portion has wavelengths in approximately the 400-700 nanometer range (a nanometer, “nm,” is 10-9 meters). Each specific wavelength corresponds to a different color (Figure \(\PageIndex{2}\)), and when all the wavelengths are present, it appears as white light.

The wavelength (\(\lambda\)) and frequency (\(\nu\)) of a wave are inversely proportional: as one increases, the other decreases; this is a consequence of all light traveling at the same speed. \[\lambda = \nu^{-1}\] Because of this relationship, blue light has a shorter wavelength, higher frequency, more energy than red light. In general, photons to the right of the EM spectrum have increasingly higher energy than photons to the left.
Perceiving Color
Color is perceived in two ways, through additive mixing, where different colors are made by combining different colors of light, and through subtractive mixing, where different wavelengths of light are taken out so that the light is no longer pure white. For colors of coordination complexes, subtractive mixing is considered. As shown in Figure \(\PageIndex{3}\), the idea behind subtractive mixing is that white light (which is made from all the colors mixed together) interacts with an object. The object absorbs some of the light, and then reflects or transmits (or both, depending on the object) the rest of the light, which contacts the eye. The object is perceived as whichever color is not absorbed. In Figure \(\PageIndex{2}\), white light (simplified as blue, green, yellow, orange, and red squiggly arrows) is shone through a solution. The solution absorbs the yellow wavelengths; other wavelengths are transmitted and the appears a pinky-purple color.

This phenomenon takes place whenever an object displays visible color. If none of the light is absorbed, and all is reflected back off, the object appears white; if all of the light is absorbed, and there is none left to reflect or transmit through, the object appears black.
Colors of metal complexes (d-d transitions)
In the case of an octahedral metal complex, as certain wavelengths of visible light are absorbed, subtractive color mixing occurs and the coordination complex solution appears colored. If there is no electronic transition (eg a \(d^{10}\) complex), the solutions appear colorless; in reality, they still have a measured energy and absorb certain wavelengths of light, but these wavelengths are not in the visible portion of the EM spectrum and no color is perceived by the eye.
In general, a larger \(∆_o\) indicates that higher energy photons are absorbed, and the solution appears further to the left on the EM spectrum shown in Figure \(\PageIndex{1}\). This relationship is described in the equation
\[∆_o \approx hc/λ\]
where \(h\) and \(c\) are constants, and \(λ\) is the wavelength of light absorbed. The "\(\approx\) symbol is used to indicate that this relationship is only approximate. As mentioned earlier, changes in electron-electron repulsion energies must also be accounted for.
Determining color
Using a color wheel can be useful for determining what color a solution will appear based on what wavelengths it absorbs (Figure \(\PageIndex{4}\)). If a complex absorbs a particular color, it will have the appearance of whatever color is directly opposite it on the wheel. For example, if a complex is known to absorb photons in the orange range, it can be concluded that the solution will look blue. This concept can be used in reverse to determine ∆ for a complex from the color of its solution.

Relating the Colors of Coordination Complexes to the Spectrochemical Series
A description of the spectrochemical series is available in a previous section. Weaker-field ligands contribute to smaller \(\Delta\) values, and thus absorbance of lower-energy light with longer (\lambda\) (ie a "red shift"). Stronger-field ligands do the opposite; they contribute to larger magnitude of \(\Delta\) and absorbance of higher-energy light with shorter \(\lambda\) (ie a "blue shift").
If a solution with a dissolved octahedral complex appears yellow to the eye, approximately what wavelength/color of light does it absorb? If the "borderline" between high and low spin complexes is roughly around 588 nm, is this complex expected to be low spin or high spin?
Solution
A solution that looks yellow absorbs light that is violet, which is roughly 410 nm from the color wheel. This is higher-energy than 588 nm, and so this complex must have a rather large \(\Delta\); at least large enough to expect low spin.
An octahedral metal complex absorbs light with wavelength 535 nm. What is the crystal field splitting \(\Delta_o\) for the complex? Approximately what color is it to the eye?
Solution
To solve this question, we need to use the equation \(\Delta_o \approx \dfrac{hc}{\lambda} \nonumber\)
with
- \(h\) is Planck’s constant and is \(6.625 \times 10^{-34} J \cdot s\) and
- \(c\) is the speed of light and is \(2.998 \times 10^8\, m/s\).
It is also important to remember that 1 nm is equal to \(1 \times 10^{-9}\) meters. With all this information, the final equation looks like this:
\[\Delta_o \approx \dfrac{(6.625 \times 10^{-34}\, J \cdot s)(2.998 \times 10^8\, m/s)}{(535nm) \left(\dfrac{1\,m}{1 \times 10^9\, nm}\right)}= 3.712 \,J/molecule \nonumber\]
It is not necessary to use any equations to solve the second part of the problem. Light that is 535 nm is green, and because green light is absorbed, the complex appears redish (light red is pink) (refer to Figures \(\PageIndex{2}\) and \(\PageIndex{4}\) for this information).
Note: the fact that the complex is octahedral makes no impact when solving this problem. Although the splitting is different for complexes of different structures, the mechanics of solving the problem are identical.
There are two solutions, one orange and one blue. Both solutions are known to be made up of a cobalt complex; however, one has chloride ligands, while the other has ammonia ligands. Which solution is expected to be orange?
Solution
In order to solve this problem, it is necessary to know the relative field-strengths of the ligands involved. NH3 is a stronger-field ligand than Cl-, which means that the complex involving NH3 has a greater \(\Delta_o\). Because of the larger ∆, the electrons absorb higher-energy light, and the solution will have the appearance of a lower energy (more red) color. Since orange light is less energetic than blue light, the orange solution is the cobalt complex with \(\ce{NH3}\) ligands.
References
- Cox, P. A. Instant Notes Inorganic Chemistry. Second ed. Grand Rapids: Garland, Incorporated, 2004.
- Nassau, Kurt. The Physics and Chemistry of Color : The Fifteen Causes of Color. Second ed. New York: Wiley-Interscience, 2001.
- Petrucci, Ralph H., William S. Harwood, and Geoff E. Herring. General Chemistry : Principles and Modern Applications. Ninth ed. Upper Saddle River: Prentice Hall PTR, 2006.
- Petrucci, Ralph H., Carey Bissonnette, F. Geoffrey Herring, Jeffrey D. Madura. General Chemistry: Principles and Modern Applications. Tenth Ed. Upper Saddle River: Pearson Education, Inc. 2011.
Problems
- What color will a complex be that absorbs light that is 600 nm be?
- What color will a complex an octahedral complex appear if it has a \(\Delta_o\) of \(3.75 \times 10^{-19}\, J\)?
- Would you expect a green coordination complex to be high spin or low spin? What about a yellow complex?
- There are two solutions, one which is yellow and another which is violet. The solutions are [Co(H2O)6]3+and [Co(CN-)6]3-. What are the colors of each solution?
Answers
- Blue. The color absorbed is orange.
- It is red. Using Δ=hc/λ, h=6.626*10-34J*s, c=2.998*108m/s, wavelength would equal 530 nm. So green is absorbed, and the complementary color of green is red, so red is the color of the complex.
- We were told in a previous exercise that the "line" between high and low spin is approximately 580 nm.
Green Complex: The complementary color of green is red, which has \(\lambda \approx 420\) nm. The green solution has a rather small \(\Delta\) and we could expect it to be high-spin.
Yellow complex: The complementary color of yellow is violet, absorbed is green, which has \(\lambda \approx 700\) nm. The yellow complex has a rather large \(\Delta_o\) and thus we could expect a low-spin complex. - [Co(H2O)6]3+ is violet and [Co(CN-)6]3- is yellow. Looking at the spectrochemical series, H2O is a weak-field ligand, so it absorbs colors of long wavelengths—in this case, the longer wavelength is yellow, so the color reflected is violet. CN- is a strong-field ligand, so it absorbs colors of shorter wavelengths-in this case, the shorter wavelength is violet, so the color reflected is yellow.
Contributors and Attributions
- Deyu Wang (UCD)
Curated or created by Kathryn Haas

