3.3.3: Molecular Orbitals - Homonuclear Diatomic Molecules
- Page ID
- 202267
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sigma Bonding with s-orbitals (ex: Dihydrogen)
In the case of the hydrogen molecule, we took two atomic orbitals and combined them to form two molecular orbitals. These new molecular orbitals had different wavelengths than the two atomic orbitals: one had a longer wavelength and was a little lower in energy, while the other had a shorter wavelength and was a little higher in energy. If we take into account the energy of the two original atomic wavefunctions, and compare them to the total energy of the two new molecular wavefunctions, there is no change overall.
We started with two atomic orbitals, and by combining them we produced two molecular orbitals. Both of these ideas are useful in considering the formation of more complex molecules from individual atoms.
-
- The average energy of the orbitals has remained almost constant.
- Also, the number of wavefunctions has remained constant.
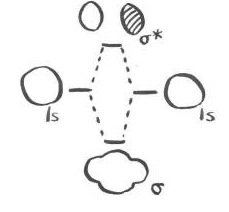
Of course, from the point of view of the two real electrons, some remarkable changes have occurred. Both of these electrons have adopted a longer wavelength and a lower energy and that has made all the difference. There is an occupied molecular orbital and an unoccupied molecular orbital; only the occupied orbital makes a real energetic contribution to the overall stability of the molecule. The unoccupied orbital is completely imaginary.
A bonding picture of He2 would look exactly the same, because it would also involve the overlap of 1s electrons on one atom with 1s electrons on the other atom. There would be a different electronic energy, however. That difference would affect the prospects of helium-helium bond formation.
- The electrons have lower kinetic energy in the bond than they had before bonding.
- Electronic energy has decreased. A stable bond has formed.
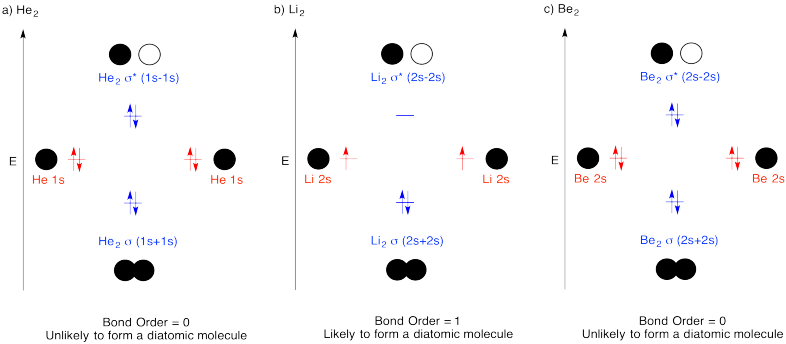
Construct molecular orbital diagrams for the following diatomic species and discuss the likelihood of bond formation in each case.
- He2.
- Li2.
- Be2.
- Answer
-
Bonding with P-orbitals
Sigma bonding with p-orbitals
Other diatomic molecules in the upper right corner of the periodic table can be constructed in a similar way. Look at dinitrogen, N2.
We can think about how dinitrogen would form if two nitrogen atoms were placed close enough together to share electrons. Nitrogen has more electrons than hydrogen, so this interaction is more complicated.
In our qualitative examination of bonding in main group diatomics, we will take the approach used in Lewis structures and just look at the valence electrons. A quantitative molecular orbital calculation with a computer would not take this shortcut, but would include all of the electrons in the atoms that are bonding together.
Nitrogen has five valence electrons, and these electrons are found in the 2s and 2p levels. There are three possible atomic orbitals in the 2p level where some of these electrons could be found: px, py and pz. We need to look at the interaction between the s and px, py and pz orbitals on one nitrogen atom with the s and px, py and pz orbitals on the other nitrogen. That process could be extremely complicated, but:
- Orbital interactions are governed by symmetry.
Orbitals interact most easily with other orbitals that have the same element of symmetry. For now, we can simplify and say that orbitals on one atom only interact with the same type of orbitals on the other atom.
- s orbitals interact with s orbitals. We can already see how that will work out in dinitrogen, because that is what happened in dihydrogen.
- px orbitals interact with px orbitals.
- py orbitals interact with py orbitals.
- pz orbitals interact with pz orbitals.
Another complication here is that the s and p orbitals do not start out at the same energy level. When the orbitals mix, one combination goes up in energy and one goes down. Does the s antibonding combination go higher in energy than the combinations from p orbitals? Do the p bonding combinations go lower in energy than the combinations from s orbitals? We will simplify and assume that the s and p levels remain completely separate from each other. This is not always true, but the situation varies depending on what atoms we are dealing with.
- The combination of one s orbital with another is just like in hydrogen. Two original orbitals will combine and rearrange to produce two new orbitals.
- There is a bonding combination in which the orbitals are in phase. The new orbital produced has a longer wavelength than the original orbital. It is lower in energy.
- There is an antibonding combination in which the orbitals are out of phase. The new orbital produced has a shorter wavelength than the original orbital. It is higher in energy.
In considering the interaction of two p orbitals, we have to keep in mind that p orbitals are directional. A p orbital lies along a particular axis: x, y or z. The three p orbitals on nitrogen are all mutually perpendicular (or orthogonal) to each other. That situation is in contrast to s orbitals, which are spherical and thus look the same from any direction.
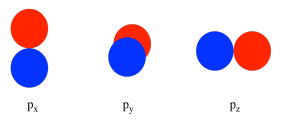
We first need to define one axis as lying along the N-N bond. It does not really matter which one. We arbitrarily say the N-N bond lies along the z axis. The pz orbitals have a different spatial relationship to each other compared to the py and px. The pz orbitals lie along the bond axis, whereas the py and px are orthogonal to it.

As the nitrogen atoms are brought together, one lobe on one pz orbital overlaps strongly with one lobe on the other pz orbital. The other lobes point away from each other and do not interact in any obvious way.
As with the s orbital, the pz orbitals can be in-phase or out-of-phase. The in-phase combination results in constructive interference. (Here, "in-phase" means the lobes that overlap are in-phase; for that to happen the two p orbitals are actually completely out-of-phase with each other mathematically, so that one orbital is the mirror image of the other.) This combination is at a longer wavelength than the original orbital. It is a lower energy combination.
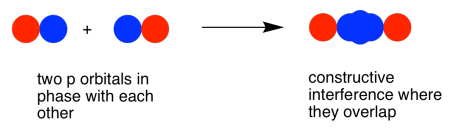
The out-of-phase combination (meaning in this case that the overlapping lobes are out-of-phase) results in destructive interference. This combination is at shorter wavelength than the original orbital. It is a higher energy combination.
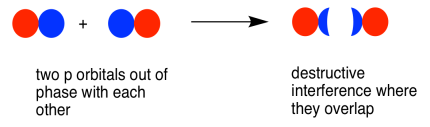
As a result, we have two different combinations stemming from two different p orbitals coming together in two different ways. We get a low-energy, in-phase, bonding combination and a high-energy, out-of-phase, antibonding combination.
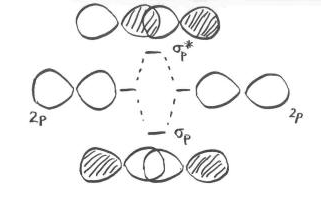
What about those other p orbitals, the ones that do not lie along the bond axis? We'll take a look at that problem on the next page.
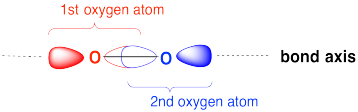
Draw an MO cartoon of a sigma bonding orbital formed by the overlap of two p orbitals between two oxygen atoms. Label the positions of the oxygen nuclei with the symbol "O". Label the O-O bond axis.
- Answer
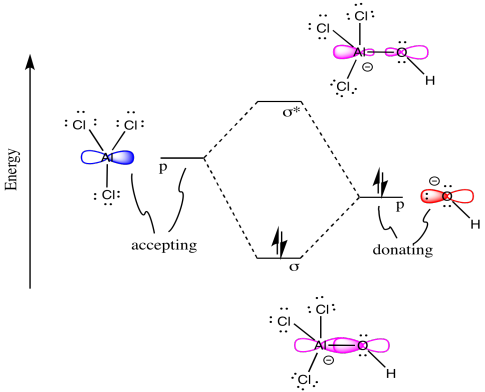
Chemical reactions can be described by MO diagrams too! Consider the following reaction in which a new sigma bond is formed.

Draw an MO diagram for the reaction above. In other words, start from the one frontier MO on each reactant to build the MO's of the new sigma bond in the product.
o Draw the orbital from the base (hydroxide) that is likely to donate its electrons.
o Draw the orbital from the acid (aluminum chloride) that is likely to accept electrons.
o Complete the MO mixing diagram of these two orbitals:
• Label the electron donating orbital
• Label the electron accepting orbital
• Populate the MO mixing diagram with electrons
o Draw a cartoon showing each reactant and product MO that contributes to the bonding interaction.
- Answer
Pi-bonding with p-orbitals
Earlier, we saw that p orbitals that lie along the same axis can interact to form bonds.
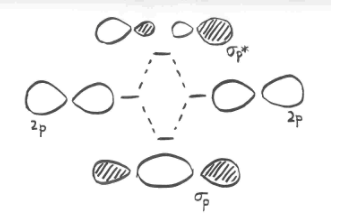
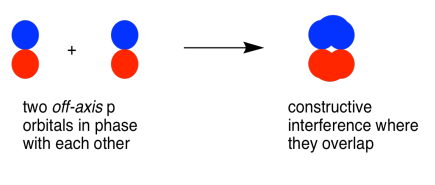
Parallel, but not collinear, p orbitals can also interact with each other. They would approach each other side by side, above and below the bond axis between the two atoms. They can be close enough to each other to overlap, although they do not overlap as strongly as orbitals lying along the bond axis. They can make an in-phase combination, as shown below.
They could also make an out-of-phase combination, as shown below.
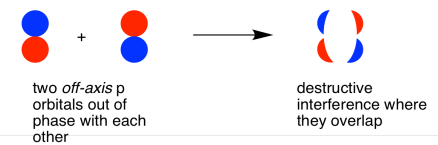
- parallel p orbitals can overlap to produce bonding and antibonding combinations.
- the resulting orbitals contain nodes along the bond axis.
- the electron density is found above and below the bond axis.
- this is called a p (pi) bond.
The illustration above is for one set of p orbitals that are orthogonal to the bond axis. The second picture shows the result of the constructive (or destructive) interference. A similar picture could be shown for the other set of p orbitals.
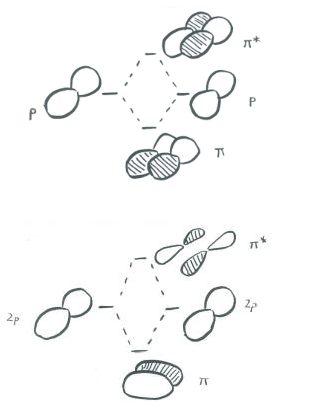
In a main group diatomic species like dinitrogen, one p orbital lying along the bond axis can engage in s bonding. The two p orbitals orthogonal to the bond axis can engage in p bonding. There will be both bonding and antibonding combinations.
Just as the sigma-bonding orbitals display progressively shorter wavelengths along the bonding axis as they go to higher energy, so do the pi bonding orbitals. In other words, there are more nodes in the higher-energy orbitals than in the lower-energy ones.
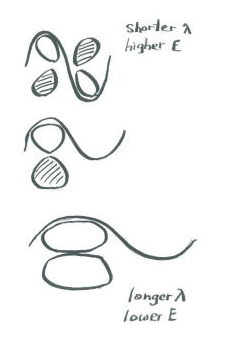
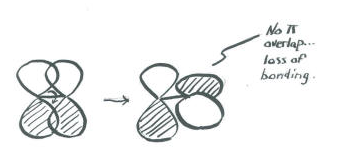
An important consequence of the spatial distribution or "shape" of a p orbital is that it is not symmetric with respect to the bond axis. An s orbital is not affected when the atom at one end of the bond is rotated with respect to the other. A p orbital is affected by such a rotation. If one atom turns with respect to the other, the p orbital would have to stretch to maintain the connection. The orbitals would not be able to overlap, so the connection between the atoms would be lost.
The combinations of ______________ atomic orbitals leads to σ orbitals.
Draw pictures.
- Answer
-
The combinations of s + s OR s + p OR p + p OR s + d OR p + d atomic orbitals can lead to σ orbitals.
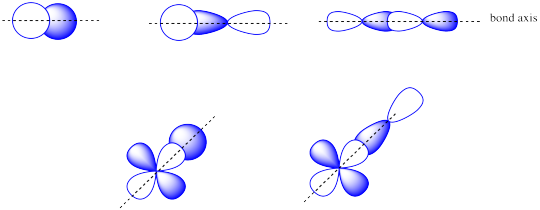
The combinations of ______________ atomic orbitals leads to π orbitals.
Draw pictures.
- Answer
-
The combinations of side by side p + p or p + d atomic orbitals leads to π orbitals.

Which molecular orbital is typically the highest in energy?
a. p
b. σ
c. π*
d. π
e. σ*
- Answer
-
e) σ*
Why would a core 1s orbital not interact with a valence 2s orbital?
Hint: Why is a Li2O bond stronger than a K2O bond?
- Answer
-
Li+ and O2- are more similar in size than K+ and O2-, so the bond between Li+ and O2- is stronger.
The energy difference between any core orbitals and valence orbitals is too large, so they cannot interact. In order for orbitals to interact, the orbitals need to have the same symmetry, be in the same plane, and be similar in energy.
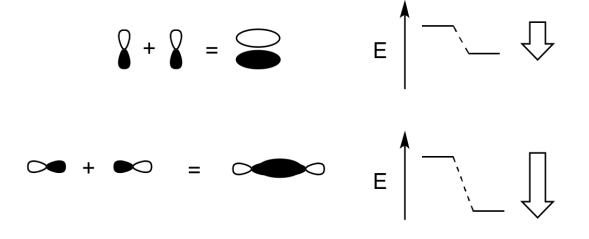
Add a few words to explain the ideas conveyed in these drawings.
- Answer
-
When two parallel p orbitals combine out-of-phase, destructive interference occurs.
There is a node between the atoms.
The energy of the electrons increases.
When two parallel p orbitals combine in-phase, constructive interference occurs.
There is no node between the atoms; the electrons are found above and below the axis connecting the atoms.
The energy of the electrons decreases.
Attribution
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)
Curated or created by Kathryn Haas

