B. Other Geometries
- Page ID
- 59602
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Description of d-Orbitals
To understand CFT, one must understand the description of the lobes:
- dxy: lobes lie in-between the x and the y axes.
- dxz: lobes lie in-between the x and the z axes.
- dyz: lobes lie in-between the y and the z axes.
- dx2-y2: lobes lie on the x and y axes.
- dz2: there are two lobes on the z axes and there is a donut shape ring that lies on the xy plane around the other two lobes.
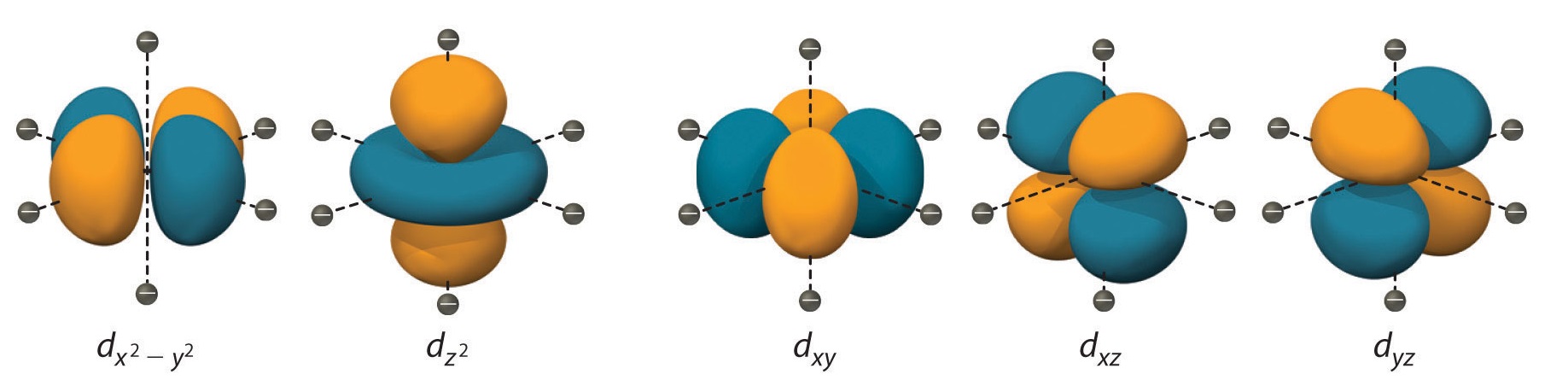
Figure 3: Spatial arrangement of ligands in the an octahedral ligand field with respect to the five d-orbitals.
Octahedral Complexes
In an octahedral complex, there are six ligands attached to the central transition metal. The d-orbital splits into two different levels. The bottom three energy levels are named \(d_{xy}\), \(d_{xz}\), and \(d_{yz}\) (collectively referred to as \(t_{2g}\)). The two upper energy levels are named \(d_{x^²-y^²}\), and \(d_{z^²}\) (collectively referred to as \(e_g\)).
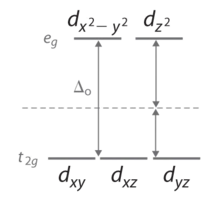
Figure 4: Splitting of the degenerate d-orbitals (without a ligand field) due to an octahedral ligand field shown in Figure 3.
The reason they split is because of the electrostatic interactions between the electrons of the ligand and the lobes of the d-orbital. In an octahedral, the electrons are attracted to the axes. Any orbital that has a lobe on the axes moves to a higher energy level. This means that in an octahedral, the energy levels of \(e_g\) are higher (0.6∆o) while \(t_{2g}\) is lower (0.4∆o). The distance that the electrons have to move from \(t_{2g}\) from \(e_g\) and it dictates the energy that the complex will absorb from white light, which will determine the color. Whether the complex is paramagnetic or diamagnetic will be determined by the spin state. If there are unpaired electrons, the complex is paramagnetic; if all electrons are paired, the complex is diamagnetic.
Tetrahedral Complexes
In a tetrahedral complex, there are four ligands attached to the central metal. The d orbitals also split into two different energy levels. The top three consist of the \(d_{xy}\), \(d_{xz}\), and \(d_{yz}\) orbitals. The bottom two consist of the \(d_{x^2-y^2}\) and \(d_{z^2}\) orbitals. The reason for this is due to poor orbital overlap between the metal and the ligand orbitals. The orbitals are directed on the axes, while the ligands are not.
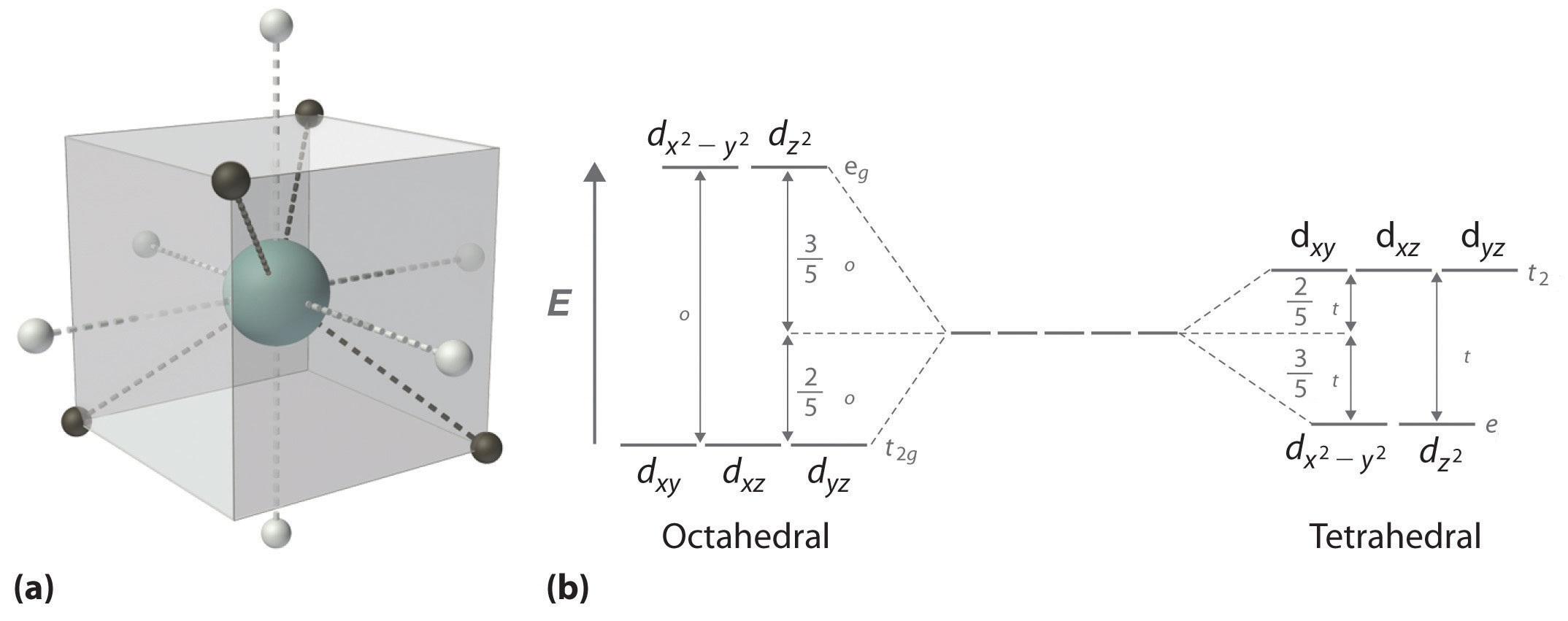
Figure 5: (a) Tetraheral ligand field surrounding a central transition metal (blue sphere). (b) Splitting of the degenerate d-orbitals (without a ligand field) due to an octahedral ligand field (left diagram) and the tetrahedral field (right diagram).
The difference in the splitting energy is tetrahedral splitting constant (\(\Delta_{t}\)), which less than (\(\Delta_{o}\)) for the same ligands:
\[\Delta_{t} = 0.44\,\Delta_o \tag{1}\]
Consequentially, \(\Delta_{t}\) is typically smaller than the spin pairing energy, so tetrahedral complexes are usually high spin.
Square Planar Complexes
In a square planar, there are four ligands as well. However, the difference is that the electrons of the ligands are only attracted to the \(xy\) plane. Any orbital in the xy plane has a higher energy level. There are four different energy levels for the square planar (from the highest energy level to the lowest energy level): dx2-y2, dxy, dz2, and both dxz and dyz.
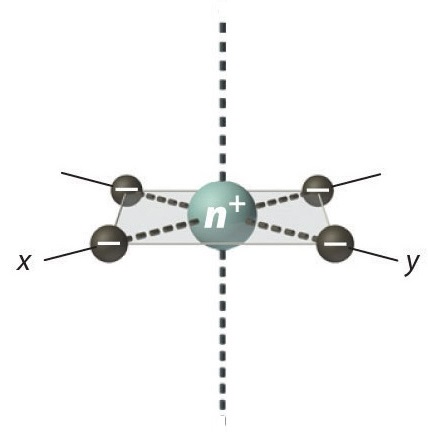
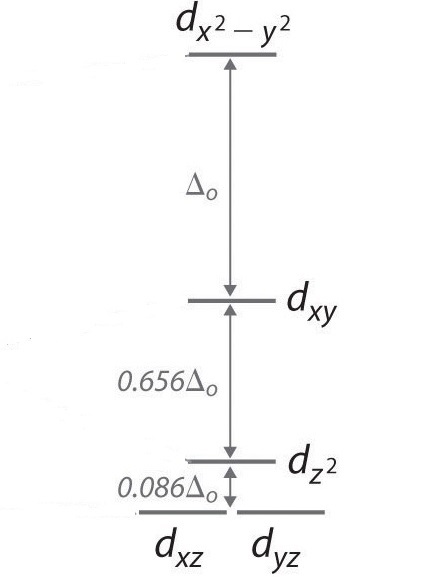
Figure 6: Splitting of the degenerate d-orbitals (without a ligand field) due to an square planar ligand field.
The splitting energy (from highest orbital to lowest orbital) is \(\Delta_{sp}\) and tends to be larger then \(\Delta_{o}\)
\[\Delta_{sp} = 1.74\,\Delta_o \tag{2}\]
Moreover, \(\Delta_{sp}\) is also larger than the pairing energy, so the square planar complexes are usually low spin complexes.
For the complex ion [Fe(Cl)6]3- determine the number of d electrons for Fe, sketch the d-orbital energy levels and the distribution of d electrons among them, list the number of lone electrons, and label whether the complex is paramagnetic or diamagnetic.
Solution
- Step 1: Determine the oxidation state of Fe. Here it is Fe3+. Based on its electron configuration, Fe3+ has 5 d-electrons.
- Step 2: Determine the geometry of the ion. Here it is an octahedral which means the energy splitting should look like:

- Step 3: Determine whether the ligand induces is a strong or weak field spin by looking at the spectrochemical series. Cl- is a weak field ligand (i.e., it induces high spin complexes). Therefore, electrons fill all orbitals before being paired.
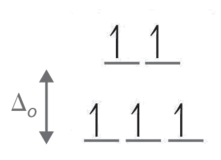
- Step four: Count the number of lone electrons. Here, there are 5 electrons.
- Step five: The five unpaired electrons means this complex ion is paramagnetic (and strongly so).
A tetrahedral complex absorbs at 545 nm. What is the respective octahedral crystal field splitting (\(\Delta_o\))? What is the color of the complex?
Solution
\[\Delta_t = \dfrac{hc}{\lambda}\]
\[\Delta_t = \dfrac{ (6.626 \times 10^{-34} J \cdot s)(3 \times 10^8 m/s)}{545 \times 10^{-9} m}=3.65 \times 10^{-19}\; J \]
However, the tetrahedral splitting (\(\Delta_t\)) is ~4/9 that of the octahedral splitting (\(\Delta_o\)).
\[\Delta_t = 0.44\Delta_o \]
\[\Delta_o = \dfrac{\Delta_t}{0.44} = \dfrac{3.65 \times 10^{-19} J}{0.44} = 8.30 \times 10^{-18}J\]
This is the energy needed to promote one electron in one complex. Often the crystal field splitting is given per mole, which requires this number to be multiplied by Avogadro's Number (\(6.022 \times 10^{23}\)).
This complex appears red, since it absorbs in the complementary green color (determined via the color wheel).

