Spin Pairing Energy
- Page ID
- 661
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Spin pairing energy refers to the energy associated with paired electrons sharing one orbital and its effect on the molecules surrounding it. Electron pairing determining the direction of spin depends on several laws founded by chemists over the years such as Hund's law, the Aufbau principle, and Pauli's exclusion principle. An overview of the different types laws associated with the electron pairing rules.
Introduction
There are two different types of spin paring configurations for an atom or ion: paramagnetic or diamagnetic. Paramagnetic and diamagnetic configurations result from the amount of d electrons in a particular atom. The energy associated with the spin pairing of these configurations relies on a factor of three things, the atom (for its electronic configuration and number of d electrons), the Crystal Field Theory (field splitting of electrons), and the type of ligand field complex (tetrahedral or octahedral). Examples of these three factors affect on spin pairing are shown here;
Being diamagnetic means having all electrons paired and the individual magnetic effects cancel each other out.
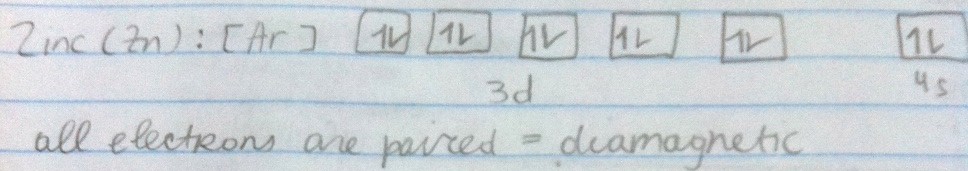
Being paramagnetic means having unpaired electrons and the individual magnetic effects do not cancel each other out. The unpaired electrons carry a magnetic moment that gets stronger with the number of unpaired electrons causing the atom or ion to be attracted to an external magnetic field.

Spin Pairing Energy
According to Hund's Rule, it takes energy to pair electrons, therefore as electrons are added to an orbital, they do it in such a way that they minimize total energy; this causes the 2s orbital to be filled before the 2p orbital. When an electron can singly occupy a given orbital, in a paramagnetic state, that configuration results in high spin energy. However, when two electrons are forced to occupy the same orbital, they experience a interelectronic repulsion effect on each other which in turn increases the total energy of the orbital. The greater this repulsion effect, the greater the energy of the orbital. To calculate this repulsion effect Jorgensen and Slater founded that for any transition metal on the basis of first order perturbation theory can be solved by;
\[E(S) = E(qd^n) + \left [S(S+1)- S(S+1) \right ] D\]
where \(E(qd^n)\) is the weighted mean energy of the configuration, \(S\) is the spin quantum number, \(S(S+1)\) is the average value of the total spin angular momentum and \(D\) is the metal parameter. Therefore,
\[\Delta E = E(S-1)-E(S) = 2SD\]
It is also a general theory that spin pairing energy in the form of repulsion increase from P to D to S orbitals. An example of an element that does not follow this suit is Carbon, whose spin pairing energy increases in the opposite direction (S to D to P). For a clearer picture of how this formula works with the elements in the periodic table, see the attached table. C'dd refers to the repulsion associated with the 3dq occupation only, C', to the intracore repulsion, and C',d to the intershell repulsion between core and d electrons. For comparison, the first column shows D = E/2S, calculated from the frozen orbitals of the configuration average.
Spin Pairing Energy
In general:
- Electron spin pairing energy transition from ↑↑ (in two orbitals) to ↑↓ (in one orbital) is characterized by a decrease of the electronic repulsion.
- Atomic radii for transition metals decrease from left to right because added d electrons do not shield each other very well from the increasing nuclear charge (↑ \(Z_{eff}\)). Atomic radii toward the end of a period increase due to the greater electron-electron repulsion (↑ shielding) as electrons are added to occupied orbitals.
- Very closely associated with crystal field theory (repulsion between electrons of the ligands and the central metal ion) and bonding in complex ions such as octahedral, square-planar, and tetrahedral.
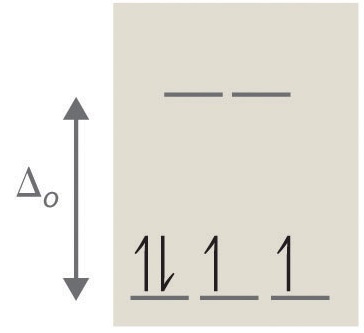
In the example above, the electrons can fill the d-orbitals in two different ways. The electrons can fill lower energy orbitals and pair with an existing electron there resulting in more stability (example on the right). Pairing energy is needed in order to force an electron to fill an orbital that is already occupied with an electron. The electrons can also fill higher energy orbitals and avoid the pairing energy (example on the left). This requires energy and reduces stability.
To figure out whether the electrons pair up or go into higher energy orbital depends on the crystal field splitting energy (\(\Delta\)). If the crystal field splitting energy (Δ) is greater than pairing energy, then greater stability would be obtained if the fourth and fifth electrons get paired with the ones in the lower level. If the crystal field splitting energy (\(\Delta\)) is less than the pairing energy, greater stability is obtained by keeping the electrons unpaired.
In this configuration, it is evident from previous information that the configuration on the left has a higher electronic pair spin than the configuration on the right due to the differing field splitting energy and max number of unpaired electrons. Weak ligands, such as \(H_2\)O and \(F^-\), produce small crystal field splitting resulting in high-spin complexes and strongly paramagnetic. There are only two unpaired electrons in the configuration on the right, which is minimum amount of electrons known as low spin. Strong ligands, such as \(NH_3\) and \(CN^-\), produce large crystal field splitting, leading to low-spin complexes and weakly paramagnetic or sometimes even diamagnetic.
| \(d^n\) | Ion | P, kJ/mol (cm-1) |
|---|---|---|
| \(d^4\) |
\(Cr^{+2}\) \(Mn^{+3}\) |
244.3 (20,425) 301.6 (25,215) |
| \(d^5\) |
\(Mn^{+2}\) \(Fe^{+3}\) |
285.0 (23,825) 357.4 (29,875) |
| \(d^6\) | \(Fe^{+2}\) \(Co^{+3}\) |
229.1 (19,150) 282.6 (23,625) |
| \(d^7\) | \(Co^{+2}\) | 250 (20,800) |
Reference
- Wachters, A. J. H.; Nieuwpoort, W. C. Phys. Rev. B Solid State 1972, 5, 429 1.
- Jorgensen, C. K. “Modern Aspects of Ligand Field Theory”; Elsevier: Amsterdam, New York, 1971.\
- "The Pairing Energy of Co(III) + Co-ordination Chemistry." Chemical Forums (2007). Inorganic Chemistry Forum. Web. 24 May 2010.
- Petrucci, Ralph H. General Chemistry Principles & Modern Applications, Tenth Edition. Upper Saddle River. New Jersey 2011.
- pubs.acs.org/doi/abs/10.1021/ic00136a064
Problems
- What state, paramagnetic or diamagnetic has a higher spin pairing repulsion?
- What is the electron configuration of Mn?
- What is the spin pairing configuration of Mn?
- How does the spin pairing configuration of Mn affect the spin energy?
- What is the electron spin energy differ between these two complexes:
A) [Fe(NO2)6]3−
B) [FeBr6]3−
Answers
- Paramagnetic
- [Ar] 3d3
- Paramagnetic
- Because Mn has a paramagnetic configuration, its spin energy is high
- A) NO has a high crystal field splitting energy therefore causing the electrons to be forced together in lower state energy orbitals making most of them diamagnetic. This configuration causes this complex to have low spin energy.
B) Br has a very small crystal field splitting energy, causing the electrons to disperse among the orbitals freely. This allows a paramagnetic state, causing this complex to have high spin energy.

