13.3: Molecular orbitals for three-carbon systems
- Page ID
- 225856
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Propene and higher alkenes
The pi-molecular orbitals in propene (CH3-CH=CH2) are essentially the same as those found in ethene, and so we need not examine them further.
Allene
However, when we look at allene (propa-1,2-diene), where we have two double bonds shared between three carbons, we find a new situation. The two outer carbons are still sp2 hybridized, but the central carbon is now sp-hybridized with two double bonds coming from it. This central carbon thus provides two p-orbitals – one for each pi bond – and these two different p-orbitals have to be perpendicular, leading to a twisted structure as shown:
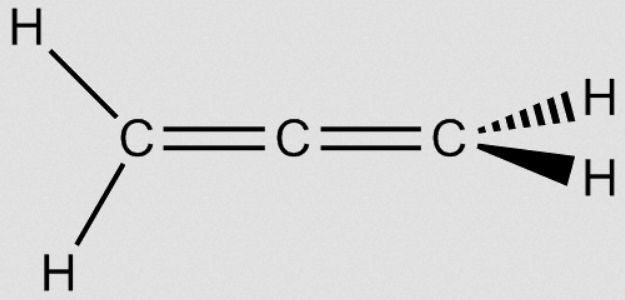 | 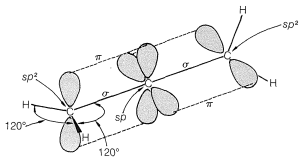 |
Since these pi-orbitals are perpendicular, they are independent of one another; however, if both pi-bonding are filled with electrons then there will be some repulsion between them, causing slight destabilization. So for structures like this with neighboring double bonds, there is no stabilizing effect, and in fact allene-type systems are not particularly common in nature but for one major exception – carbon dioxide.
For more information on the structure of allene, see Zimmerman, H. Journal of Chemical Education, 1977, 54, 609.
Conjugated dienes are more stable than non conjugated dienes (both isolated and cumulated) due to factors such as delocalization of charge through resonance and hybridization energy. This can also explain why allylic radicals are much more stable than secondary or even tertiary carbocations. This is all due to the positioning of the pi orbitals and ability for overlap to occur to strengthen the single bond between the two double bonds.
Allylic systems
Conjugation occurs when p orbitals on three or more adjacent sp2 (or occasionally sp) hybridized atoms can overlap Conjugation tends to stabilize molecules. Allylic (also called 2-propenyl) carbocations are a common conjugated system.
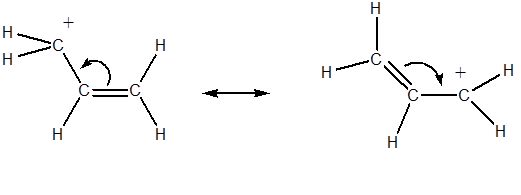
The positive charge of a carbocation is contained in an empty p orbital of a sp2 hybridized carbon. This allows for overlap with double bonds. The positive charge is more stable because it is spread over 2 carbons.
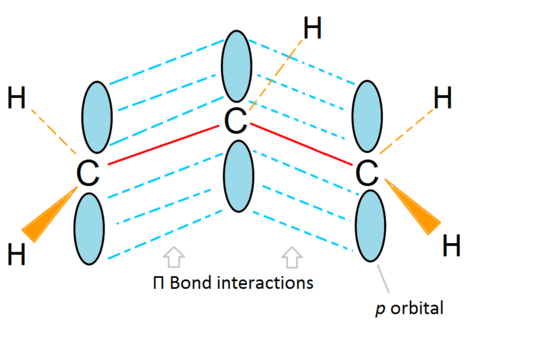
Molecular orbitals of an allyl carbocation
The stability of the allyl carbocation is due to a conjugated π electron system. A “double bond” doesn’t really exist. Instead, it is a group of 3 adjacent, overlapping, non-hybridized p orbitals we call a conjugated π electron system. You can clearly see the interactions between all three of the p orbitals from the three carbons resulting in a really stable cation. It all comes down to where the location of the electron-deficient carbon is.
Molecular orbital descriptions can explain the stability of the allyl system:
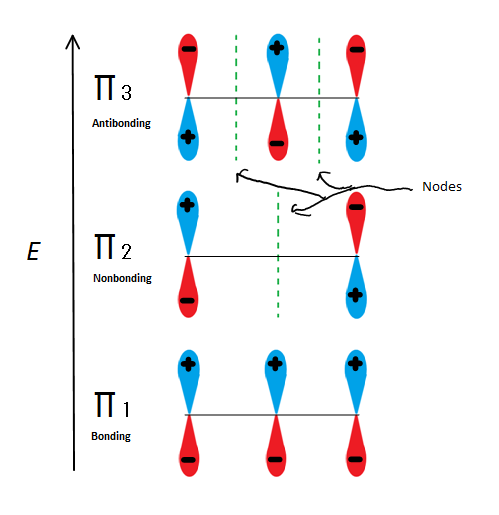
If we just take the π molecular orbital and not any of the s, we get three of them. π1 is bonding with no nodes, π2 is nonbonding (In other words, the same energy as a regular p-orbital) with a node, and π3 is antibonding with 2 nodes (none of the orbitals are interacting). The first two electrons will go into the π1 molecular orbital, regardless of whether it is a cation, radical, or anion. If it is a radical or anion, the next electron goes into the π2 molecular orbital. The last anion electron goes into the nonbonding orbital also. So no matter what kind of carbon center exists, no electron will ever go into the antibonding orbital.
The bonding orbitals are the lowest energy orbitals and are favorable, which is why they are filled first (the aufbau principle). Even though the nonbonding orbitals can be filled, the overall energy of the system is still lower and more stable due to the filled bonding molecular orbitals.
This figure also shows that π2 is the only molecular orbital where the number of electrons varies, and it is also where a single node passes through the middle. Because of this, the charges of the molecule are mainly on the two terminal carbons and not the middle carbon.
This molecular orbital description can also illustrate the stability of allylic carbon centers in figure 7.
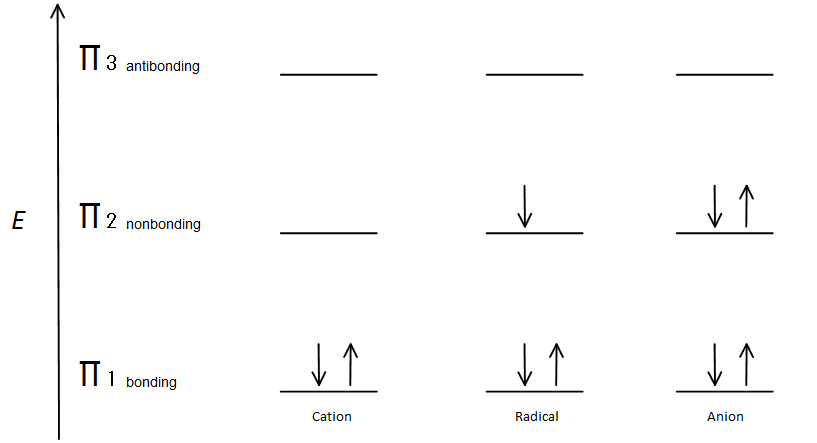
The π bonding orbital is lower in energy than the nonbonding p orbital. Since every carbon center shown has two electrons in the lower energy, bonding π orbitals, the energy of each system is lowered overall (and thus more stable), regardless of cation, radical, or anion.
- Additional text on allene and allylic systems. Authored by: Martin A. Walker. Provided by: SUNY Potsdam. License: CC BY-SA: Attribution-ShareAlike
- 14.1: Stability of Conjugated Dienes - Molecular Orbital Theory . Authored by: Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University); Prof. Steven Farmer (Sonoma State University); William Reusch, Professor Emeritus (Michigan State U.); Tim Soderberg (University of Minnesota, Morris). Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Map%3A_Organic_Chemistry_(McMurry)/Chapter_14%3A_Conjugated_Compounds_and_Ultraviolet_Spectroscopy/14.01_Stability_of_Conjugated_Dienes%3A__Molecular_Orbital_Theory. Project: Chemistry LibreTexts. License: CC BY-NC: Attribution-NonCommercial
- 3D structure of allene. Authored by: marcosm21. Provided by: Wikimedia Commons. Located at: https://commons.wikimedia.org/wiki/File:Aleno.png. License: CC BY-SA: Attribution-ShareAlike
- 13.5: Cumulated Alkadienes. Authored by: John D. Robert and Marjorie C. Caserio. Located at: https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Book%3A_Basic_Principles_of_Organic_Chemistry_(Roberts_and_Caserio)/13%3A_Polyfunctional_Compounds%2C_Alkadienes%2C_and_Approaches_to_Organic_Synthesis/13.05%3A_Cumulated_Alkadienes. Project: Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. . License: CC BY-NC: Attribution-NonCommercial

