13.5: Cumulated Alkadienes

Structure and Stereoisomerism

The 1,2-dienes, which have cumulated double bonds, commonly are called allenes. The simplest example is 1,2-propadiene,

Figure 13-4). In this formulation each of two electrons of the central atom form collinear \(sp \: \sigma\) bonds to the terminal \(sp^2\)-hybridized carbons. The two remaining electrons of the central carbon occupy \(p\) orbitals and form \(\pi\) bonds through overlap of these \(p\) orbitals and the \(p\) orbitals of the terminal carbons.

Figure 13-3: Ball-and-stick model of 1,2-propadiene.

Figure 13-4: Atomic-orbital model of 1,2-propadiene.

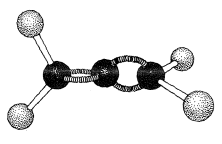
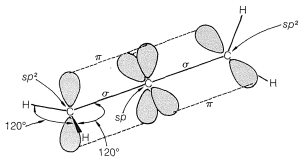
Allenes of the type \(\ce{RR'C=C=CRR'}\) are chiral molecules and can exist in two stereoisomeric forms, one being the mirror image of the other and neither being superimposable on the other (i.e., enantiomers, Figure 13-5).

Figure 13-5: Enantiomers of a substituted allene of the type \(\ce{RR'C=C=CRR'}\).

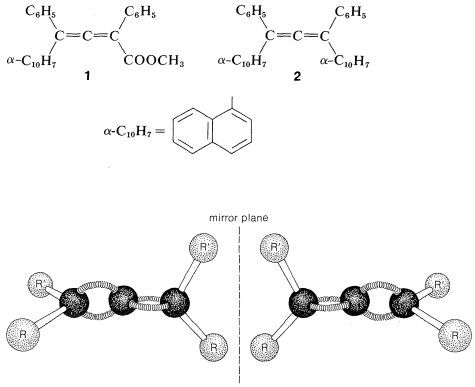
Verification of the chirality of such allenes (originally proposed by van’t Hoff in 1875) was slow in coming and was preceded by many unsuccessful attempts to resolve suitably substituted allenes into their enantiomers. The first successful resolutions were achieved in 1935 for the enantiomers of two compounds \(1\) and \(2\). This was a classic achievement because it dispelled the suspicion prevalent at the time that rotation about the bonds of the cumulated diene system was free enough to preclude the isolation of configurationally stable enantiomers.

The chirality observed in this kind of substituted allene is a consequence of dissymmetry resulting from restricted rotation about the double bonds, not because of a tetrahedral atom carrying four different groups. Restricted rotation occurs in many other kinds of compounds and a few examples are shown in Table 13-3, which includes trans-cycloalkenes (Section 12-7), cycloalkylidenes, spiranes, and ortho-substituted biphenyl compounds. To have enantiomers, the structure must not have a plane or center of symmetry (Section 5-5).

Table 13-3: Examples of Chiral Substances Resulting from Restricted Rotation About Double or Single Bonds\(^a\)

The chirality of biphenyls results from restricted rotation about a single bond imposed by the bulky nature of ortho substituents. Models will help you visualize the degree of difficulty of having the substituents pass by one another. If \(\ce{X} = \ce{H}\) and \(\ce{Y} = \ce{F}\) (Table 13-3), the enantiomers are not stable at room temperature; if \(\ce{X} = \ce{H}\) and \(\ce{Y} = \ce{Br}\), they are marginally stable; if \(\ce{X} = \ce{H}\) and \(\ce{Y} = \ce{I}\), the rate of loss of optical activity is about 700 times slower than with \(\ce{Y} = \ce{Br}\). This is in keeping with the fact that the atomic size of the halogens increases in the order \(\ce{F} < \ce{Br} < \ce{I}\).

Cis-Trans Isomerism

In a cumulated triene, or any cumulated polyene with an odd number of double bonds, the atoms connected to the terminal carbons lie in the same plane, just as they do in an ordinary alkene. Van’t Hoff pointed out that suitably substituted cumulated polyenes of this type should then have cis and trans forms:

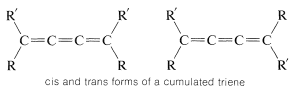
Like the resolution of allenes, the separate existence of cis and trans isomers of cumulated trienes was not verified until many years after van’t Hoff’s original predictions, but a separation finally was achieved, in 1954, by R. Kuhn and K. Scholler for compounds \(3\) and \(4\):

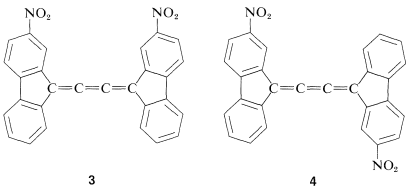
There are relatively few cis-trans forms of 1,2,3-alkatrienes known. They appear to interconvert readily on mild heating, which suggests that one of the double bonds has a lower rotational barrier than is normal for an alkene double bond.

Chemistry of Allenes

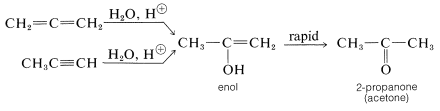
The properties of allenes are similar to those of alkenes, although the pure compounds often are difficult to prepare and are not indefinitely stable. Allenes undergo many of the usual double-bond reactions, being readily hydrogenated, adding bromine, and being oxidized with potassium permanganate solution. The hydration of allenes resembles the hydration of alkynes in giving initially an unstable enol that rapidly rearranges to a ketone:

Allenes are not as stable as dienes with conjugated or isolated double bonds. The heats of hydrogenation (Table 11-2) indicate that the order of stability is conjugated dienes \(>\) isolated dienes \(>\) cumulated dienes. The relative instability of allenes probably reflects extra strain as the result of one carbon atom forming two double bonds. 1,2-Propadiene is slightly more strained than that of propyne. It is not surprising then that 1,2-propadiene isomerizes to propyne. This isomerization occurs under the influence of strongly basic substances such as sodium amide in liquid ammonia or potassium hydroxide in ethyl alcohol:

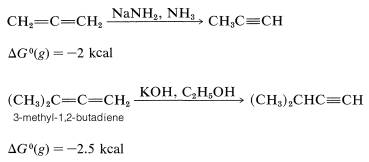
Indeed, one of the difficulties associated with syntheses of allenes and alkynes (which often are carried out in the presence of strong bases) is the concurrent formation of isomerization products.

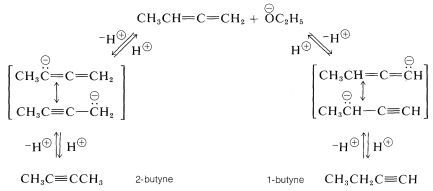
The basic catalyst in the isomerization of 1,2-butadiene to butynes acts by removing an alkenic proton from the hydrocarbon. Two different anions can be formed, each of which is stabilized by electron delocalization involving the adjacent multiple bond. Either anion can react with the solvent by proton transfer to form the starting material or an alkyne. At equilibrium the most stable product, which is 2-butyne, predominates [1-butyne \(\left( g \right) \rightleftharpoons\) 2-butyne \(\left( g \right)\), \(\Delta G^0 = -4.0 \: \text{kcal mol}^{-1}\)]:

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."