5.7: Problems
- Page ID
- 219817
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Suppose you use a serial dilution to prepare 100 mL each of a series of standards with concentrations of \(1.00 \times10^{-5}\), \(1.00 \times10^{-4}\), \(1.00 \times10^{-3}\), and \(1.00 \times10^{-2}\) M from a 0.100 M stock solution. Calculate the uncertainty for each solution using a propagation of uncertainty, and compare to the uncertainty if you prepare each solution as a single dilution of the stock solution. You will find tolerances for different types of volumetric glassware and digital pipets in Table 4.2.1 and Table 4.2.2. Assume that the uncertainty in the stock solution’s molarity is ±0.0002.
2. Three replicate determinations of Stotal for a standard solution that is 10.0 ppm in analyte give values of 0.163, 0.157, and 0.161 (arbitrary units). The signal for the reagent blank is 0.002. Calculate the concentration of analyte in a sample with a signal of 0.118.
3. A 10.00-g sample that contains an analyte is transferred to a 250-mL volumetric flask and diluted to volume. When a 10.00 mL aliquot of the resulting solution is diluted to 25.00 mL it gives a signal of 0.235 (arbitrary units). A second 10.00-mL portion of the solution is spiked with 10.00 mL of a 1.00-ppm standard solution of the analyte and diluted to 25.00 mL. The signal for the spiked sample is 0.502. Calculate the weight percent of analyte in the original sample.
4. A 50.00 mL sample that contains an analyte gives a signal of 11.5 (arbitrary units). A second 50 mL aliquot of the sample, which is spiked with 1.00 mL of a 10.0-ppm standard solution of the analyte, gives a signal of 23.1. What is the analyte’s concentration in the original sample?
5. A standard additions calibration curve based on Equation 5.3.10 places \(S_{spike} \times (V_o + V_{std})\) on the y-axis and \(C_{std} \times V_{std}\) on the x-axis. Derive equations for the slope and the y-intercept and explain how you can determine the amount of analyte in a sample from the calibration curve. In addition, clearly explain why you cannot plot Sspike on the y-axis and \(C_{std} \times \{V_{std}/(V_o + V_{std})\}\) on the x-axis.
6. A standard sample contains 10.0 mg/L of analyte and 15.0 mg/L of internal standard. Analysis of the sample gives signals for the analyte and the internal standard of 0.155 and 0.233 (arbitrary units), respectively. Sufficient internal standard is added to a sample to make its concentration 15.0 mg/L. Analysis of the sample yields signals for the analyte and the internal standard of 0.274 and 0.198, respectively. Report the analyte’s concentration in the sample.
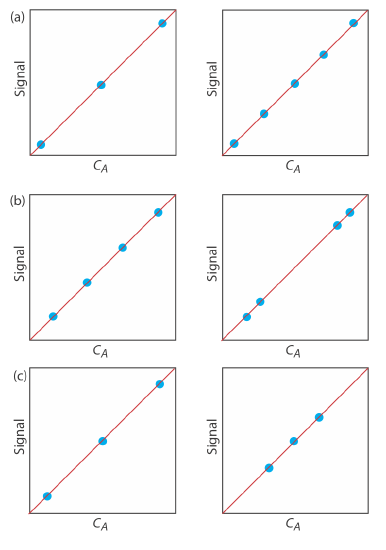
7. For each of the pair of calibration curves shown ibelow, select the calibration curve that uses the more appropriate set of standards. Briefly explain the reasons for your selections. The scales for the x-axis and the y-axis are the same for each pair.
8. The following data are for a series of external standards of Cd2+ buffered to a pH of 4.6.
| [Cd2+] (nM) | 15.4 | 30.4 | 44.9 | 59.0 | 72.7 | 86.0 |
| \(S_{meas}\) (nA) | 4.8 | 11.4 | 18.2 | 26.6 | 32.3 | 37.7 |
(a) Use a linear regression analysis to determine the equation for the calibration curve and report confidence intervals for the slope and the y-intercept.
(b) Construct a plot of the residuals and comment on their significance.
At a pH of 3.7 the following data were recorded for the same set of external standards.
| [Cd2+] (nM) | 15.4 | 30.4 | 44.9 | 59.0 | 72.7 | 86.0 |
| \(S_{meas}\) (nA) | 15.0 | 42.7 | 58.5 | 77.0 | 101 | 118 |
(c) How much more or less sensitive is this method at the lower pH?
(d) A single sample is buffered to a pH of 3.7 and analyzed for cadmium, yielding a signal of 66.3 nA. Report the concentration of Cd2+ in the sample and its 95% confidence interval.
The data in this problem are from Wojciechowski, M.; Balcerzak, J. Anal. Chim. Acta 1991, 249, 433–445.
9. To determine the concentration of analyte in a sample, a standard addition is performed. A 5.00-mL portion of sample is analyzed and then successive 0.10-mL spikes of a 600.0 ppb standard of the analyte are added, analyzing after each spike. All samples were diluted to 10.00 mL before measuring the signal. The following table shows the results of this analysis.
| \(V_{spike}\) (mL) | 0.00 | 0.10 | 0.20 | 0.30 |
| \(S_{total}\) (arbitrary units) | 0.119 | 0.231 | 0.339 | 0.442 |
Construct an appropriate standard additions calibration curve and use a linear regression analysis to determine the concentration of analyte in the original sample and its 95% confidence interval.
10. Troost and Olavsesn investigated the application of an internal standardization to the quantitative analysis of polynuclear aromatic hydrocarbons. The following results were obtained for the analysis of phenanthrene using isotopically labeled phenanthrene as an internal standard. Each solution was analyzed twice.
|
\(C_A/C_{IS}\) |
0.50 | 1.25 | 2.00 | 3.00 | 4.00 |
| \(S_A/S_{IS}\) |
0.514 0.522 |
0.993 1.024 |
1.486 1.471 |
2.044 2.080 |
2.342 2.550 |
(a) Determine the equation for the calibration curve using a linear regression, and report confidence intervals for the slope and the y-intercept. Average the replicate signals for each standard before you complete the linear regression analysis.
(b) Based on your results explain why the authors concluded that the internal standardization was inappropriate.
The data in this problem are from Troost, J. R.; Olavesen, E. Y. Anal. Chem. 1996, 68, 708–711.
11. In Chapter 4.6. we used a paired t-test to compare two analytical methods that were used to analyze independently a series of samples of variable composition. An alternative approach is to plot the results for one method versus the results for the other method. If the two methods yield identical results, then the plot should have an expected slope, \(\beta_1\), of 1.00 and an expected y-intercept, \(\beta_0\), of 0.0. We can use a t-test to compare the slope and the y-intercept from a linear regression to the expected values. The appropriate test statistic for the y-intercept is found by rearranging Equation 5.4.10.
\[t_{exp} = \frac {|\beta_0 - b_0|} {s_{b_0}} = \frac {|b_0|} {s_{b_0}} \nonumber\]
Rearranging Equation 5.4.9 gives the test statistic for the slope.
\[t_{exp} = \frac {|\beta_1 - b_1} {s_{b_1}} = \frac {|b_1|} {s_{b_1}} \nonumber\]
Reevaluate the data in Problem 25 from Chapter 4 using the same significance level as in the original problem.
Although this is a common approach for comparing two analytical methods, it does violate one of the requirements for an unweighted linear regression—that indeterminate errors affect y only. Because indeterminate errors affect both analytical methods, the result of an unweighted linear regression is biased. More specifically, the regression underestimates the slope, b1, and overestimates the y-intercept, b0. We can minimize the effect of this bias by placing the more precise analytical method on the x-axis, by using more samples to increase the degrees of freedom, and by using samples that uniformly cover the range of concentrations.
For more information, see Miller, J. C.; Miller, J. N. Statistics for Analytical Chemistry, 3rd ed. Ellis Horwood PTR Prentice-Hall: New York, 1993. Alternative approaches are found in Hartman, C.; Smeyers-Verbeke, J.; Penninckx, W.; Massart, D. L. Anal. Chim. Acta 1997, 338, 19–40, and Zwanziger, H. W.; Sârbu, C. Anal. Chem. 1998, 70, 1277–1280.
12. Consider the following three data sets, each of which gives values of y for the same values of x.
| x | y1 | y2 | y3 |
| 10.00 | 8.04 | 9.14 | 7.46 |
| 8.00 | 6.95 | 8.14 | 6.77 |
| 13.00 | 7.58 | 8.74 | 12.74 |
| 9.00 | 8.81 | 8.77 | 7.11 |
| 11.00 | 8.33 | 9.26 | 7.81 |
| 14.00 | 9.96 | 8.10 | 8.84 |
| 6.00 | 7.24 | 6.13 | 6.08 |
| 4.00 | 4.26 | 3.10 | 5.39 |
| 12.00 | 10.84 | 9.13 | 8.15 |
| 7.00 | 4.82 | 7.26 | 6.42 |
| 5.00 | 5.68 | 4.74 | 5.73 |
(a) An unweighted linear regression analysis for the three data sets gives nearly identical results. To three significant figures, each data set has a slope of 0.500 and a y-intercept of 3.00. The standard deviations in the slope and the y-intercept are 0.118 and 1.125 for each data set. All three standard deviations about the regression are 1.24. Based on these results for a linear regression analysis, comment on the similarity of the data sets.
(b) Complete a linear regression analysis for each data set and verify that the results from part (a) are correct. Construct a residual plot for each data set. Do these plots change your conclusion from part (a)? Explain.
(c) Plot each data set along with the regression line and comment on your results.
(d) Data set 3 appears to contain an outlier. Remove the apparent outlier and reanalyze the data using a linear regression. Comment on your result.
(e) Briefly comment on the importance of visually examining your data.
These three data sets are taken from Anscombe, F. J. “Graphs in Statistical Analysis,” Amer. Statis. 1973, 27, 17-21.
13. Fanke and co-workers evaluated a standard additions method for a voltammetric determination of Tl. A summary of their results is tabulated in the following table.
| ppm Tl added | Instrument Response (\(\mu\)A) | ||||||
| 0.000 | 2.53 | 2.50 | 2.70 | 2.63 | 2.70 | 2.80 | 2.52 |
| 0.387 | 8.42 | 7.96 | 8.54 | 8.18 | 7.70 | 8.34 | 7.98 |
| 1.851 | 29.65 | 28.70 | 29.05 | 28.30 | 29.20 | 29.95 | 28.95 |
| 5.734 | 84.8 | 85.6 | 86.0 | 85.2 | 84.2 | 86.4 | 87.8 |
Use a weighted linear regression to determine the standardization relationship for this data.
The data in this problem are from Franke, J. P.; de Zeeuw, R. A.; Hakkert, R. Anal. Chem. 1978, 50, 1374–1380.


