5.10: Lattice Energy - The Born-Haber cycle

Ionic solids tend to be very stable compounds. The enthalpies of formation of the ionic molecules cannot alone account for this stability. These compounds have an additional stability due to the lattice energy of the solid structure. However, lattice energy cannot be directly measured. The Born-Haber cycle allows us to understand and determine the lattice energies of ionic solids. Lattice Energy is used to explain the stability of ionic solids. Some might expect such an ordered structure to be less stable because the entropy of the system would be low. However, the crystalline structure allows each ion to interact with multiple oppositely charge ions, which causes a highly favorable change in the enthalpy of the system. A lot of energy is released as the oppositely charged ions interact. It is this that causes ionic solids to have such high melting and boiling points. Some require such high temperatures that they decompose before they can reach a melting and/or boiling point.

Lattice Energy

Lattice Energy is a type of potential energy. Although there are two commonly used ways of defining lattice enthalpy which directly contradict each other, and we will primarily use the first of these:

• The lattice energy is the energy required to break apart an ionic solid and convert its component atoms into gaseous ions. This definition causes the value for the lattice energy to always be positive, since this will always be an endothermic reaction. In other words, you are looking at a downward arrow on Figure \(\PageIndex{1}\).

\[\ce{M_{a} L_{b} (s) \rightarrow a M^{b+} (g) + b X^{a-} (g) } \nonumber \]

• The lattice energy is the energy released when gaseous ions bind to form an ionic solid. As implied in the definition, this process will always be exothermic, and thus the value for lattice energy will be negative. Its values are usually expressed with the units kJ/mol. In other words, you are looking at an upward arrow on Figure \(\PageIndex{1}).

\[\ce{ a M^{b+} (g) + b X^{a-} (g) \rightarrow M_{a}L_{b}(s) } \nonumber \]

Figure \(\PageIndex{1}\): Enthalpy diagram for NaCl(s); for sodium chloride, the solid is more stable than the gaseous ions by 787 kJ mol^-1. (CC-BY-NC-SA; Jim Clark)

Definitions

You may prefer to refer to the lattice enthalpy associated with dissociation or formation of the lattice

• The lattice dissociation enthalpy is the enthalpy change needed to convert 1 mole of solid crystal into its scattered gaseous ions. Lattice dissociation enthalpies are always positive.
• The lattice formation enthalpy is the enthalpy change when 1 mole of solid crystal is formed from its separated gaseous ions. Lattice formation enthalpies are always negative.

Values of lattice energies for various solids have been given in the literature, especially for some common solids. A few are provided in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Lattice Energies (kJ/mol) of Some Salts

Solid	U	Solid	U	Solid	U	Solid	U
LiF	1036	LiCl	853	LiBr	807	LiI	757
NaF	923	NaCl	786	NaBr	747	NaI	704
KF	821	KCl	715	KBr	682	KI	649
MgF2	2957	MgCl2	2526	MgBr2	2440	MgI2	2327

Factors Affecting Lattice Enthalpy

The following trends are obvious at a glance of the data in Table \(\PageIndex{1}\):

• As the ionic radii of either the cation or anion increase, the lattice energies decrease.
• The solids consists of divalent ions have much larger lattice energies than solids with monovalent ions.

Lattice enthalpy is a measure of the strength of the forces between the ions in an ionic solid. Those forces are only completely broken when the ions are present as gaseous ions, scattered so far apart that there is negligible attraction between them. The greater the lattice enthalpy, the stronger the forces.The force of attraction between oppositely charged particles is described by Coulomb's law

The charges on the ions

Sodium chloride and magnesium oxide have exactly the same arrangements of ions in the crystal lattice, but the lattice enthalpies are very different. You can see that the lattice enthalpy of magnesium oxide is much greater than that of sodium chloride. That's because in magnesium oxide, 2+ ions are attracting 2- ions; in sodium chloride, the attraction is only between 1+ and 1- ions.

Figure \(\PageIndex{2}\): A comparison of the lattice enthalpies of NaCl and MgO. (CC-BY-NC-SA; Jim Clark)

The Radius of the Ions

The lattice enthalpy of magnesium oxide is also increased relative to sodium chloride because magnesium ions are smaller than sodium ions, and oxide ions are smaller than chloride ions. That means that the ions are closer together in the lattice, and that increases the strength of the attractions.

This effect of ion size on lattice enthalpy is clearly observed as you go down a Group in the Periodic Table. For example, as you go down Group 7 of the Periodic Table from fluorine to iodine, you would expect the lattice enthalpies of their sodium salts to fall as the negative ions get bigger - and that is the case:

Figure \(\PageIndex{3}\): Lattice enthalpies of sodium halides. (CC-BY-NC-SA; Jim Clark)

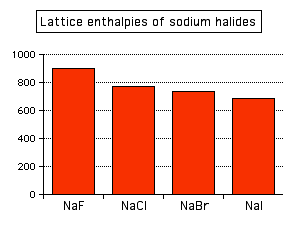
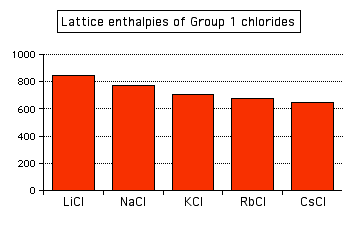
Attractions are governed by the distances between the centers of the oppositely charged ions, and that distance is obviously greater as the negative ion gets bigger. And you can see exactly the same effect if as you go down Group 1. The next bar chart shows the lattice enthalpies of the Group 1 chlorides.

Figure \(\PageIndex{4}\): Lattice enthalpies of Group 1 chlorides. (CC-BY-NC-SA; Jim Clark)

The Born-Haber Cycle

The Born-Haber cycle is used to estimate the lattice energy of an ionic solid. The Born-Haber Cycle uses several familiar concepts to determine the lattice energy of an ionic solid: ionization energy, electron affinity, dissociation energy, sublimation energy, heat of formation, and Hess's Law.

• Ionization Energy is the energy required to remove an electron from a neutral atom or an ion. This process always requires an input of energy, and thus will always have a positive value. In general, ionization energy increases across the periodic table from left to right, and decreases from top to bottom. There are some excepts, usually due to the stability of half-filled and completely filled orbitals.
• Electron Affinity is the energy released when an electron is added to a neutral atom or an ion. Usually, energy released would have a negative value, but due to the definition of electron affinity, it is written as a positive value in most tables. Therefore, when used in calculating the lattice energy, we must remember to subtract the electron affinity, not add it. In general, electron affinity increases from left to right across the periodic table and decreases from top to bottom.
• Dissociation energy is the energy required to break apart a compound. The dissociation of a compound is always an endothermic process, meaning it will always require an input of energy. Therefore, the change in energy is always positive. The magnitude of the dissociation energy depends on the electronegativity of the atoms involved.
• Atomization energy is the energy required to cause a change of phase from solid to gas, bypassing the liquid phase. This is an input of energy, and thus has a positive value. It may also be referred to as the sublimation energy.
• The heat of formation is the change in energy when forming a compound from its elements. This may be positive or negative, depending on the atoms involved and how they interact.
• Hess's Law states that the overall change in energy of a process can be determined by breaking the process down into steps, then adding the changes in energy of each step. The Born-Haber Cycle is essentially Hess's Law applied to an ionic solid.

Enthalpy of Atomization

The standard atomization enthalpy, \(\Delta H^o_a\), is the enthalpy change when 1 mole of gaseous atoms is formed from the element in its standard state. Enthalpy change of atomization is always positive. You are always going to have to supply energy to break an element into its separate gaseous atoms. All of the following equations represent changes involving atomization enthalpy:

\[ \dfrac{1}{2} Cl_2 (g) \rightarrow Cl(g) \;\;\;\; \Delta H^o_a=+122\, kJ\,mol^{-1} \nonumber \]

\[ \dfrac{1}{2} Br_2 (l) \rightarrow Br(g) \;\;\;\; \Delta H^o_a=+122\, kJ\,mol^{-1} \nonumber \]

\[ Na (s) \rightarrow Na(g) \;\;\;\; \Delta H^o_a=+107\, kJ\,mol^{-1} \nonumber \]

Notice particularly that the "mol^-1" is per mole of atoms formed - NOT per mole of element that you start with. You will quite commonly have to write fractions into the left-hand side of the equation. Getting this wrong is a common mistake.

How to Use the Born-Haber Cycle

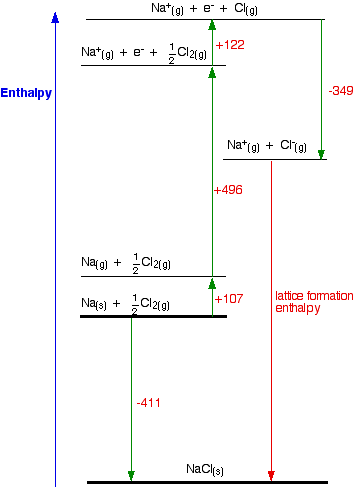
Consider the Born-Haber cycle for sodium chloride (Figure \(\PageIndex{5}\)).The values used in the Born-Haber Cycle are all predetermined changes in enthalpy for the processes described above. Hess' Law allows us to add or subtract these values, which allows us to determine the lattice energy.

Figure \(\PageIndex{5}\): Born-Haber Cycle for NaCl. (CC-BY-NC-SA; Jim Clark)

Step 0

Start with the balanced chemical equation for the formation of NaCl(s) from its elements in their standard states:

\[\ce_Na(s) + \frac{1}{2} Cl_2(g) \rightarrow NaCl(s), \Delta H_{formation} =-411 kJ/mol \nonumber\]

Elements in their standard states have an enthalpy of zero, and energy is released when a compound is formed from its elements in their standard states. This is the energy of formation, and will be used at the end of the process to determine the lattice energy. The energy of formation is not directly determined, thus the a series of reactions will be used to convert the elements in their standard states into non-standard states and then eventually into the compound. The sum of the energy changes in these steps will be equal to the heat of formation of the compound.

Step 1

The Born-Haber Cycle requires that the elements involved in the reaction are in their gaseous forms.

\[\ce_Na(s) \rightarrow Na(g), \Delta H_{atom,\,Na}=107 kJ/mol \nonumber\]

Step 2

Although Cl₂ exists as a gas in its standard state, however, it also exists as a polyatomic species. The energy associated with changing Cl₂ into 2Cl must also be considered.

\[\ce \frac{1}{2} Cl_2(g) \rightarrow Cl(g), \Delta H_{atom,\,Cl}=122 kJ/mol \nonumber\]

Step 3

The gaseous atoms need to be changed into their ionic forms, as they would exist in the ionic solid. The Na(g) must be ionized to its cation form.

\[\ce_Na(g) \rightarrow Na^+(g) + e^-, \Delta H_{IE_1,\,Na}=496 kJ/mol \nonumber\]

Step 4

The chlorine must lose an electron to form its anion.

\[\ce_Cl(g) + e^- \rightarrow Cl^- (g), \Delta H_{EA_1 \,Cl}=-349 kJ/mol \nonumber\]

Step 5

Now the cation and anion will be combined to form the ionic solid. This will cause a release of energy, which is called the lattice energy. 

\[\ce_Na^+(g) + Cl^- (g) \rightarrow NaCl(s), \Delta H_{lattice} \nonumber\]

Step 6

Steps the energy changes for steps 0 through 5 can be combined into one equation:

\[\ce_\Delta H_{formation} =\Delta H_{atom,\,Na}+\Delta H_{atom,\,Cl}+\Delta H_{IE_1,\,Na}+\Delta H_{EA_1 \,Cl}+\Delta H_{lattice} \nonumber\]

\[\ce_-411 \frac{kJ}{mol} = 107 \frac{kJ}{mol} +122 \frac{kJ}{mol} + 496 \frac{kJ}{mol} +(-340 \frac{kJ}{mol}) +\Delta H_{lattice} \nonumber\]

Rearrangement to solve for lattice energy gives the equation:

\[\ce_\Delta H_{lattice}=\Delta H_{formation} -(\Delta H_{atom,\,Na}+\Delta H_{atom,\,Cl}+\Delta H_{IE_1,\,Na}+\Delta H_{EA_1 \,Cl}) \nonumber\]

\[\ce_\Delta H_{lattice}= -411 \frac{kJ}{mol} - (107 \frac{kJ}{mol} +122 \frac{kJ}{mol} + 496 \frac{kJ}{mol} +(-340 \frac{kJ}{mol})) \nonumber\]

\[\ce_\Delta H_{lattice}=-411 \frac{kJ}{mol} - 107 \frac{kJ}{mol} -122 \frac{kJ}{mol} - 496 \frac{kJ}{mol} +340 \frac{kJ}{mol} \nonumber\]

\[\ce_\Delta H_{lattice}=-787

Example \(\PageIndex{1}\): Born-Haber Cycle for MgCl₂

Why is magnesium chloride MgCl₂ rather than MgCl or MgCl₃ (or any other formula you might like to choose)?

It turns out that MgCl₂ is the formula of the compound which has the most negative enthalpy of formation - in other words, it is the most stable one relative to the elements magnesium and chlorine. Let's look at this in terms of Born-Haber cycles of the imaginary compounds MgCl and MgCl₃.

This will require us to use theoretical values for their lattice enthalpies. We cannot use experimental ones, because these compounds do not exist! The exact values do not matter too much anyway, because the results are so dramatically clear-cut.

Solution

Born-Haber cycle for MgCl

\[ \ce{Mg(s) + 1/2 Cl_2(g) \rightarrow MgCl (s)} \nonumber \]

 

ΔH_f = +148 + 738 + 122 - 349 - 753

ΔH_f = -94 kJ mol^-1

The compound MgCl is definitely energetically more stable than its elements. This cycle is drawn very roughly to scale, but that is going to become more and more difficult as we look at the other two possible formulae. You can see from the diagram that the enthalpy change of formation can be found just by adding up all the other numbers in the cycle, and we can do this just as well in a table:

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
atomization enthalpy of Cl	+122
electron affinity of Cl	-349
lattice enthalpy	-753
calculated ΔHf	-94

1. The Born-Haber cycle for MgCl₂

The equation for the enthalpy change of formation this time is

\[ \ce{Mg (s) + Cl2 (g) \rightarrow MgCl2 (s)} \nonumber \]

So how does that change the numbers in the Born-Haber cycle?

• You need to add in the second ionization energy of magnesium, because you are making a 2+ ion.
• You need to multiply the atomization enthalpy of chlorine by 2, because you need 2 moles of gaseous chlorine atoms.
• You need to multiply the electron affinity of chlorine by 2, because you are making 2 moles of chloride ions.
• You obviously need a different value for lattice enthalpy.

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
2nd IE of Mg	+1451
atomization enthalpy of Cl (x 2)	+244
electron affinity of Cl (x 2)	-698
lattice enthalpy	-2526
calculated ΔHf	-643

You can see that much more energy is released when you make MgCl₂ than when you make MgCl. Why is that? You need to put in more energy to ionize the magnesium to give a 2+ ion, but a lot more energy is released as lattice enthalpy. That is because there are stronger ionic attractions between 1- ions and 2+ ions than between the 1- and 1+ ions in MgCl. So what about MgCl₃? The lattice energy here would be even greater.

3. The Born-Haber cycle for MgCl₃

The equation for the enthalpy change of formation this time is

\[ \ce{Mg(s) + 3/2 Cl_2(g) \rightarrow MgCl_3 (s)} \nonumber \]

So how does that change the numbers in the Born-Haber cycle this time?

• You need to add in the third ionization energy of magnesium, because you are making a 3+ ion.
• You need to multiply the atomization enthalpy of chlorine by 3, because you need 3 moles of gaseous chlorine atoms.
• You need to multiply the electron affinity of chlorine by 3, because you are making 3 moles of chloride ions.
• You again need a different value for lattice enthalpy.

	kJ
atomization enthalpy of Mg	+148
1st IE of Mg	+738
2nd IE of Mg	+1451
3rd IE of Mg	+7733
atomization enthalpy of Cl (x 3)	+366
electron affinity of Cl (x 3)	-1047
lattice enthalpy	-5440
calculated ΔHf	+3949

This time, the compound is hugely energetically unstable, both with respect to its elements, and also to other compounds that could be formed. You would need to supply nearly 4000 kJ to get 1 mole of MgCl₃ to form! Look carefully at the reason for this. The lattice enthalpy is the highest for all these possible compounds, but it is not high enough to make up for the very large third ionization energy of magnesium. Why is the third ionization energy so big? The first two electrons to be removed from magnesium come from the 3s level. The third one comes from the 2p. That is closer to the nucleus, and lacks a layer of screening as well - and so much more energy is needed to remove it. The 3s electrons are screened from the nucleus by the 1 level and 2 level electrons. The 2p electrons are only screened by the 1 level (plus a bit of help from the 2s electrons).

Conclusion

Magnesium chloride is MgCl₂ because this is the combination of magnesium and chlorine which produces the most energetically stable compound - the one with the most negative enthalpy change of formation.

Theoretical Estimates of Lattice Energies

Let's assume that a compound is fully ionic. Let's also assume that the ions are point charges - in other words that the charge is concentrated at the center of the ion. By doing physics-style calculations, it is possible to calculate a theoretical value for what you would expect the lattice energy to be. Calculations of this sort end up with values of lattice energy, and not lattice enthalpy. If you know how to do it, you can then fairly easily convert between the two.

There are several different equations, of various degrees of complication, for calculating lattice energy in this way. There are two possibilities:

• There is reasonable agreement between the experimental value (calculated from a Born-Haber cycle) and the theoretical value. Sodium chloride is a case like this - the theoretical and experimental values agree to within a few percent. That means that for sodium chloride, the assumptions about the solid being ionic are fairly good.
• The experimental and theoretical values do not agree. A commonly quoted example of this is silver chloride, AgCl. Depending on where you get your data from, the theoretical value for lattice enthalpy for AgCl is anywhere from about 50 to 150 kJ mol^-1 less than the value that comes from a Born-Haber cycle. In other words, treating the AgCl as 100% ionic underestimates its lattice enthalpy by quite a lot.

The explanation is that silver chloride actually has a significant amount of covalent bonding between the silver and the chlorine, because there is not enough electronegativity difference between the two to allow for complete transfer of an electron from the silver to the chlorine. Comparing experimental (Born-Haber cycle) and theoretical values for lattice enthalpy is a good way of judging how purely ionic a crystal is.

Problems

Exercise \(\PageIndex{1}\)

Find the lattice energy of KF(s).
Note: Values can be found in standard tables.

Answer

Lattice Energy= [-436.68-89-(0.5*158)-418.8-(-328)] kJ/mol= -695.48 kJ/mol

Exercise \(\PageIndex{2}\)

Find the lattice energy of MgCl₂(s).

Answer

Lattice Energy= [-641.8-146-243-(737.7+1450.6)-(2*-349)] kJ/mol= -2521.1 kJ/mol

Exercise \(\PageIndex{3}\)

Which one of the following has the greatest lattice energy?

1. MgO
2. NaC
3. LiCl
4. MgCl₂

Answer

MgO. It has ions with the largest charge.

Exercise \(\PageIndex{4}\)

Which one of the following has the greatest Lattice Energy?

NaCl

1. CaCl₂
2. AlCl₃
3. KCl

Answer

AlCl₃. According to the periodic trends, as the radius of the ion increases, lattice energy decreases.

References

1. Cheetham, A.K. and P. Day. Solid State Chemistry. Oxford: Clarendon Press, 1992.
2. Jenkins, H. Donald B. "Thermodynamics of the Relationship between Lattice Energy and Lattice Enthalpy." Journal of Chemical Education. Vol. 82, P. 950-952. Coventry, West Midlands, UK: University of Warwick, 2005.
3. Ladd, Mark. Crystal Structures: Lattices and Solids in Stereoview. Chichester: Horwood, 1999.
4. Ladd, Mark. Chemical Bonding in Solids and Fluids. Chichester: Horwood, 1994.
5. Suzuki, Takashi. Free energy and Self-interacting Particles. Boston: Birkhauser, 2005.
6. Ralph, William, F.Geoffrey, and Jeffry. General Chemistry. Ninth ed. New Jersey:Pearson Education, Inc. 2007. p500;513-515.
7. Combs, Leon. "Lattice Energy". Dr. Leon L. Combs. 1999. erkki.kennesaw.edu/genchem8/ge00002.htm
8. Picture of NaCl diagram intro.chem.okstate.edu/1314f0...BornHaber2.GIF
9. Housecroft, Catherine E. and Alan G. Sharpe. Inorganic Chemistry. 3rd ed. England: Pearson Education Limited, 2008.174-175.