5.11: Lattice Energy - Madelung Constants

When determining lattice energy, there are many factors to be considered such as the covalent character and the electron-electron interactions in ionic solids. For simplicity, let us consider ionic solids to be a collection of cations and anions. In this simple view, the appropriate number of cations and anions come together to form a solid. The cations experience attraction to the anions and repulsion from the other cations. The closer the cation is to an anion, the stronger the degree of attraction between the cation and anion. Likewise, the closer the cation is to another cation, the stronger the repulsive force between the two positively charge ions. The Madelung constant takes in to account the total attractive and repulsive forces between all ions in a solid; it accounts for the differences in attractive and repulsive forces that result from the distance between ions. It is a property of the crystal structure and depends on the type of lattice, the distance between anions and cations, and the volume of the unit cell.

The Madelung constant is incorporated into the Born-Landé equation, which is used to calculate the lattice energy of a compound. The Born-Landé equation is a concept originally formulated in 1918 by the scientists Born and Landé. This expression takes into account Coulomb attractions between ions and the Born repulsive interactions between ions. Using the Madelung constant, this equation considers how the attractive and repulsive forces differ depending on the distance between ions.

Madelung Constants

1D Crystal

Before considering a three-dimensional crystal lattice, we shall discuss the calculation of the energetics of a linear chain of ions of alternate signs (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): A hypothetical one-dimensional \(\ce{NaCl}\) lattice.

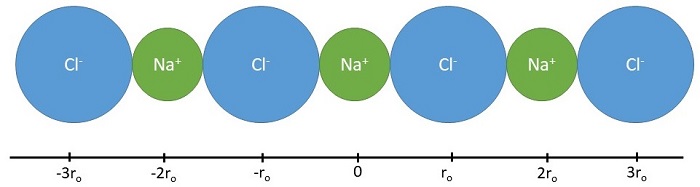
Let sodium cation in the middle (at \(x=0\)) be the reference and let \(r_0\) be the shortest distance between adjacent ions (the sum of ionic radii). The energy of attraction (Coulomb energy) between this sodium cation and all others in this 1D lattice can be calculated by summing the energy of attraction for ions in the same "shells" (at the same distance or proximity).

• Nearest Neighbors (first shell): The sodium cation has two negative chloride ions as its neighbors on either side at \(\pm r_0\) so the Coulombic energy of these interactions is \[ \underbrace{ \dfrac{-e^2}{4 \pi \epsilon_o r_o}}_{\text{left chloride ion}} + \underbrace{ \dfrac{-e^2}{4 \pi \epsilon_o r_o}}_{\text{right chloride ion}} = - \dfrac{2e^2}{4 \pi \epsilon_o r_o} \label{eq1}\]
• Next Nearest Neighbors (second shell): Similarly the repulsive energy due to the next two positive sodium ions at a distance of \(2r_0\) is \[ \underbrace{ \dfrac{+e^2}{4 \pi \epsilon_o (2r_o)}}_{\text{left sodium ion}} + \underbrace{ \dfrac{+e^2}{4 \pi \epsilon_o (2r_o)}}_{\text{right sodium ion}} = + \dfrac{2e^2}{4 \pi \epsilon_o (2r_o)} \label{eq2}\]
• Next Next Nearest Neighbors (third shell): The attractive Coulomb energy due to the next two chloride ions neighbors at a distance \(3r_0\) is \[ \underbrace{ \dfrac{-e^2}{4 \pi \epsilon_o (3r_o)}}_{\text{left chloride ion}} + \underbrace{ \dfrac{-e^2}{4 \pi \epsilon_o (3r_o)}}_{\text{right chloride ion}} = - \dfrac{2e^2}{4 \pi \epsilon_o (3r_o)} \label{eq3}\]

and so on. Thus the total energy due to all the ions in the linear array is

\[ E = - \dfrac{2e^2}{4 \pi \epsilon_o r_o} + \dfrac{2e^2}{4 \pi \epsilon_o (2r_o)} - \dfrac{2e^2}{4 \pi \epsilon_o (3r_o)} - \ldots\]

or

\[ E= \dfrac{e^2}{4 \pi \epsilon_o r_o} \left[ 2 \left (1 -\dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots \right) \right] \label{eq6}\]

We can use the following Maclaurin expansion

\[ \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}- \frac{x^3}{4} + \cdots\]

to simplify the sum in the parenthesis of Equation \ref{eq6} as \(\ln (1+ 1)\) to obtain

\[ \begin{align} E &= \dfrac{e^2}{4 \pi \epsilon_o r_o} \left[ 2 \ln 2 \right] \label{eq7} \\[4pt] &= \dfrac{e^2}{4 \pi \epsilon_o } M \end{align} \]

The first factor of Equation \ref{eq7} is the Coulomb energy for a single pair of sodium and chloride ions, while the \(2 \ln 2\) factor is the Madelung constant (\(M \approx 1.38 \)) per molecule. The Madelung constant is named after Erwin Madelung and is a geometrical factor that depends on the arrangement of ions in the solid. If the lattice were different (when considering 2D or 3D crystals), then this constant would naturally differ.

3D Crystal

In three dimensions the series does present greater difficulty and it is not possible to sum the series conveniently as in the case of one-dimensional lattice. As an example, let us consider the the \(\ce{NaCl}\) crystal. In the following discussion, assume \(r\) be the distance between \(\ce{Na^{+}}\) and \(\ce{Cl^-}\) ions. The nearest neighbors of \(\ce{Na^{+}}\) are six \(\ce{Cl^-}\) ions at a distance 1r, 12 \(\ce{Na^{+}}\) ions at a distance 2r, eight \(\ce{Cl^-}\) ions at 3r, six \(\ce{Na^{+}}\) ions at 4r, 24 \(\ce{Na^{+}}\) ions at 5r, and so on. Thus, the electrostatic potential of a single ion in a crystal by approximating the ions by point charges of the surrounding ions:

\[ E_{ion-lattice} = \dfrac{Z^2e^2}{4\pi\epsilon_or} M \label{12.5.4}\]

For NaCl is a poorly converging series of interaction energies:

\[ M= \dfrac{6}{1} - \dfrac{12}{2} + \dfrac{8}{3} - \dfrac{6}{4} + \dfrac{24}{5} ... \label{21.5.5}\]

with

• \(Z\) is the number of charges of the ions, (e.g., 1 for NaCl),
• \(e\) is the charge of an electron (\(1.6022 \times 10^{-19}\; C\)),
• \(4\pi \epsilon_o\) is 1.11265x10^-10 C²/(J m).

Derived Values

The Madelung constant depends on the structure type and Equation \(\ref{21.5.5}\) is applicable only for the sodium chloride (ei.g, rock salt) lattice geometry. Other values for other structural types are given in Table \(\PageIndex{1}\). \(A\) is the number of anions coordinated to cation and \(C\) is the numbers of cations coordinated to anion.

Table \(\PageIndex{1}\): Madelung Constants

Compound	Crystal Lattice	M	A : C	Type
NaCl	NaCl	1.74756	6 : 6	Rock salt
CsCl	CsCl	1.76267	6 : 6	CsCl type
CaF2	Cubic	2.51939	8 : 4	Fluorite
CdCl2	Hexagonal	2.244
MgF2	Tetragonal	2.381
ZnS (wurtzite)	Hexagonal	1.64132
TiO2 (rutile)	Tetragonal	2.408	6 : 3	Rutile
bSiO2	Hexagonal	2.2197
Al2O3	Rhombohedral	4.1719	6 : 4	Corundum
A is the number of anions coordinated to cation and C is the numbers of cations coordinated to anion.

The Born-Landé Equation

There are other factors to consider for the evaluation of lattice energy and the treatment by Max Born and Alfred Lande led to the formula for the evaluation of lattice energy for a mole of crystalline solid. The Born–Landé equation (Equation \(\ref{21.5.6}\)) is a means of calculating the lattice energy of a crystalline ionic compound and derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term

\[ U= \dfrac{N_A M Z^2e^2}{4\pi \epsilon_o r} \left( 1 - \dfrac{1}{n} \right) \label{21.5.6}\]

where

• \(N_A\) is Avogadro constant;
• \(M\) is the Madelung constant for the lattice
• \(z^+\) is the charge number of cation
• \(z^−\) is the charge number of anion
• \(e\) is elementary charge, 1.6022×10⁻¹⁹ C
• \(ε_0\) is the permittivity of free space
• \(r_0\) is the distance to closest ion

• \(n\) is the Born exponent that is typically between 5 and 12 and is determined experimentally. \(n\) is a number related to the electronic configurations of the ions involved (Table \(\PageIndex{2}\)).

Table \(\PageIndex{2}\): \(n\) values for select solids

Atom/Molecule	n
He	5
Ne	7
Ar	9
Kr	10
Xe	12
LiF	5.9
LiCl	8.0
LiBr	8.7
NaCl	9.1
NaBr	9.5

Derivation of the Born-Landé Equation

To solve for the Born-Landé equation, you must have a basic understanding of lattice energy:

• Lattice energy decreases as you go down a group (as atomic radii goes up, lattice energy goes down).
• Going across the periodic table, atomic radii decreases, therefore lattice energy increases.

The Born-Landé equation was derived from these two following equations. the first is the electrostatic potential energy:

\[ \Delta U = - \dfrac{N_A M\left | Z^+ \right | \left | Z^- \right |e^2}{4\pi\epsilon_o r} \label{1} \]

with

• \(M_A\) is Avogadro's constant (\(6.022 \times 10^{23}\))
• \(M\) is the Madelung Constant (a constant that varies for different structures)
• \(e\) is the charge of an electron (\(1.6022 \times 10^{-19}\) C)
• \(Z^+\) is the cation charge
• \(Z^-\) is the anion charge
• \(\epsilon_o\) is the permittivity of free space

The second equation is the repulsive interaction:

\[ \Delta U = \dfrac{N_A B}{r^n} \label{2} \]

with

• \(B\) is the repulsion coefficient and
• \(n\) is the Born Exponent (typically ranges between 5-12) that is used to measure how much a solid compresses

These equations combine and simplify to form the Born-Landé equation:

\[ \Delta U (0K) = \dfrac{N_A M\left | Z^+ \right | \left | Z^- \right |e^2}{4\pi\epsilon_or_o} \left ( 1- \dfrac{1}{n} \right) \label{3} \]

with

• \(r_0\) is the closest ion distance

Problems

Exercise \(\PageIndex{1}\)

Which compound has the greatest lattice energy?

• AlF₃
• NACl
• LiF
• CaCl₂

Answer

This question requires basic knowledge of lattice energy. Since F₃ gives the compound a +3 positive charge and the Al gives the compound a -1 negative charge, the compound has large electrostatic attraction. The bigger the electrostatic attraction, the greater the lattice energy.

Exercise \(\PageIndex{2}\)

Estimate the lattice energy for \(\ce{NaCl}\).

Answer

Using the values giving in the discussion above, the estimation is given by

\[\begin{align*} U_{NaCl} &= \dfrac{(6.022 \times 10^{23} /mol) (1.74756 ) (1.6022 \times 10 ^{-19})^2}{ 4\pi \, (8.854 \times 10^{-12} C^2/m ) (282 \times 10^{-12}\; m)} \left( 1 - \dfrac{1}{9.1} \right) \nonumber \\[4pt] &= - 766 \,kJ/mol\nonumber \end{align*} \nonumber\]

Much more should be considered in order to evaluate the lattice energy accurately, but the above calculation leads you to a good start. When methods to evaluate the energy of crystallization or lattice energy lead to reliable values, these values can be used in the Born-Hable cycle to evaluate other chemical properties, for example the electron affinity, which is really difficult to determine directly by experiment.