1.18: The Effects of Shielding on Periodic Properties

Estimated Time to Read: 8 min

Z_eff modulates attraction

A modified form of Coulomb's Law is given in Equation \(\PageIndex{1}\), where \(e\) is the charge of an electron, Z_eff is the effective nuclear charge experienced by that electron, and \(r\) is the radius (distance of the electron from the nucleus).

Equation \(\PageIndex{1}\):

\[ F_{eff}=k \dfrac{ Z_{eff} e^2}{r^2} \nonumber \]

This formula suggests that if we can estimate Z_eff, then we can predict the attractive force experienced by and the energy of an electron in a multi-electron atom. The attraction of the nucleus to the valence electrons determines the atomic radius, ionization energy, and electron affinity. The stronger the attraction, and the stronger Z_eff, the closer the electrons are pulled toward the nucleus. This in turn results in a smaller size, higher ionization energy, and higher electron affinity.

The Lanthanide Contraction describes the atomic radius trend that the Lanthanide series exhibits. Another important feature of the The Lanthanide Contraction is the 5s and 5p orbitals penetrate the 4f sub-shell so the 4f orbital is not shielded from the increasing nuclear change, which causes the atomic radius of the atom to decrease. This decrease in size continues throughout the series.

Atomic Radius

Atomic radius generally decreases from left to right across a period of elements. As the nuclear charge (Z) increases, the effective nuclear charge (Z*) of the valence electrons also increases. However, with each addition of a proton there is an addition of an electron. The electrons are added into the valence shell and weakly shielded by the other electrons in the valence shell. Therefore, as Z increases, Z_eff increases more gradually due to shielding. The observed change in atomic radius is a balance of a compression caused by increasing Z and an expansion in the number of electrons. As a result, the atomic radius decreases gradually across a period.

Atomic size generally increases going down a group. As valence electrons occupy higher level shells due to the increasing quantum number (n), size increases despite the fact that Z and Z* are increasing going down the group.

Scandide Contraction

The Scandide Contraction is an atomic radius trend experienced by the d-block elements. Normally atomic radius decreases significantly as nuclear charge increases across a period of the periodic table. In the transition metal elements, the atomic radii only decreases slightly as compared to decreases across the s or p block. D-block elements have the same number of s orbital electrons and only differing in the number of d orbital electrons. The d orbital electrons are inner shell electrons and each additional electron is added to the same shell and subshell. The d orbital electrons are poorly shielding compared to the s and p orbital electrons so effective nuclear charge increases more rapidly across the d-block, resulting in a smaller change in the atomic radius across the period.

Lanthanide Contraction

The Lanthanide series is in the f-block of the periodic table and includes elements 57-70 (La-Yb). As expected based on the periodic trend, the atomic radius of these elements decreases as the atomic number increases (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Atomic radius decreases as the atomic number increases across the Lanthanide Series. [LibreText]

Figure \(\PageIndex{2}\) shows the atomic radii of the first three rows of transition metal elements. Consider the elements with atomic numbers 23, 41, and 73, which are in the same column of the periodic table. The elements 23 and 41 they have a large difference in atomic radii, but the elements 41 and 73 have only a small difference in atomic radii. In general for d-block elements, the atomic radii differ greatly between the Row 1 and Row 2 elements, but the atomic radii differ little between Row 2 and Row 3 elements. This is deviation in the trend is caused by the introduction of 4f electrons in Row 3 and is known as Lanthanide Contraction. As a reminder, s orbitals are the most effective at shielding, followed by the p and d orbitals with the f orbitals being the least effective. The Lanthanide Contraction is the result of the poor shielding effect of the 4f electrons. Because the 4f electrons are poorly shielding, the 5d valence electrons experience a greater effective nuclear charge than would otherwise be expected. When shielding is poor, the positively charged nucleus has a greater attraction to the electrons, and atomic radius decreases more rapidly as the atomic number increases.

Row 1 3d Elements

Row 2, 4d Elements

Row 3, 5d Elements

Figure \(\PageIndex{2}\): Atomic radii of transition metals elements in Period 4 (left), Period 5 (center), and Period 6 (right) [LibreText]

The Lanthanide Contraction can be seen by further comparing the elements with f electrons and those without f electrons in the d block. Pd and Pt are such elements. Pd has 4d electrons while Pt has 5d and 4f electrons. These 2 elements have roughly the same atomic radius. This is due to Lanthanide Contraction and shielding. While we would expect Pt to have a significantly larger radius because more electrons and protons are added, it does not because the 4f electrons are poor at shielding. When the shielding is not good there will be a greater nuclear charge, thus pulling the electrons in closer, resulting in a smaller than expected radius.

Ionization Energy

Ionization energy is the energy required to remove an electron from a neutral gaseous atom. Across a period, the number of protons and the effective nuclear charge increase. As a result, the atomic radius decreases. If we consider Equation 1, increasing effective charge and decreasing radii results in greater attractive forces by the nucleus for electrons. Thus, greater energy is required for an electron to overcome the attractive force of the nucleus and the ionization energy increases.

In general, ionization energies increase from left to right and decrease down a group; however, there are variations in these trends that would be expected from the effects of penetration and shielding.

• Across a period: As Z_eff increases across a period, the ionization energy of the elements generally increases from left to right. However there are breaks or variation in the trends in the following cases:

• IE is especially low when removal of an electron creates a newly empty p subshell (examples include B, Al, Sc)
• IE energy is especially low where removal of an electron results in a half-filled p or d subshell (examples include O, S)
• IE increases more gradually across the d- and f-subshells compared to s- and p- subshells. This is because d- and f- electrons are weakly penetrating and experience especially low Z_eff.

• From one period to the next: There is an especially large decrease in IE with the start of every new period (from He to Li or from Ne to Na for example). This is consistent with the idea that IE is especially low when removal of an electron creates a newly empty s-subshell.
• Noble gases: The noble gases posses very high ionization energies. Note that helium has the highest ionization energy of all the elements.
• Down a group: Although Z_eff increases going down a group, there is no reliable trend in IE going down any group; in some cases IE increases going down a group, while in other cases IE decreases going down a group.

Trends in Electron Affinity

Electron affinity is the change in energy when an electron is added to a neutral gaseous atom. The trends in electron affinity mimic the trends in ionization energy.

• Across a period: Similar to ionization energy, EA generally increases (more negative, more exothermic)across a row of the periodic table; this observation is consistent with the increase in effective nuclear charge (Z_eff) from left to right across a period. However, there are variations across a period that are similar to variations in ionization energy and that can be explained by shielding, penetration, and electron configuration.
• Down a group: Like the case of ionization energy trends, EA does not consistently decrease going down a column of the periodic table despite the fact that Z_eff increases down a group.

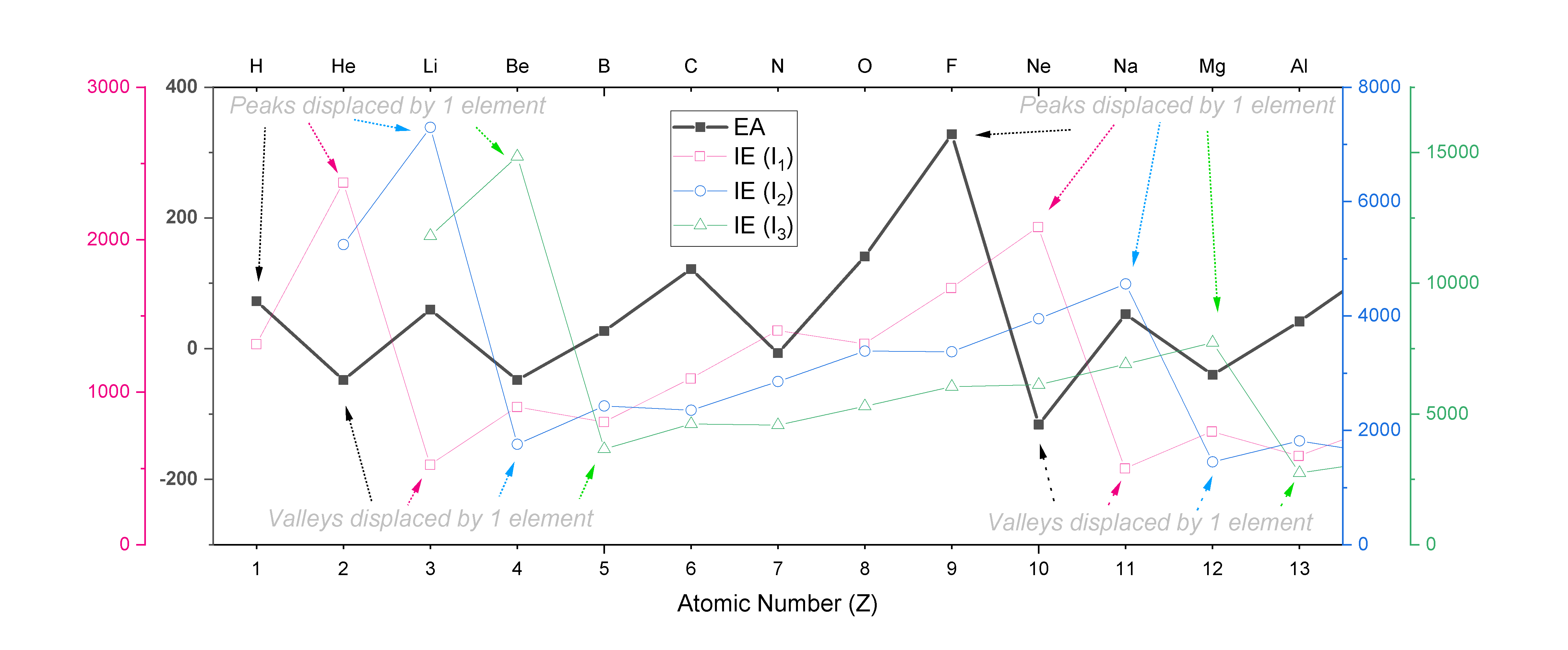
The trend in EA follows a zig-zag pattern similar to the one seen with ionization energies, except that it is displaced by one unit from the trend in IE₁, two units from IE₂, and so on. For example, EA peaks at F, while IE₁ peaks at Ne, IE₂ peaks at Na, and IE₃ peaks at Mg. A plot of EA for the first 13 elements is shown overlaid on plots of IE₁, IE₂, and IE₃ in Figure \(\PageIndex{3}\), where the shifts in the peaks and valleys within each zig-zag trend are indicated.

Figure \(\PageIndex{3}\): A plot of electron affinity (the zeroth ionization energy) is overlaid on plots of the first (IE₁), second (IE₂), and third (IE₃) ionization energies. Each plot is shown using separate y-axes. Trends in EA are similar to those in ionization energies, except that the peaks and valleys of the trends are shifted by one unit, as indicated. These plots are shown in units of kJ/mole. (CC-BY-NC-SA; Kathryn Haas)

Problems

Exercise \(\PageIndex{1}\)

Compare trends in Z* and atomic size. Explain how and why atomic size depends on Z_eff.

Answer

On the periodic table, atomic radius generally decreases across the periods (left to right) and increases down the groups. As atomic number increases across the periodic table, nuclear charge (Z) increases and Z* increases. In turn, the atomic radius decreases because the higher nuclear charge (and thus higher Z*) pulls electrons closer to the nucleus. Atomic radius increases down the periodic table because the shell number increases. Despite an increase in Z* going down the periodic table, larger atomic radii result from electrons occupying higher shells.

 

Exercise \(\PageIndex{2}\)

Compare trends in Z_eff and ionization energy. Explain how and why ionization energy depends on Z_eff.

Answer

Ionization energies (IE) are inversely related to atomic radius; IE increases across the periods and decreases down the groups. Since the nucleus holds valence electrons more strongly (due to higher Z*) across the periods, IE increases because valence electrons are harder to remove. Down the periodic table, larger atomic radii cause electrons in valence orbitals to be shielded by core electrons. Recall that shielding reduces the nuclear charge available to electrons in higher orbital levels, resulting in a lower Z*. With more shielding and lower Z*, the valence electrons are held less tightly by the nucleus such that ionization energy decreases (i.e., valence electrons are easier to remove).

Exercise \(\PageIndex{3}\)

What is the cause of Lanthanide Contraction?

Answer

The Lanthanide Contraction is caused by a poor shielding effect of the 4f electrons

Exercise \(\PageIndex{4}\)

Which element has a greater atomic radius Gd or Tb and why?

Answer

Gd because as atomic number increases, the atomic radius decreases..

Exercise \(\PageIndex{5}\)

Which element has a smaller atomic radius Dy or Yb and why?

Answer

Yb because it has a larger atomic number.

Exercise \(\PageIndex{6}\)

Why do elements in Rows 2 and 3 that are in the same column have similar atomic radii?

Answer

Because the elements in Row 3 have 4f electrons. These electrons are do not shield good, causing a greater nuclear charge. This greater nuclear charge has a greater pull on the electrons.

Exercise \(\PageIndex{7}\)

Place the following elements in order of increasing atomic radius: Eu, Ce, Pr, Ho.

Answer

Ho, Eu, Pr, Ce

References

1. Petrucci, Harwood, Herring, and Madura. General Chemistry Principles & Modern Applications. 9th ed. Prentice Hall. Print.
2. Cotton, Simon. Lanthanide and Actinide Chemistry. Wiley. Print.
3. Electron Affinity (data page), Wikipedia. en.Wikipedia.org/wiki/Electron_affinity_(data_page) Accessed 12/3/19.