1.17: Periodic Trends and Effective Nuclear Charge

Estimated Time to Read: 3 min

Idealized Values for Z_eff

Slater's rules are a set of simple rules for predicting \(S\) and Z_eff based on empirical evidence from quantum mechanical calculations. In other words, the Z_eff calculated from Slater's rules are approximate values. The values considered to be the most accurate are derived from quantum mechanical calculations directly. You can find these values in Figure \(\PageIndex{1}\) for convenience:

Figure \(\PageIndex{1}\): Z_eff values calculated by Clementi et al. in 1963 and 1967 that are consistent with SCF Calculations. [Wikipedia: Effective Nuclear Charge]

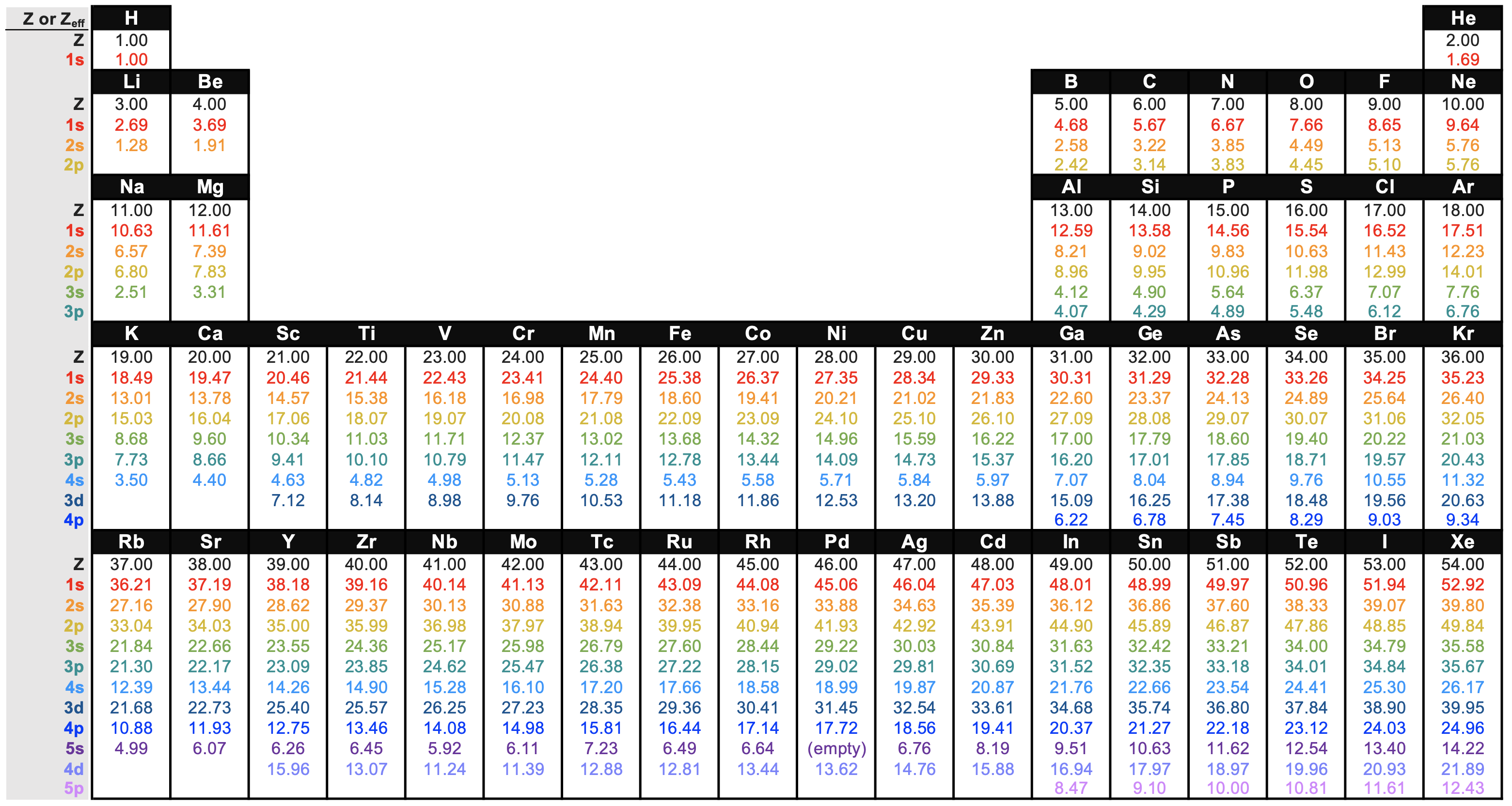
General Periodic Trends in Ze_ff

The data from Figure \(\PageIndex{1}\) is plotted below in Figure \(\PageIndex{2}\). Close inspection of Figure \(\PageIndex{2}\) shows that there are some predictable trends in Z_eff. The Z_eff for electrons in a given shell and subshell generally increase as atomic number increases; this trend holds true going across the periodic table and down the periodic table. You can see this trend as the positive slope in each series in Figure \(\PageIndex{2}\). There is one obvious exception in Period 5 in elements 39 (Y) to 41. For Nb, the Z_eff of the 4s electrons actually decreases as atomic number increases. There is also an exception between Y and Zr in the 3d subshell, and between Tc and Ru in the 5s subshell.

Figure \(\PageIndex{2}\): The Z_eff values for electrons in each subshell of the first 54 elements (H to Xe). Each subshell is plotted as a different series (see legend) and the valence shell is highlighted by a solid black line with open circles. (CC-BY-NC-SA, LibreText)

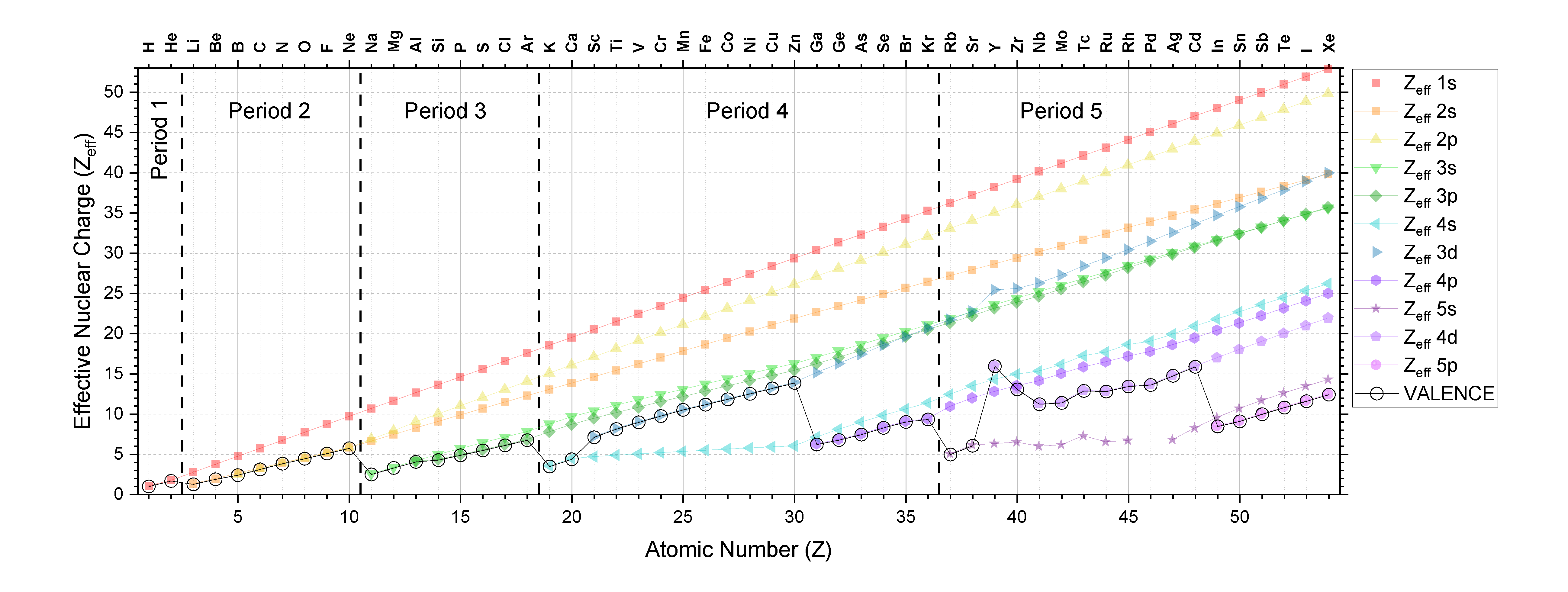
Trends in Z_eff of Valence Electrons

It is useful to understand trends Z_eff for the valence electrons specifically because the valence electrons determine atomic/ionic properties and chemical reactivity. The trends in the Z_eff of the valence electrons are not simple because as atomic number increases, the valence shell and/or subshell also change. The valence Z_eff is indicated in Figure \(\PageIndex{2}\) as a black line with open circles.

Down a column of the periodic table, the Z_eff of the valence electrons increases. This is a simple trend because type of subshell is consistent and there is an increase only in shell and in atomic number, Z. This trend is best illustrated by inspection of Figure \(\PageIndex{1}\).

Across a row of the periodic table, generally Z_eff of the valence electrons increases across a period, but the trend does depend on shell and subshell.

• Periods 1-3 (s and p subshells only): The valence electron shell is constant as Z increases and the subshell changes from s to p. There is a gradual increase in valence Z_eff.
• Periods 4 and 5 (s, p, and d subshells): The valence shell and subshell change as atomic number increases. The Z_eff of the valence electrons generally increases going across a period as long as the subshell does not change. (There is an exception within the 4d subshell for elements 39-44, Y-Ru.) In general, going from an \((n)s\) subshell to an \((n-1)d\) subshell, there is a relatively large increase in valence Z_eff. Going from an \((n-1\)d\) subshell to an \((n)p\) subshell, there is a relatively large decrease in Z_eff.
• Crossing from one period to the next: From Figure \(\PageIndex{2}\), we can see that when Z increases by one proton and the period increases (for example, going from Ne to Na), there is a relatively large decrease in Z_eff. As Z increases by a small interval, the shell number increases, and so the electrons in the valence shell are much farther from the nucleus and are more shielded by the electrons in the lower energy shells.

References

1. Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry: Principles and Modern Applications, Ninth Edition. Pearson Education Inc. Upper Saddle River, New Jersey: 2007.
2. Raymond Chang. Physical Chemistry for Biological Sciences. Sausalito, California: University Science Books, 2005
3. R. S. Mulliken, Electronic Structures of Molecules and Valence. II General Considerations, Physical Review, vol. 41, pp. 49-71 (1932)
4. Anastopoulos, Charis (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 0691135126. http://books.google.com/?id=rDEvQZhpltEC&pg=PA236.

Contributors and Attributions

• Sidra Ayub (UCD), Alan Chu (UCD)
• Emily V Eames (City College of San Francisco)
• Kathryn Haas (Duke)