1.5: Energies of Atomic Orbitals

Estimated Time to Read: 4 min

Single-Electron Atoms

Although we have discussed the shapes of orbitals, we have said little about their comparative energies. We begin our discussion of orbital energies by considering atoms or ions with only a single electron (such as H or He⁺).

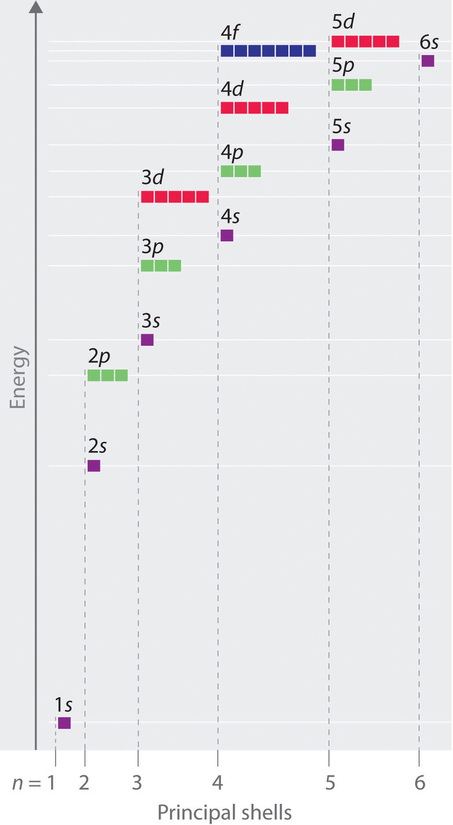
The relative energies of the atomic orbitals with n ≤ 4 for a hydrogen atom are shown in Figure \(\PageIndex{1}\). Note that the orbital energies depend on only the principal quantum number n. Consequently, the energies of the 2s and 2p orbitals of hydrogen are the same; the energies of the 3s, 3p, and 3d orbitals are the same; and so forth. Quantum mechanics predicts that in the hydrogen atom, all orbitals with the same value of n (ex. the three 2p orbitals) are degenerate, meaning that they have the same energy.

The orbital energies obtained for hydrogen using quantum mechanics are exactly the same as the allowed energies calculated by Bohr. In contrast to Bohr’s model, however, which allowed only one orbit for each energy level, quantum mechanics predicts that for the n = 2 shell there are 4 orbitals with different electron density distributions (one 2s and three 2p orbitals). Likewise, for the n = 3 principal shell there are 9 orbitals (one 3s, three 3p, and five 3d orbitals), and for the n = 4 shell there are 16 orbitals (one 4s, three 4p, five 4d, and seven 4f orbitals). Figure \(\PageIndex{1}\) shows that the energy levels become closer and closer together as the value of n increases, as expected because of the 1/n² dependence of orbital energies.

Figure \(\PageIndex{1}\): Orbital energy level diagram for the hydrogen atom with a single electron. Each box corresponds to one orbital. Note that the difference in energy between orbitals decreases rapidly with increasing values of n.

The energies of the orbitals in any species with only one electron can be calculated by a minor variation of Bohr’s equation, which can be extended to other single-electron species by incorporating the nuclear charge \(Z\) (the number of protons in the nucleus):

\[E=−\dfrac{Z^2}{n^2}Rhc \label{6.6.1} \]

In general, both energy and radius decrease as the nuclear charge increases. Thus the most stable orbitals (those with the lowest energy) are those closest to the nucleus. For example, in the ground state of the hydrogen atom, the single electron is in the 1s orbital, whereas in the first excited state, the atom has absorbed energy and the electron has been promoted to one of the n = 2 orbitals. In ions with only a single electron, the energy of a given orbital depends on only n, and all subshells within a principal shell, such as the \(p_x\), \(p_y\), and \(p_z\) orbitals, are degenerate.

Multi-Electron Atoms

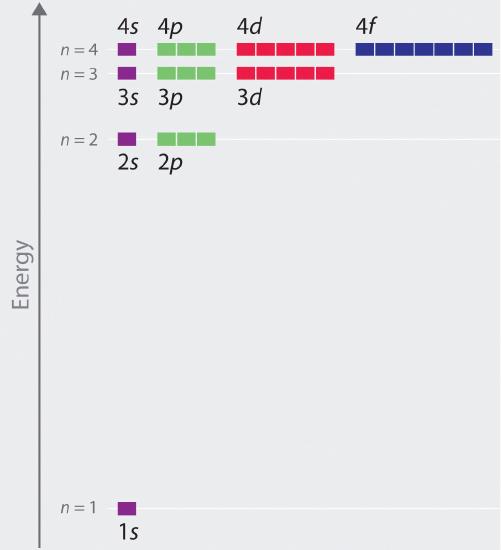
Unlike in hydrogen-like atoms with only one electron, in multielectron atoms the values of quantum numbers n and l determine the energies of an orbital. The energies of the different orbitals for a typical multielectron atom are shown in Figure \(\PageIndex{21}\). Within a given principal shell of a multielectron atom, the orbital energies increase with increasing l. An ns orbital always lies below the corresponding np orbital, which in turn lies below the nd orbital.

These energy differences are caused by the effects of shielding and penetration, the extent to which a given orbital lies inside other filled orbitals. For example, an electron in the 2s orbital penetrates inside a filled 1s orbital more than an electron in a 2p orbital does. Since electrons, all being negatively charged, repel each other, an electron closer to the nucleus partially shields an electron farther from the nucleus from the attractive effect of the positively charged nucleus. Hence in an atom with a filled 1s orbital, the effective nuclear charge (Z_eff) experienced by a 2s electron is greater than the Z_eff experienced by a 2p electron. Consequently, the 2s electron is more tightly bound to the nucleus and has a lower energy, consistent with the order of energies shown in Figure \(\PageIndex{2}\). We will discuss shielding and penetration in more detail in a later section. For now, you should note that the energies of different orbitals in the same shell varies depending on the shapes of the orbitals. As the shapes become more complex, they allow less electron density near the nucleus, which destabilizes the electrons, and increases the energy of the orbital.

Notice in Figure \(\PageIndex{2}\) that the difference in energies between subshells can be so large that the energies of orbitals from different principal shells can become approximately equal. For example, the energy of the 3d orbitals in most atoms is actually between the energies of the 4s and the 4p orbitals.

Figure \(\PageIndex{2}\): Orbital energy level diagram for a typical multielectron atom. Each box corresponds to one orbital.