5.4: The Bohr Atom
- Page ID
- 3507
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas:
- Describe the Thompson, Rutherford, and early planetary models of the atom, and explain why the latter is not consistent with classical physics.
- State the major concepts that distinguished Bohr's model of the atom from the earlier planetary model.
- Give an example of a mechanical standing wave; state the meaning and importance of its boundary conditions.
- Sketch out a diagram showing how the concept of a standing wave applies to the description of the electron in a hydrogen atom.
- What is an atomic line emission spectrum? What is the significance of the continuum region of an emission spectrum? Sketch out a drawing showing the essentials of such a spectrum, including the ionization limit and the continuum.
- Describe the way in which Bohr's quantum numbers explain the observed spectrum of a typical atom.
- Explain the relation between the absorption and emission spectrum of an atom.
Our goal in this unit is to help you understand how the arrangement of the periodic table of the elements must follow as a necessary consequence of the fundamental laws of the quantum behavior of matter. The modern theory of the atom makes full use of the wave-particle duality of matter. In order to develop and present this theory in a comprehensive way, we would require a number of mathematical tools that lie beyond the scope of this course. We will therefore present the theory in a semi-qualitative manner, emphasizing its results and their applications, rather than its derivation.
Models of the atom
Models are widely employed in science to help understand things that cannot be viewed directly. The idea is to imagine a simplified system or process that might be expected to exhibit the basic properties or behavior of the real thing, and then to test this model against more complicated examples and modify it as necessary. Although one is always on shaky philosophical ground in trying to equate a model with reality, there comes a point when the difference between them becomes insignificant for most practical purposes.
The planetary model
The demonstration by Thompson in 1867 that all atoms contain units of negative electric charge led to the first science-based model of the atom which envisaged the electrons being spread out uniformly throughout the spherical volume of the atom. Ernest Rutherford, a New Zealander who started out as Thompson's student at Cambridge, distrusted this "plum pudding" model (as he called it) and soon put it to rest; Rutherford's famous alpha-ray bombardment experiment (carried out, in 1909, by his students Hans Geiger and Ernest Marsden) showed that nearly all the mass of the atom is concentrated in an extremely small (and thus extremely dense) body called the nucleus. This led him to suggest the planetary model of the atom, in which the electrons revolve in orbits around the nuclear "sun".
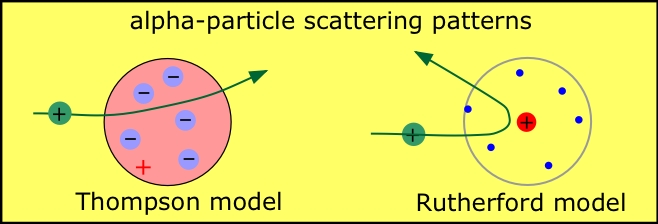
Even though the planetary model has long since been discredited, it seems to have found a permanent place in popular depictions of the atom, and certain aspects of it remain useful in describing and classifying atomic structure and behavior. The planetary model of the atom assumed that the electrostatic attraction between the central nucleus and the electron is exactly balanced by the centrifugal force created by the revolution of the electron in its orbit. If this balance were not present, the electron would either fall into the nucleus, or it would be flung out of the atom.
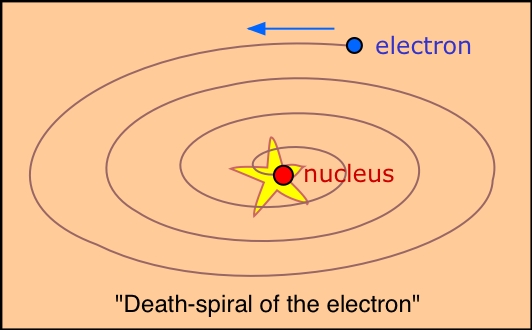
The difficulty with this picture is that it is inconsistent with a well established fact of classical electrodynamics which says that whenever an electric charge undergoes a change in velocity or direction (that is, acceleration, which must happen if the electron circles around the nucleus), it must continually radiate energy. If electrons actually followed such a trajectory, all atoms would act is miniature broadcasting stations. Moreover, the radiated energy would come from the kinetic energy of the orbiting electron; as this energy gets radiated away, there is less centrifugal force to oppose the attractive force due to the nucleus. The electron would quickly fall into the nucleus, following a trajectory that became known as the "death spiral of the electron". According to classical physics, no atom based on this model could exist for more than a brief fraction of a second.
Bohr's Model
Niels Bohr was a brilliant Danish physicist who came to dominate the world of atomic and nuclear physics during the first half of the twentieth century. Bohr suggested that the planetary model could be saved if one new assumption were made: certain "special states of motion" of the electron, corresponding to different orbital radii, would not result in radiation, and could therefore persist indefinitely without the electron falling into the nucleus. Specifically, Bohr postulated that the angular momentum of the electron, mvr (the mass and angular velocity of the electron and in an orbit of radius \(r\)) is restricted to values that are integral multiples of \(h/2\pi\). The radius of one of these allowed Bohr orbits is given by
\[r=\dfrac{nh}{2\pi m u}\]
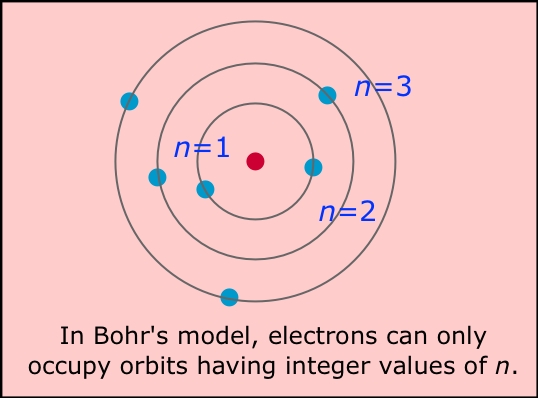
in which h is Planck's constant, m is the mass of the electron, v is the orbital velocity, and n can have only the integer values 1, 2, 3, etc. The most revolutionary aspect of this assumption was its use of the variable integer n; this was the first application of the concept of the quantum number to matter. The larger the value of n, the larger the radius of the electron orbit, and the greater the potential energy of the electron.
As the electron moves to orbits of increasing radius, it does so in opposition to the restoring force due to the positive nucleus, and its potential energy is thereby raised. This is entirely analogous to the increase in potential energy that occurs when any mechanical system moves against a restoring force— as, for example, when a rubber band is stretched or a weight is lifted.
Thus what Bohr was saying, in effect, is that the atom can exist only in certain discrete energy states: the energy of the atom is quantized. Bohr noted that this quantization nicely explained the observed emission spectrum of the hydrogen atom. The electron is normally in its smallest allowed orbit, corresponding to n = 1; upon excitation in an electrical discharge or by ultraviolet light, the atom absorbs energy and the electron gets promoted to higher quantum levels. These higher excited states of the atom are unstable, so after a very short time (around 10—9 sec) the electron falls into lower orbits and finally into the innermost one, which corresponds to the atom's ground state. The energy lost on each jump is given off as a photon, and the frequency of this light provides a direct experimental measurement of the difference in the energies of the two states, according to the Planck-Einstein relationship e = hν.
Vibrations, standing waves and bound states
Bohr's theory worked; it completely explained the observed spectrum of the hydrogen atom, and this triumph would later win him a Nobel prize. The main weakness of the theory, as Bohr himself was the first to admit, is that it could offer no good explanation of whythese special orbits immunized the electron from radiating its energy away. The only justification for the proposal, other than that it seems to work, comes from its analogy to certain aspects of the behavior of vibrating mechanical systems.
Spectrum of a guitar string
In order to produce a tone when plucked, a guitar string must be fixed at each end (that is, it must be a bound system) and must be under some tension. Only under these conditions will a transverse disturbance be countered by a restoring force (the string's tension) so as to set up a sustained vibration. Having the string tied down at both ends places a very important boundary condition on the motion: the only allowed modes of vibration are those whose wavelengths produce zero displacements at the bound ends of the string; if the string breaks or becomes unattached at one end, it becomes silent.
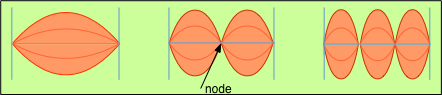
In its lowest-energy mode of vibration there is a single wave whose point of maximum displacement is placed at the center of the string. In musical terms, this corresponds to the fundamental note to which the string is tuned; in terms of the theory of vibrations, it corresponds to a "quantum number" of 1. Higher modes, known as overtones (and in music, as octaves), contain 2, 3, 4 and more points of maximum displacement (antinodes) spaced evenly along the string, separated by points of zero displacement (nodes). These correspond to successively higher quantum numbers and higher energies.
The vibrational states of the string are quantized in the sense that an integral number of antinodes must be present. Note again that this condition is imposed by the boundary condition that the ends of the string, being fixed in place, must be nodes. Because the locations of the nodes and antinodes do not change as the string vibrates, the vibrational patterns are known as standing waves.
A similar kind of quantization occurs in other musical instruments; in each case the vibrations, whether of a stretched string, a column of air, or of a stretched membrane.
Standing waves live in places other than atoms and musical instruments: every time you turn on your microwave oven, a complex set of standing waves fills the interior. What is "waving" here is the alternating electrostatic field as a function of location; the wave patterns are determined by the dimensions of the oven interior and by the objects placed within it. But the part of a pizza that happens to be located at a node would not get very hot, so all microwave ovens provide a mechanical means of rotating either the food (on a circular platform) or the microwave beam (by means of a rotating deflector) so that all parts will pass through high-amplitude parts of the waves.Standing waves in the hydrogen atom
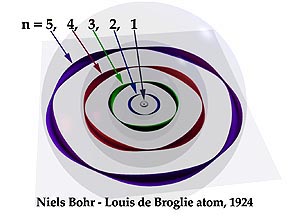
The analogy with the atom can be seen by imagining a guitar string that has been closed into a circle. The circle is the electron orbit, and the boundary condition is that the waves must not interfere with themselves along the circle. This condition can only be met if the circumference of an orbit can exactly accommodate an integral number of wavelengths. Thus only certain discrete orbital radii and energies are allowed, as depicted in the two diagrams below.

Unbound states
If a guitar string is plucked so harshly that it breaks, the restoring force and boundary conditions that restricted its motions to a few discrete harmonically related frequencies are suddenly absent; with no constraint on its movement, the string's mechanical energy is dissipated in a random way without musical effect. In the same way, if an atom absorbs so much energy that the electron is no longer bound to the nucleus, then the energy states of the atom are no longer quantized; instead of the line spectrum associated with discrete energy jumps, the spectrum degenerates into a continuum in which all possible electron energies are allowed. The energy at which the ionization continuum of an atom begins is easily observed spectroscopically, and serves as a simple method of experimentally measuring the energy with which the electron is bound to the atom.
Spectrum of the hydrogen atom
Hydrogen, the simplest atom, also has the simplest line spectrum (line spectra were briefly introduced in the previous chapter.) The hydrogen spectrum was the first to be observed (by Ånders Ångström in the 1860's). Johannn Balmer, a German high school teacher, discovered a simple mathematical formula that related the wavelengths of the various lines that are observable in the visible and near-uv parts of the spectrum. This set of lines is now known as the Balmer Series.
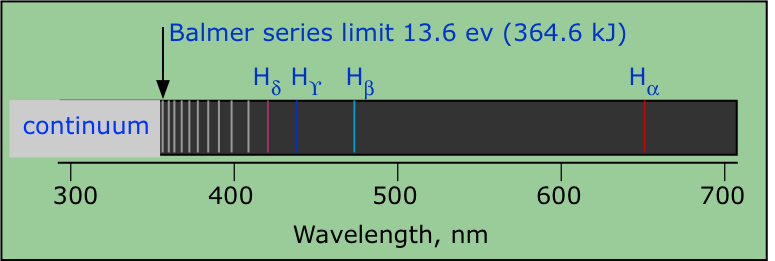
The four lines in the visible spectrum (designated by α through δ) were the first observed by Balmer. Notice how the lines crowd together as they approach the ionization limit in the near-ultraviolet part of the spectrum. Once the electron has left the atom, it is in an unbound state and its energy is no longer quantized. When such electrons return to the atom, they possess random amounts of kinetic energies over and above the binding energy. This reveals itself as the radiation at the short-wavelength end of the spectrum known as the continuum radiation. Other named sets of lines in the hydrogen spectrum are the Lyman series (in the ultraviolet) and the Paschen, Brackett, Pfund and Humphrey series in the infrared.
How the Bohr model explains the hydrogen line spectrum
Each spectral line represents an energy difference between two possible states of the atom. Each of these states corresponds to the electron in the hydrogen atom being in an "orbit" whose radius increases with the quantum number n. The lowest allowed value of n is 1; because the electron is as close to the nucleus as it can get, the energy of the system has its minimum (most negative) value. This is the "normal" (most stable) state of the hydrogen atom, and is called the ground state.
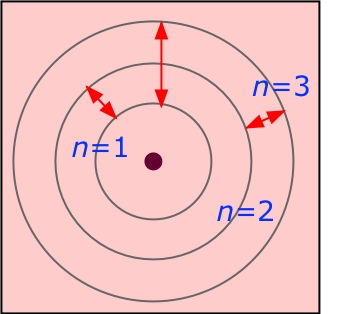
If a hydrogen atom absorbs radiation whose energy corresponds to the difference between that of n=1 and some higher value of n, the atom is said to be in an excited state. Excited states are unstable and quickly decay to the ground state, but not always in a single step. For example, if the electron is initially promoted to the n=3 state, it can decay either to the ground state or to the n=2 state, which then decays to n=1. Thus this single n=1→3 excitation can result in the three emission lines depicted in the diagram above, corresponding to n=3→1, n=3→2, and n=2→1.
If, instead, enough energy is supplied to the atom to completely remove the electron, we end up with a hydrogen ion and an electron. When these two particles recombine (H+ + e– → H), the electron can initially find itself in a state corresponding to any value of n, leading to the emission of many lines.
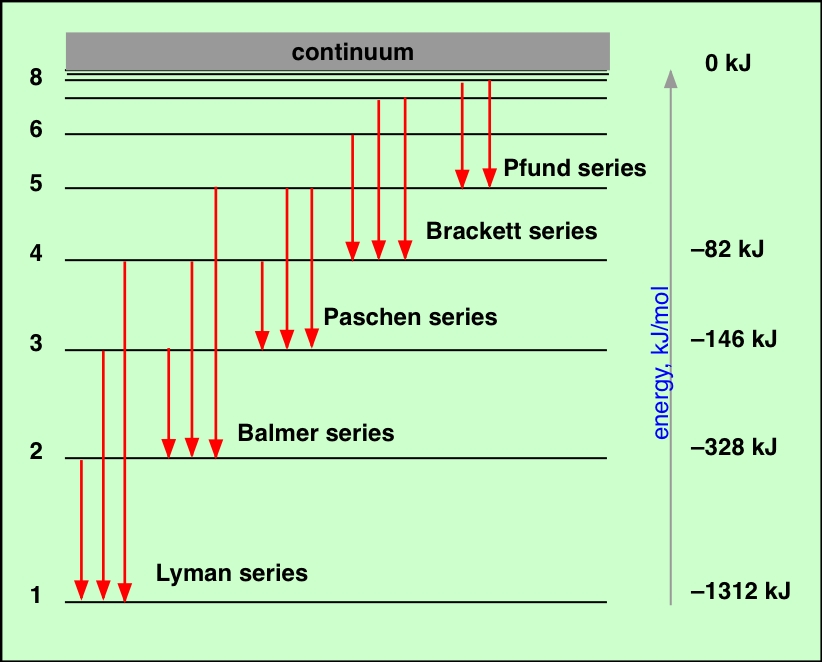
The lines of the hydrogen spectrum can be organized into different series according to the value of n at which the emission terminates (or at which absorption originates.) The first few series are named after their discoverers. The most well-known (and first-observed) of these is the Balmer series, which lies mostly in the visible region of the spectrum. The Lyman lines are in the ultraviolet, while the other series lie in the infrared. The lines in each series crowd together as they converge toward the series limit which corresponds to ionization of the atom and is observed as the beginning of the continuum emission. Note that the ionization energy of hydrogen (from its ground state) is 1312 kJ mol–1. Although an infinite number of n-values are possible, the number of observable lines is limited by our ability to resolve them as they converge into the continuum; this number is around a thousand.
Emission and absorption spectra
The line emission spectra we have been discussing are produced when electrons which had previously been excited to values of n greater than 1 fall back to the n=1 ground state, either directly, or by way of intermediate-n states. But if light from a continuous source (a hot body such as a star) passes through an atmosphere of hydrogen (such as the star's outer atmosphere), those wavelengths that correspond to the allowed transitions are absorbed, and appear as dark lines superimposed on the continuous spectrum.
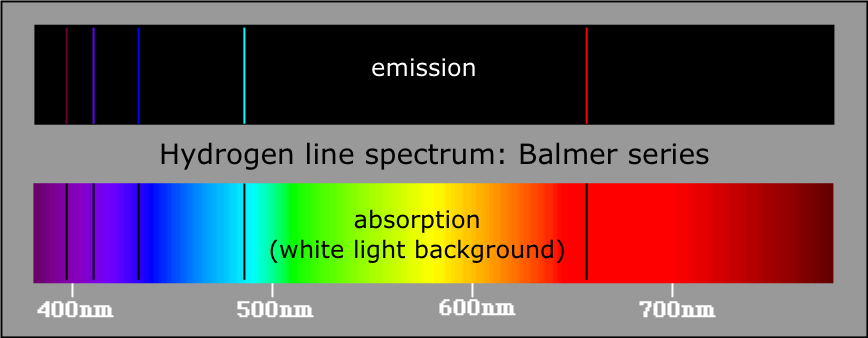
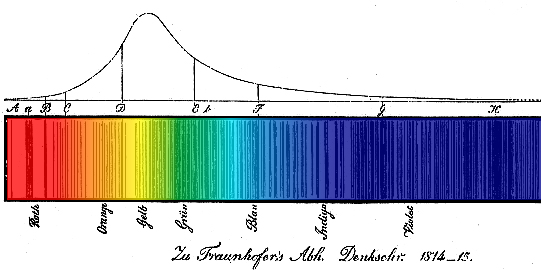
These dark absorption lines were first observed by William Wollaston in his study of the solar spectrum. In 1814, Joseph von Fraunhofner (1787-1826) re-discovered them and made accurate measurements of 814 lines, including the four most prominent of the Balmer lines.