6.3: Classifying Monosaccharides
- Page ID
- 341506
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning Objectives
- Classify monosaccharides based on the carbonyl group.
- Classify monosaccharides based on the number of carbon atoms.
- Distinguish between a D sugar and an L sugar.
Types of Monosaccharides
The naturally occurring monosaccharides contain three to seven carbon atoms per molecule. Monosaccharides of specific sizes may be indicated by names composed of a stem denoting the number of carbon atoms and the suffix -ose. For example, the terms triose, tetrose, pentose, and hexose signify monosaccharides with, respectively, three, four, five, and six carbon atoms.
Monosaccharides are also classified as aldoses or ketoses to indicate the carbonyl-containing group that is present. Those that contain an aldehyde functional group are called aldoses; those containing a ketone functional group on the second carbon atom are ketoses. Combining these classification systems gives general names that indicate both the type of carbonyl group and the number of carbon atoms in a molecule. Thus, monosaccharides are described as aldotetroses, aldopentoses, ketopentoses, ketoheptoses, and so forth. Glucose and fructose are specific examples of an aldohexose and a ketohexose, respectively.

Example \(\PageIndex{1}\)
Draw an example of each type of compound.
-
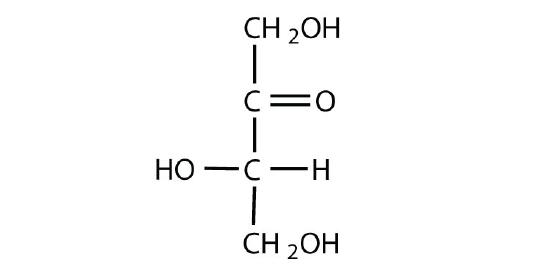
a ketopentose
-
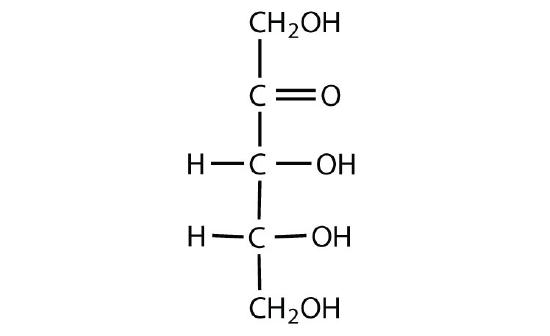
an aldotetrose
Solution
-
The structure must have five carbon atoms with the second carbon atom being a carbonyl group and the other four carbon atoms each having an OH group attached. Several structures are possible, but one example is shown.
-
The structure must have four carbon atoms with the first carbon atom part of the aldehyde functional group. The other three carbon atoms each have an OH group attached. Several structures are possible, but one example is shown.
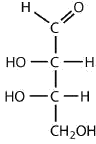
Exercise \(\PageIndex{1}\)
Draw an example of each type of compound.
-
an aldohexose
-
a ketotetrose
Stereochemistry of Monosaccharides
The simplest sugars are the trioses. The possible trioses are shown in part (a) of Figure \(\PageIndex{2}\); glyceraldehyde is an aldotriose, while dihydroxyacetone is a ketotriose. Notice that two structures are shown for glyceraldehyde. These structures are stereoisomers, and hence are isomers having the same structural formula but differing in the arrangement of atoms or groups of atoms in three-dimensional space. If you make models of the two stereoisomers of glyceraldehyde, you will find that you cannot place one model on top of the other and have each functional group point in the same direction. However, if you place one of the models in front of a mirror, the image in the mirror will be identical to the second stereoisomer in part (b) of Figure \(\PageIndex{2}\). Since these molecules are nonsuperimposable mirror images of each other, they represent enantiomers.

A key characteristic of enantiomers is that they have a chiral carbon. If a molecule contains one or more chiral carbons, it is likely to exist as two or more stereoisomers. Dihydroxyacetone does not contain a chiral carbon and thus does not exist as a pair of stereoisomers. Glyceraldehyde, however, has a chiral carbon and exists as a pair of enantiomers. Except for the direction in which each enantiomer rotates plane-polarized light, these two molecules have identical physical properties. One enantiomer has a specific rotation of +8.7°, while the other has a specific rotation of −8.7°.
H. Emil Fischer, a German chemist, developed the convention commonly used for drawing monosaccharides. These structural formulas, known as Fischer projections, use horizontal and vertical lines to indicate the three–dimensional structure of a molecule. The horizontal lines project forward (coming towards you), while the vertical lines project backward (going away from you). Where the lines intersect represents a carbon atom that is usually chiral.
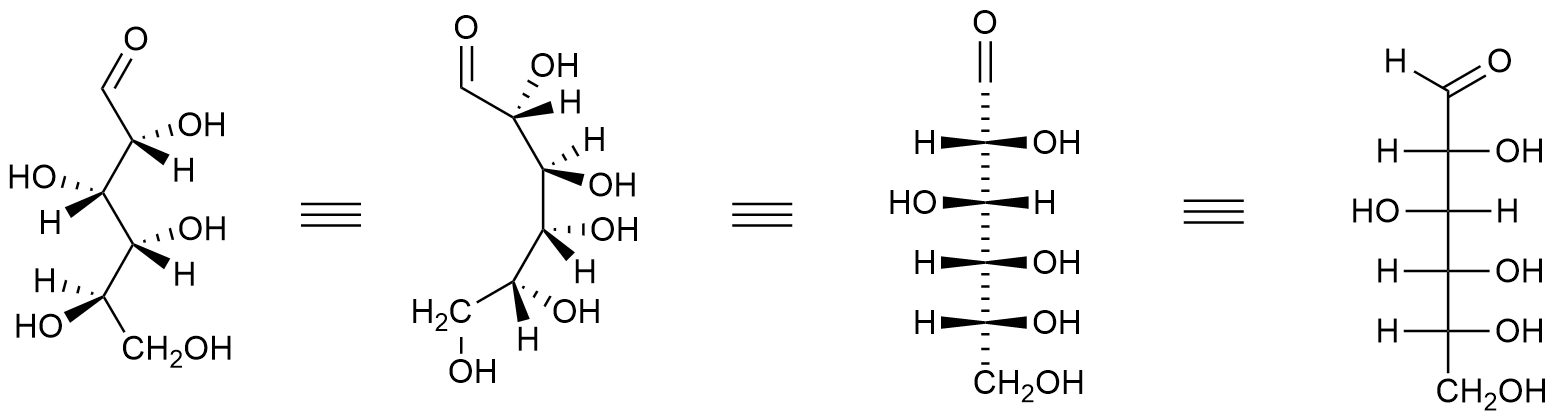
Figure \(\PageIndex{3}\): Projection of Glucose to the Fischer Projection. Choutkaj, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons
When drawing Fischer projections, the aldehyde group is written at the top, and the H and OH groups that are attached to each chiral carbon are written to the right or left. The arrange of the atoms distinguishes one stereoisomer from the other.
The two enantiomers of glyceraldehyde are especially important because monosaccharides with more than three carbon atoms can be considered as being derived from them. Thus, D- and L-glyceraldehyde provide reference points for designating and drawing all other monosaccharides. Sugars whose Fischer projections terminate in the same configuration as D-glyceraldehyde are designated as D sugars; those derived from L-glyceraldehyde are designated as L sugars. D and L designations of sugars are based on the position of the hydroxyl on the chiral carbon farthest from the carbonyl group in the Fischer projection of the molecule. All D-sugars have the –OH on the right side and L-sugars have the –OH on the left side.


Figure \(\PageIndex{4}\): Fischer projections of enantiomers of glucose (left) and fructose (right).
By convention, the penultimate (next-to-last) carbon atom has been chosen as the carbon atom that determines if a sugar is D or L. It is the chiral carbon farthest from the aldehyde or ketone functional group.
D and L sugars of the same monosaccharide are enantiomers of one another (Figure \(\PageIndex{4}\)). When comparing the Fischer projections of monosaccharides, if the arrangement around all of the chiral centers (horizontal lines) are the exact opposite, then the molecules are enantiomers. However, molecules are not “perfect” mirror images are diastereomers. When comparing Fischer projections of monosaccharides, if the arrangement is different at one or more (but not all) chiral centers, then the molecules are diastereomers (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Fischer projections of diastereomers: D-glucose and D-talose.
The arrangement of H and OH around each chiral center gives the identity of the carbohydrate. Since diastereomers have different arrangements, they will also have different names. Since epimers are a type of diastereomers, they will also have dfiferent names. When comparing Fischer projections, if the arrangement is different at only one chiral center, the molecules are epimers. For example, D-glucose and D-galactose are epimers because the molecules are identical, except for the arrangement of the H and OH around carbon 4 Figure \(\PageIndex{6}\).

The general formula for determining the maximum number of stereoisomers of a molecule is 2n, where n is the number of chiral centers present in the molecule. IN the case of glucose, carbons 2, 3, 4, and 5 are chiral centers. Therefore, there are 24 = 2 x 2 x 2 x 2 = 16 stereoisomers of the molecule. Only two can represent enatiomers, while the others would represent diastereomers (or epimers).
Looking Closer: Polarized Light
A beam of ordinary light can be pictured as a bundle of waves; some move up and down, some sideways, and others at all other conceivable angles. When a beam of light has been polarized, however, the waves in the bundle all vibrate in a single plane. Light altered in this way is called plane-polarized light. Much of what chemists know about stereoisomers comes from studying the effects they have on plane-polarized light. In this illustration, the light on the left is not polarized, while that on the right is polarized.
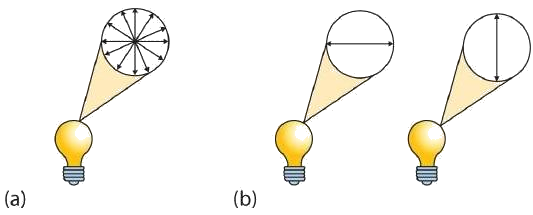
Sunlight, in general, is not polarized; light from an ordinary light bulb or an ordinary flashlight is not polarized. One way to polarize ordinary light is to pass it through Polaroid sheets, special plastic sheets containing carefully oriented organic compounds that permit only light vibrating in a single plane to pass through. To the eye, polarized light doesn’t “look” any different from nonpolarized light. We can detect polarized light, however, by using a second sheet of polarizing material, as shown here.

In the photo on the left, two Polaroid sheets are aligned in the same direction; plane-polarized light from the first Polaroid sheet can pass through the second sheet. In the photo on the right, the top Polaroid sheet has been rotated 90° and now blocks the plane-polarized light that comes through the first Polaroid sheet.
Certain substances act on polarized light by rotating the plane of vibration. Such substances are said to be optically active. The extent of optical activity is measured by a polarimeter, an instrument that contains two polarizing lenses separated by a sample tube, as shown in the accompanying figure. With the sample tube empty, maximum light reaches the observer’s eye when the two lenses are aligned so that both pass light vibrating in the same plane. When an optically active substance is placed in the sample tube, that substance rotates the plane of polarization of the light passing through it, so that the polarized light emerging from the sample tube is vibrating in a different direction than when it entered the tube. To see the maximum amount of light when the sample is in place, the observer must rotate one lens to accommodate the change in the plane of polarization.

Some optically active substances rotate the plane of polarized light to the right (clockwise) from the observer’s point of view. These compounds are said to be dextrorotatory (d) and the direction of rotation is denoted with a positive sign (+). Substances that rotate light to the left (counterclockwise) are said to be levorotatory (l) and the direction of rotation is denoted with a negative sign (−). Achiral compounds are optically inactive because they do not rotate plane-polarized light. Racemic mixtures, mixtures containing a 50:50 mix of both enantiomers, are also optically inactive.
Example \(\PageIndex{2}\)
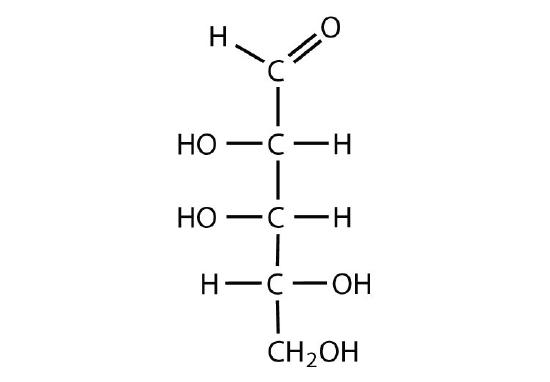
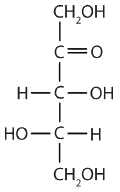
Identify each sugar as an aldose or a ketose and then as a D sugar or an L sugar.
Solution
-
aldose; D sugar. The carbonyl group is on carbon 1 which indicates the presence of an aldehyde. The hydroxyl on the chiral carbon farthest from the carbonyl group is pointing to the right, making it a D-sugar.
-
ketose; L sugar. The carbonyl group is on carbon 2 which indicates the presence of an ketone. The hydroxyl on the chiral carbon farthest from the carbonyl group is pointing to the left, making it an L-sugar.
Exercise \(\PageIndex{2}\)
Identify each sugar as an aldose or a ketose and then as a D sugar or an L sugar.
Summary
- Monosaccharides can be classified based on their chemical composition (number of carbon atoms and/or the type of carbonyl group).
- Fischer projections are commonly used to draw monosaccharides. The intersection of the horizontal and veritical lines represents a carbon, which is typically a chiral center.
- Most monosaccharides contain at least one chiral carbon and can form 2n possible stereoisomers.
- Three types of stereoisomers present in monosaccharides can be identified by comparing the chiral centers in Fischer Projections:
o all opposite = enantiomers
o only 1 opposite = epimers
o more than 1, but less than all opposite = diastereomers - Enantiomers are a specific type of stereoisomers that are mirror images of each other and rotate plane polarized light in opposite directions.