5.5: Relative Strengths of Bases
- Page ID
- 364673
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Assess the relative strengths of bases according to their ionization constants
- Carry out equilibrium calculations for weak acid–base systems
- Calculate the Kb for the conjugate base of a weak acid
Bases act as proton acceptors. When in aqueous solutions, the water solvent can act as the acid that donates the proton to a base. As we did with acids, we can measure the relative strengths of bases by measuring their base-ionization constant (Kb) in aqueous solutions. In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than do weaker bases. A stronger base has a larger ionization constant than does a weaker base. For the reaction of a base, \(\ce{B}\):
\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq),\]
we write the equation for the ionization constant as:
\[K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\]
where the concentrations are those at equilibrium. Again, we do not see water in the equation because water is the solvent and has an activity of 1.
A strong base yields 100% (or very nearly so) of OH− and HB+ when it reacts with water, while a weak base yields a small proportion of hydroxide ions. Soluble ionic hydroxides such as NaOH and Ca(OH)2 are considered strong bases because they dissociate completely when dissolved in water.
Caffeine, C8H10N4O2 is a weak base. What is the value of Kb for caffeine if a solution at equilibrium has [C8H10N4O2] = 0.050 M, \(\ce{[C8H10N4O2H+]}\) = 5.0 × 10−3 M, and [OH−] = 2.5 × 10−3 M?
Solution
At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:
\[\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \nonumber \]
so
\[K_\ce{b}=\ce{\dfrac{[C8H10N4O2H+][OH- ]}{[C8H10N4O2]}}=\dfrac{(5.0×10^{−3})(2.5×10^{−3})}{0.050}=2.5×10^{−4} \]
What is the equilibrium constant for the ionization of the \(\ce{HPO4^2-}\) ion, a weak base:
\[\ce{HPO4^2-}(aq)+\ce{H2O}(l)⇌\ce{H2PO4-}(aq)+\ce{OH-}(aq) \nonumber \]
In a solution containing a mixture of \(\ce{NaH2PO4}\) and \(\ce{Na2HPO4}\) at equilibrium with:
- \([\ce{OH^{−}}] = 1.3 × 10^{−6} M\)
- \(\ce{[H2PO4^{-}]=0.042\:M}\) and
- \(\ce{[HPO4^{2-}]=0.341\:M}\).
- Answer
-
Kb for \(\ce{HPO4^2-}=1.6×10^{−7} \)
The pH of a solution of household ammonia, a 0.950-M solution of NH3, is 11.612. What is Kb for NH3.
- Answer
-
\(K_b = 1.8 × 10^{−5}\)
pH Calculations for Strong and Weak Bases
To determine the pH of a solution containing a strong base, the concentration of hydroxide ions, \(\ce{[OH^-]} \), is used to find the pOH.
\(pOH=-log\ce{[OH^-]} \)
The pH and pOH are related through Kw, and so pH can be determined.
\(pH+pOH=14\)
Weak bases cause only partial ionization. To determine the pH of a weak base solution we must utilize the base ionization constant. The reaction of a base, \(\ce{B}\), is:
\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq),\]
For example, a solution of the weak base trimethylamine, (CH3)3N, in water reacts according to the equation:
\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \nonumber\]
This gives an equilibrium mixture with most of the base present as the nonionized amine. This equilibrium is analogous to that described for weak acids.
We can confirm by measuring the pH of an aqueous solution of a weak base of known concentration that only a fraction of the base reacts with water (Figure \(\PageIndex{1}\)). The remaining weak base is present as the unreacted form. The equilibrium constant for the ionization of a weak base, \(K_b\), is called the ionization constant of the weak base, and is equal to the reaction quotient when the reaction is at equilibrium. For trimethylamine, at equilibrium:
\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}} \nonumber\]
Table \(\PageIndex{1}\) contains ionization reactions and base ionization constants for select weak bases.
| Ionization Reaction | Kb at 25 °C |
|---|---|
| \(\ce{(CH3)2NH + H2O ⇌ (CH3)2NH2+ + OH-}\) | 5.9 × 10−4 |
| \(\ce{CH3NH2 + H2O ⇌ CH3NH3+ + OH-}\) | 4.4 × 10−4 |
| \(\ce{(CH3)3N + H2O ⇌ (CH3)3NH+ + OH-}\) | 6.3 × 10−5 |
| \(\ce{NH3 + H2O ⇌ NH4+ + OH-}\) | 1.8 × 10−5 |
| \(\ce{C6H5NH2 + H2O ⇌ C6N5NH3+ + OH-}\) | 4.3 × 10−10 |
The following example shows that the concentration of products produced by the ionization of a weak base can be determined by the same series of steps used with a weak acid.
Find the concentration of hydroxide ion in a 0.25-M solution of trimethylamine, a weak base:
\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=6.3×10^{−5} \nonumber\]
Solution This problem requires that we calculate an equilibrium concentration by determining concentration changes as the ionization of a base goes to equilibrium. The solution is approached in the same way as that for the ionization of formic acid in Example \(\PageIndex{6}\). The reactants and products will be different and the numbers will be different, but the logic will be the same:

1. Determine x and equilibrium concentrations. The table shows the changes and concentrations:
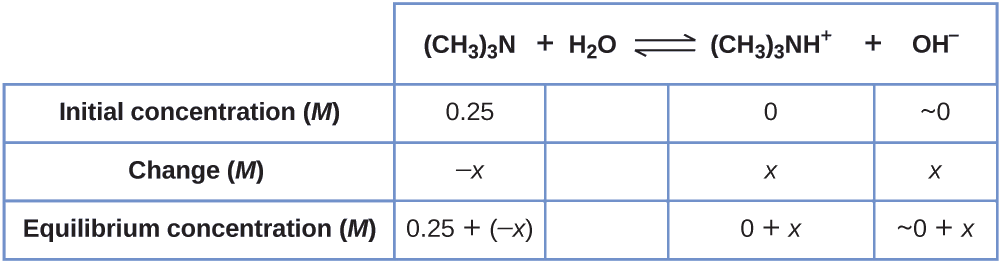
2. Solve for \(x\) and the equilibrium concentrations. At equilibrium:
\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}=\dfrac{(x)(x)}{0.25−x=}6.3×10^{−5} \nonumber\]
If we assume that x is small relative to 0.25, then we can replace (0.25 − x) in the preceding equation with 0.25. Solving the simplified equation gives:
\[x=4.0×10^{−3} \nonumber \]
This change is less than 5% of the initial concentration (0.25), so the assumption is justified.
Recall that, for this computation, \(x\) is equal to the equilibrium concentration of hydroxide ion in the solution (see earlier tabulation):
\[\begin{align*} (\ce{[OH- ]}=~0+x=x=4.0×10^{−3}\:M \\[4pt] &=4.0×10^{−3}\:M \end{align*}\]
Then calculate pOH as follows:
\[\ce{pOH}=−\log(4.3×10^{−3})=2.40 \nonumber\]
Using the relation introduced in the previous section of this chapter:
\[\mathrm{pH + pOH=p\mathit{K}_w=14.00}\nonumber \]
permits the computation of pH:
\[\mathrm{pH=14.00−pOH=14.00−2.37=11.60} \nonumber\]
Check the work. A check of our arithmetic shows that \(K_b = 6.3 \times 10^{−5}\).
Percent Ionization for Bases
As with acids, percent ionization can be measured for basic solutions, but will vary depending on the base ionization constant and the initial concentration of the solution.
\[\% \:\ce{ionization}=\ce{\dfrac{[BH+]_{eq}}{[B]_0}}×100\% \label{PercentIon} \]
Find the concentration of hydroxide ion in a 0.0325-M solution of ammonia, a weak base with a Kb of 1.76 × 10−5. Calculate the percent ionization of ammonia, the fraction ionized × 100, or \(\ce{\dfrac{[NH4+]}{[NH3]}}×100 \%\)
- Answer
-
\(7.56 × 10^{−4}\, M\), 2.33%
Ionization Constants for Conjugate Acid Base Pairs
The extent to which an acid, \(\ce{HA}\), donates protons to water molecules depends on the strength of the conjugate base, \(\ce{A^{−}}\), of the acid. If \(\ce{A^{−}}\) is a strong base, any protons that are donated to water molecules are recaptured by \(\ce{A^{−}}\). Thus there is relatively little \(\ce{A^{−}}\) and \(\ce{H3O+}\) in solution, and the acid, \(\ce{HA}\), is weak. If \(\ce{A^{−}}\) is a weak base, water binds the protons more strongly, and the solution contains primarily \(\ce{A^{−}}\) and \(\ce{H3O^{+}}\)—the acid is strong. Strong acids form very weak conjugate bases, and weak acids form stronger conjugate bases.
In an aqueous solution, the acid ionization constant for a particular acid (Ka) and the base ionization constant (Kb) for its conjugate base are related though Kw. Consider the ionization reactions for a conjugate acid-base pair, \(\ce{HA − A^{−}}\):
\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq)\]
with \(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\).
\[\ce{A-}(aq)+\ce{H2O}(l)⇌\ce{OH-}(aq)+\ce{HA}(aq)\]
with \(K_\ce{b}=\ce{\dfrac{[HA][OH]}{[A- ]}}\).
Adding these two chemical equations yields the equation for the autoionization for water:
\[\begin{align*} \cancel{\ce{HA}(aq)}+\ce{H2O}(l)+\cancel{\ce{A-}(aq)}+\ce{H2O}(l) &⇌ \ce{H3O+}(aq)+\cancel{\ce{A-}(aq)}+\ce{OH-}(aq)+\cancel{\ce{HA}(aq)} \\[4pt] \ce{2H2O}(l) &⇌\ce{H3O+}(aq)+\ce{OH-}(aq) \end{align*}\]
As shown in the previous chapter on equilibrium, the \(K\) expression for a chemical equation derived from adding two or more other equations is the mathematical product of the other equations’ \(K\) expressions. Multiplying the mass-action expressions together and cancelling common terms, we see that:
\[K_\ce{a}×K_\ce{b}=\ce{\dfrac{[H3O+][A- ]}{[HA]}×\dfrac{[HA][OH- ]}{[A- ]}}=\ce{[H3O+][OH- ]}=K_\ce{w}\]
For example, the acid ionization constant of acetic acid (CH3COOH) is 1.8 × 10−5, and the base ionization constant of its conjugate base, acetate ion (\(\ce{CH3COO-}\)), is 5.6 × 10−10. The product of these two constants is indeed equal to \(K_w\):
\[K_\ce{a}×K_\ce{b}=(1.8×10^{−5})×(5.6×10^{−10})=1.0×10^{−14}=K_\ce{w}\]
Use the \(K_b\) for the nitrite ion, \(\ce{NO2-}\), to calculate the \(K_a\) for its conjugate acid.
Solution
Kb for \(\ce{NO2-}\) is given in this section as 2.17 × 10−11. The conjugate acid of \(\ce{NO2-}\) is HNO2; Ka for HNO2 can be calculated using the relationship:
\[K_\ce{a}×K_\ce{b}=1.0×10^{−14}=K_\ce{w} \nonumber \]
Solving for Ka, we get:
\[\begin{align*} K_\ce{a} &=\dfrac{K_\ce{w}}{K_\ce{b}} \\[4pt] &=\dfrac{1.0×10^{−14}}{2.17×10^{−11}} \\[4pt] &=4.6×10^{−4} \end{align*}\]
This answer can be verified by finding the Ka for HNO2 in Table E1
We can determine the relative acid strengths of \(\ce{NH4+}\) and \(\ce{HCN}\) by comparing their ionization constants. The ionization constant of \(\ce{HCN}\) is given in Table E1 as 4.9 × 10−10. The ionization constant of \(\ce{NH4+}\) is not listed, but the ionization constant of its conjugate base, \(\ce{NH3}\), is listed as 1.8 × 10−5. Determine the ionization constant of \(\ce{NH4+}\), and decide which is the stronger acid, \(\ce{HCN}\) or \(\ce{NH4+}\).
- Answer
-
\(\ce{NH4+}\) is the slightly stronger acid (Ka for \(\ce{NH4+}\) = 5.6 × 10−10).
Summary
The strengths of Brønsted-Lowry acids and bases in aqueous solutions can be determined by their acid or base ionization constants. Stronger acids form weaker conjugate bases, and weaker acids form stronger conjugate bases. Thus strong acids are completely ionized in aqueous solution because their conjugate bases are weaker bases than water. Weak acids are only partially ionized because their conjugate bases are strong enough to compete successfully with water for possession of protons. Strong bases react with water to quantitatively form hydroxide ions. Weak bases give only small amounts of hydroxide ion. The strengths of the binary acids increase from left to right across a period of the periodic table (CH4 < NH3 < H2O < HF), and they increase down a group (HF < HCl < HBr < HI). The strengths of oxyacids that contain the same central element increase as the oxidation number of the element increases (H2SO3 < H2SO4). The strengths of oxyacids also increase as the electronegativity of the central element increases [H2SeO4 < H2SO4].
Key Equations
- \(K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\)
- \(K_a \times K_b = 1.0 \times 10^{−14} = K_w \,(\text{at room temperature})\)
- \(\textrm{Percent ionization}=\ce{\dfrac{[BH+]_{eq}}{[B]_0}}×100\)
Glossary
- base ionization constant (Kb)
- equilibrium constant for the ionization of a weak base
- leveling effect of water
- any acid stronger than \(\ce{H3O+}\), or any base stronger than OH− will react with water to form \(\ce{H3O+}\), or OH−, respectively; water acts as a base to make all strong acids appear equally strong, and it acts as an acid to make all strong bases appear equally strong
- percent ionization
- ratio of the concentration of the ionized acid/base to the initial acid/base concentration, times 100


