10.3: UV/Vis and IR Spectroscopy
- Page ID
- 220744
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Figure 10.1.9 we examined Nessler’s original method for matching the color of a sample to the color of a standard. Matching colors is a labor intensive process for the analyst and, not surprisingly, spectroscopic methods of analysis were slow to find favor. The 1930s and 1940s saw the introduction of photoelectric transducers for ultraviolet and visible radiation, and thermocouples for infrared radiation. As a result, modern instrumentation for absorption spectroscopy routinely became available in the 1940s—further progress has been rapid ever since.
Instrumentation
Frequently an analyst must select from among several instruments of different design, the one instrument best suited for a particular analysis. In this section we examine several different instruments for molecular absorption spectroscopy, with an emphasis on their advantages and limitations. Methods of sample introduction also are covered in this section.
Instrument Designs for Molecular UV/Vis Absorption
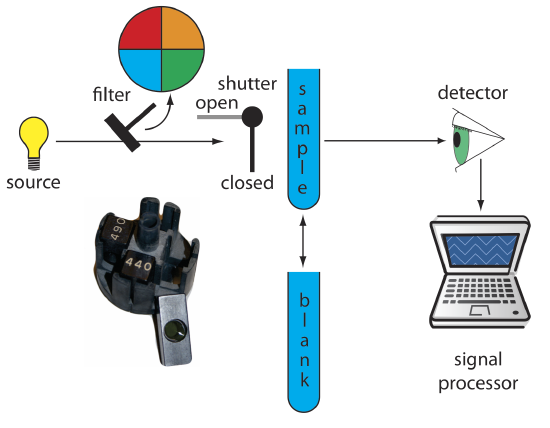
Filter Photometer. The simplest instrument for molecular UV/Vis absorption is a filter photometer (Figure \(\PageIndex{1}\)), which uses an absorption or interference filter to isolate a band of radiation. The filter is placed between the source and the sample to prevent the sample from decomposing when exposed to higher energy radiation. A filter photometer has a single optical path between the source and detector, and is called a single-beam instrument. The instrument is calibrated to 0% T while using a shutter to block the source radiation from the detector. After opening the shutter, the instrument is calibrated to 100% T using an appropriate blank. The blank is then replaced with the sample and its transmittance measured. Because the source’s incident power and the sensitivity of the detector vary with wavelength, the photometer is recalibrated whenever the filter is changed. Photometers have the advantage of being relatively inexpensive, rugged, and easy to maintain. Another advantage of a photometer is its portability, making it easy to take into the field. Disadvantages of a photometer include the inability to record an absorption spectrum and the source’s relatively large effective bandwidth, which limits the calibration curve’s linearity.
The percent transmittance varies between 0% and 100%. As we learned from Figure 10.2.7, we use a blank to determine P0, which corresponds to 100%T. Even in the absence of light the detector records a signal. Closing the shutter allows us to assign 0%T to this signal. Together, setting 0% T and 100%T calibrates the instrument. The amount of light that passes through a sample produces a signal that is greater than or equal to 0%T and smaller than or equal to 100%T.
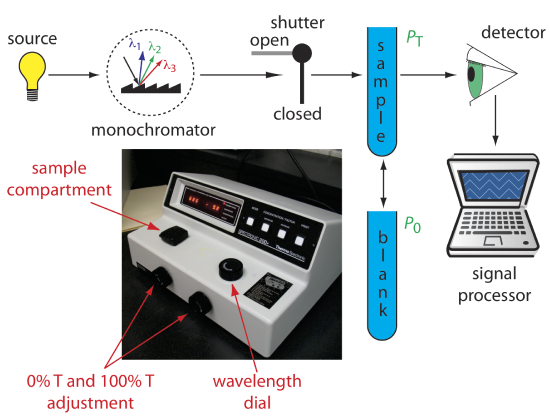
Single-Beam Spectrophotometer. An instrument that uses a monochromator for wavelength selection is called a spectrophotometer. The simplest spectrophotometer is a single-beam instrument equipped with a fixed-wavelength monochromator (Figure \(\PageIndex{2}\)). Single-beam spectrophotometers are calibrated and used in the same manner as a photometer. One example of a single-beam spectrophotometer is Thermo Scientific’s Spectronic 20D+, which is shown in the photographic insert to Figure \(\PageIndex{2}\). The Spectronic 20D+ has a wavelength range of 340–625 nm (950 nm when using a red-sensitive detector), and a fixed effective bandwidth of 20 nm. Battery-operated, hand-held single-beam spectrophotometers are available, which are easy to transport into the field. Other single-beam spectrophotometers also are available with effective bandwidths of 2–8 nm. Fixed wavelength single-beam spectrophotometers are not practical for recording spectra because manually adjusting the wavelength and recalibrating the spectrophotometer is awkward and time-consuming. The accuracy of a single-beam spectrophotometer is limited by the stability of its source and detector over time.
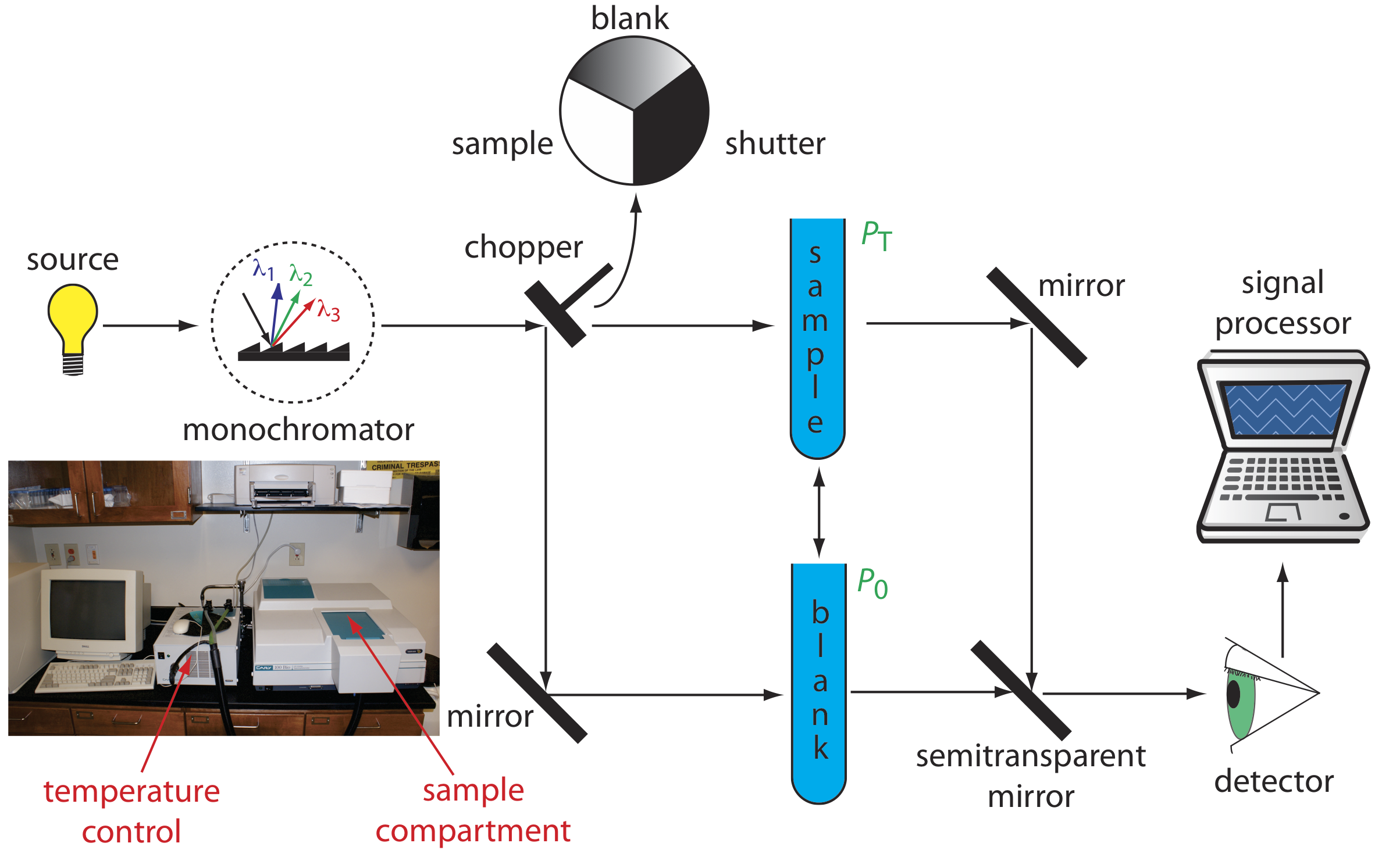
Double-Beam Spectrophotometer. The limitations of a fixed-wavelength, single-beam spectrophotometer is minimized by using a double-beam spectrophotometer (Figure \(\PageIndex{3}\)). A chopper controls the radiation’s path, alternating it between the sample, the blank, and a shutter. The signal processor uses the chopper’s speed of rotation to resolve the signal that reaches the detector into the transmission of the blank, P0, and the sample, PT. By including an opaque surface as a shutter, it also is possible to continuously adjust 0%T. The effective bandwidth of a double-beam spectrophotometer is controlled by adjusting the monochromator’s entrance and exit slits. Effective bandwidths of 0.2–3.0 nm are common. A scanning monochromator allows for the automated recording of spectra. Double-beam instruments are more versatile than single-beam instruments, being useful for both quantitative and qualitative analyses, but also are more expensive and not particularly portable.
Diode Array Spectrometer. An instrument with a single detector can monitor only one wavelength at a time. If we replace a single photomultiplier with an array of photodiodes, we can use the resulting detector to record a full spectrum in as little as 0.1 s. In a diode array spectrometer the source radiation passes through the sample and is dispersed by a grating (Figure \(\PageIndex{4}\)). The photodiode array detector is situated at the grating’s focal plane, with each diode recording the radiant power over a narrow range of wavelengths. Because we replace a full monochromator with just a grating, a diode array spectrometer is small and compact.
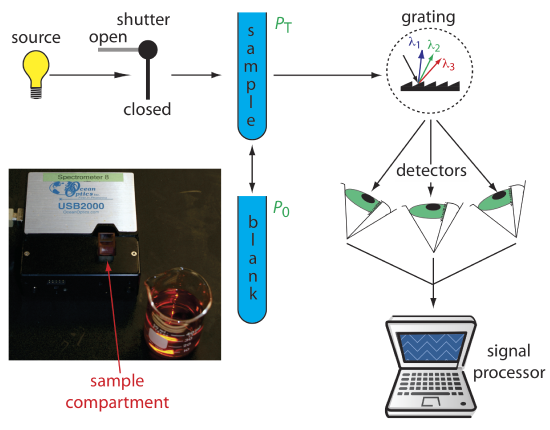
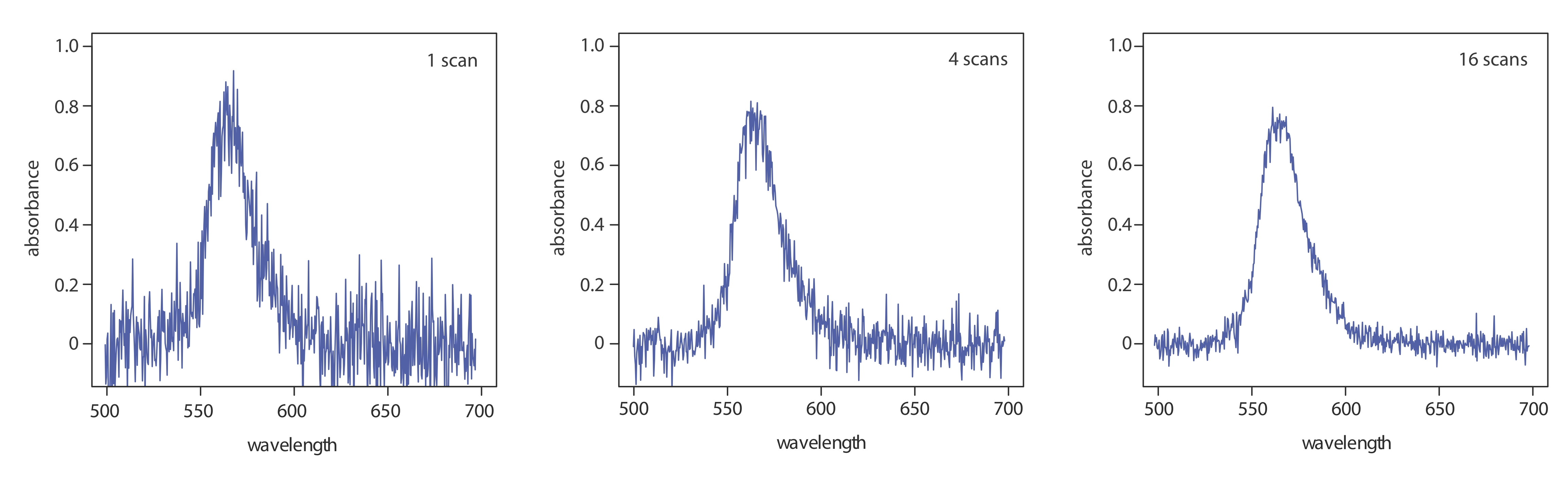
One advantage of a diode array spectrometer is the speed of data acquisition, which allows us to collect multiple spectra for a single sample. Individual spectra are added and averaged to obtain the final spectrum. This signal averaging improves a spectrum’s signal-to-noise ratio. If we add together n spectra, the sum of the signal at any point, x, increases as nSx, where Sx is the signal. The noise at any point, Nx, is a random event, which increases as \(\sqrt{n} N_x\) when we add together n spectra. The signal-to-noise ratio after n scans, (S/N)n is
\[\left(\frac{S}{N}\right)_{n}=\frac{n S_{x}}{\sqrt{n} N_{x}}=\sqrt{n} \frac{S_{x}}{N_{x}} \nonumber\]
where Sx/Nx is the signal-to-noise ratio for a single scan. The impact of signal averaging is shown in Figure \(\PageIndex{5}\). The first spectrum shows the signal after one scan, which consists of a single, noisy peak. Signal averaging using 4 scans and 16 scans decreases the noise and improves the signal-to-noise ratio. One disadvantage of a photodiode array is that the effective bandwidth per diode is roughly an order of magnitude larger than that for a high quality monochromator.
For more details on signals and noise, see Introduction to Signals and Noise by Steven Petrovic, an on-line resource that is part of the Analytical Sciences Digital Library.
Sample Cells. The sample compartment provides a light-tight environment that limits stray radiation. Samples normally are in a liquid or solution state, and are placed in cells constructed with UV/Vis transparent materials, such as quartz, glass, and plastic (Figure \(\PageIndex{6}\)). A quartz or fused-silica cell is required when working at a wavelength <300 nm where other materials show a significant absorption. The most common pathlength is 1 cm (10 mm), although cells with shorter (as little as 0.1 cm) and longer pathlengths (up to 10 cm) are available. Longer pathlength cells are useful when analyzing a very dilute solution or for gas samples. The highest quality cells allow the radiation to strike a flat surface at a 90o angle, minimizing the loss of radiation to reflection. A test tube often is used as a sample cell with simple, single-beam instruments, although differences in the cell’s pathlength and optical properties add an additional source of error to the analysis.

If we need to monitor an analyte’s concentration over time, it may not be possible to remove samples for analysis. This often is the case, for example, when monitoring an industrial production line or waste line, when monitoring a patient’s blood, or when monitoring an environmental system, such as stream. With a fiber-optic probe we can analyze samples in situ. An example of a remote sensing fiber-optic probe is shown in Figure \(\PageIndex{7}\). The probe consists of two bundles of fiber-optic cable. One bundle transmits radiation from the source to the probe’s tip, which is designed to allow the sample to flow through the sample cell. Radiation from the source passes through the solution and is reflected back by a mirror. The second bundle of fiber-optic cable transmits the nonabsorbed radiation to the wavelength selector. Another design replaces the flow cell shown in Figure \(\PageIndex{7}\) with a membrane that contains a reagent that reacts with the analyte. When the analyte diffuses into the membrane it reacts with the reagent, producing a product that absorbs UV or visible radiation. The nonabsorbed radiation from the source is reflected or scattered back to the detector. Fiber optic probes that show chemical selectivity are called optrodes [(a) Seitz, W. R. Anal. Chem. 1984, 56, 16A–34A; (b) Angel, S. M. Spectroscopy 1987, 2(2), 38–48].

Instrument Designs for Infrared Adsorption
Filter Photometer. The simplest instrument for IR absorption spectroscopy is a filter photometer similar to that shown in Figure \(\PageIndex{1}\) for UV/Vis absorption. These instruments have the advantage of portability and typically are used as dedicated analyzers for gases such as HCN and CO.
Double-beam spectrophotometer. Infrared instruments using a monochromator for wavelength selection use double-beam optics similar to that shown in Figure \(\PageIndex{3}\). Double-beam optics are preferred over single-beam optics because the sources and detectors for infrared radiation are less stable than those for UV/Vis radiation. In addition, it is easier to correct for the absorption of infrared radiation by atmospheric CO2 and H2O vapor when using double-beam optics. Resolutions of 1–3 cm–1 are typical for most instruments.
Fourier transform spectrometer. In a Fourier transform infrared spectrometer, or FT–IR, the monochromator is replaced with an interferometer (Figure 10.1.13). Because an FT-IR includes only a single optical path, it is necessary to collect a separate spectrum to compensate for the absorbance of atmospheric CO2 and H2O vapor. This is done by collecting a background spectrum without the sample and storing the result in the instrument’s computer memory. The background spectrum is removed from the sample’s spectrum by taking the ratio the two signals. In comparison to other instrument designs, an FT–IR provides for rapid data acquisition, which allows for an enhancement in signal-to-noise ratio through signal-averaging.
Sample Cells. Infrared spectroscopy routinely is used to analyze gas, liquid, and solid samples. Sample cells are made from materials, such as NaCl and KBr, that are transparent to infrared radiation. Gases are analyzed using a cell with a pathlength of approximately 10 cm. Longer pathlengths are obtained by using mirrors to pass the beam of radiation through the sample several times.
A liquid sample may be analyzed using a variety of different sample cells (Figure \(\PageIndex{8}\)). For non-volatile liquids a suitable sample is prepared by placing a drop of the liquid between two NaCl plates, forming a thin film that typically is less than 0.01 mm thick. Volatile liquids are placed in a sealed cell to prevent their evaporation.

The analysis of solution samples is limited by the solvent’s IR absorbing properties, with CCl4, CS2, and CHCl3 being the most common solvents. Solutions are placed in cells that contain two NaCl windows separated by a Teflon spacer. By changing the Teflon spacer, pathlengths from 0.015–1.0 mm are obtained.
Transparent solid samples are analyzed by placing them directly in the IR beam. Most solid samples, however, are opaque, and are first dispersed in a more transparent medium before recording the IR spectrum. If a suitable solvent is available, then the solid is analyzed by preparing a solution and analyzing as described above. When a suitable solvent is not available, solid samples are analyzed by preparing a mull of the finely powdered sample with a suitable oil. Alternatively, the powdered sample is mixed with KBr and pressed into an optically transparent pellet.
The analysis of an aqueous sample is complicated by the solubility of the NaCl cell window in water. One approach to obtaining an infrared spectrum of an aqueous solution is to use attenuated total reflectance instead of transmission. Figure \(\PageIndex{9}\) shows a diagram of a typical attenuated total reflectance (ATR) FT–IR instrument. The ATR cell consists of a high refractive index material, such as ZnSe or diamond, sandwiched between a low refractive index substrate and a lower refractive index sample. Radiation from the source enters the ATR crystal where it undergoes a series of internal reflections before exiting the crystal. During each reflection the radiation penetrates into the sample to a depth of a few microns, which results in a selective attenuation of the radiation at those wavelengths where the sample absorbs. ATR spectra are similar, but not identical, to those obtained by measuring the transmission of radiation.
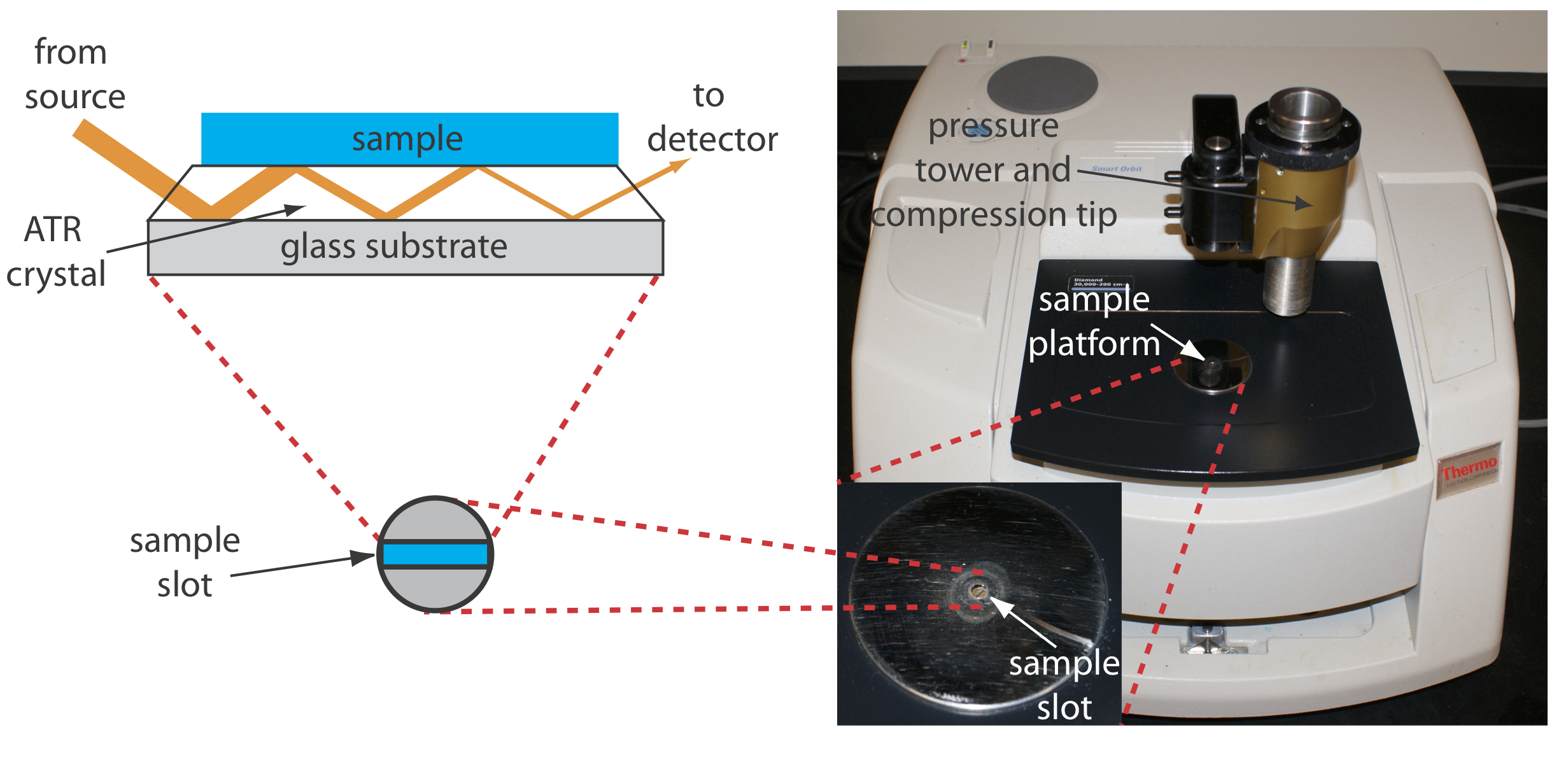
Solid samples also can be analyzed using an ATR sample cell. After placing the solid in the sample slot, a compression tip ensures that it is in contact with the ATR crystal. Examples of solids analyzed by ATR include polymers, fibers, fabrics, powders, and biological tissue samples. Another reflectance method is diffuse reflectance, in which radiation is reflected from a rough surface, such as a powder. Powdered samples are mixed with a non-absorbing material, such as powdered KBr, and the reflected light is collected and analyzed. As with ATR, the resulting spectrum is similar to that obtained by conventional transmission methods. Further details about these, and other methods for preparing solids for infrared analysis can be found in this chapter’s additional resources.
Quantitative Applications
The determination of an analyte’s concentration based on its absorption of ultraviolet or visible radiation is one of the most frequently encountered quantitative analytical methods. One reason for its popularity is that many organic and inorganic compounds have strong absorption bands in the UV/Vis region of the electromagnetic spectrum. In addition, if an analyte does not absorb UV/Vis radiation—or if its absorbance is too weak—we often can react it with another species that is strongly absorbing. For example, a dilute solution of Fe2+ does not absorb visible light. Reacting Fe2+ with o-phenanthroline, however, forms an orange–red complex of \(\text{Fe(phen)}_3^{2+}\) that has a strong, broad absorbance band near 500 nm. An additional advantage to UV/Vis absorption is that in most cases it is relatively easy to adjust experimental and instrumental conditions so that Beer’s law is obeyed.
A quantitative analysis based on the absorption of infrared radiation, although important, is encountered less frequently than with UV/Vis absorption. One reason is the greater tendency for instrumental deviations from Beer’s law when using infrared radiation. Because an infrared absorption band is relatively narrow, any deviation due to the lack of monochromatic radiation is more pronounced. In addition, infrared sources are less intense than UV/Vis sources, which makes stray radiation more of a problem. Differences between the pathlengths for samples and for standards when using thin liquid films or KBr pellets are a problem, although an internal standard can correct for any difference in pathlength. Finally, establishing a 100%T (A = 0) baseline often is difficult because the optical properties of NaCl sample cells may change significantly with wavelength due to contamination and degradation. We can minimize this problem by measuring absorbance relative to a baseline established for the absorption band. Figure \(\PageIndex{10}\) shows how this is accomplished.
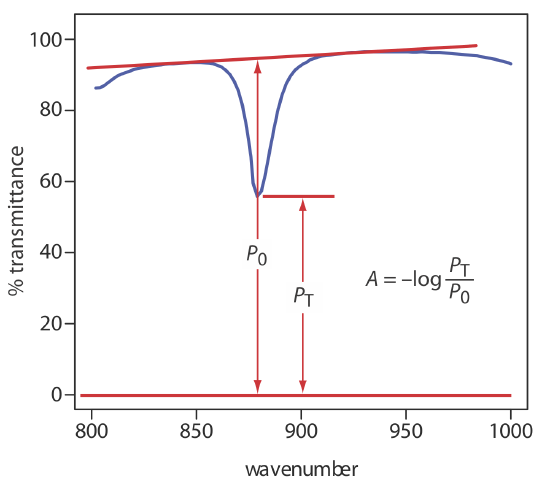
Another approach is to use a cell with a fixed pathlength, such as that shown in Figure \(\PageIndex{8}\)b.
Environmental Applications
The analysis of waters and wastewaters often relies on the absorption of ultraviolet and visible radiation. Many of these methods are outlined in Table \(\PageIndex{1}\). Several of these methods are described here in more detail.
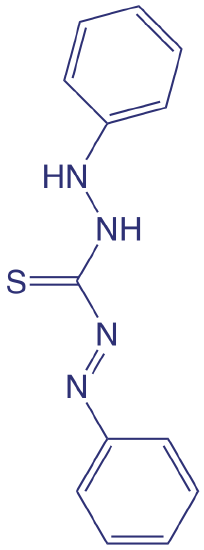
Although the quantitative analysis of metals in waters and wastewaters is accomplished primarily by atomic absorption or atomic emission spectroscopy, many metals also can be analyzed following the formation of a colored metal–ligand complex. One advantage to these spectroscopic methods is that they easily are adapted to the analysis of samples in the field using a filter photometer. One ligand used for the analysis of several metals is diphenylthiocarbazone, also known as dithizone. Dithizone is not soluble in water, but when a solution of dithizone in CHCl3 is shaken with an aqueous solution that contains an appropriate metal ion, a colored metal–dithizonate complex forms that is soluble in CHCl3. The selectivity of dithizone is controlled by adjusting the sample’s pH. For example, Cd2+ is extracted from solutions made strongly basic with NaOH, Pb2+ from solutions made basic with an NH3/ NH4+ buffer, and Hg2+ from solutions that are slightly acidic.
The structure of dithizone is shown below. See Chapter 7 for a discussion of extracting metal ions using dithizone.
When chlorine is added to water the portion available for disinfection is called the chlorine residual. There are two forms of chlorine residual. The free chlorine residual includes Cl2, HOCl, and OCl–. The combined chlorine residual, which forms from the reaction of NH3 with HOCl, consists of monochloramine, NH2Cl, dichloramine, NHCl2, and trichloramine, NCl3. Because the free chlorine residual is more efficient as a disinfectant, there is an interest in methods that can distinguish between the total chlorine residual’s different forms. One such method is the leuco crystal violet method. The free residual chlorine is determined by adding leuco crystal violet to the sample, which instantaneously oxidizes to give a blue-colored compound that is monitored at 592 nm. Completing the analysis in less than five minutes prevents a possible interference from the combined chlorine residual. The total chlorine residual (free + combined) is determined by reacting a separate sample with iodide, which reacts with both chlorine residuals to form HOI. When the reaction is complete, leuco crystal violet is added and oxidized by HOI, giving the same blue-colored product. The combined chlorine residual is determined by difference.
In Chapter 9 we explored how the total chlorine residual can be determined by a redox titration; see Representative Method 9.4.1 for further details. The method described here allows us to divide the total chlorine residual into its component parts.
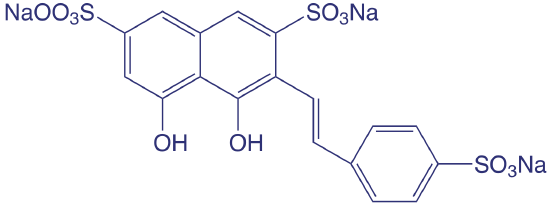
The concentration of fluoride in drinking water is determined indirectly by its ability to form a complex with zirconium. In the presence of the dye SPADNS, a solution of zirconium forms a red colored compound, called a lake, that absorbs at 570 nm. When fluoride is added, the formation of the stable \(\text{ZrF}_6^{2-}\) complex causes a portion of the lake to dissociate, decreasing the absorbance. A plot of absorbance versus the concentration of fluoride, therefore, has a negative slope.
SPADNS, the structure of which is shown below, is an abbreviation for the sodium salt of 2-(4-sulfophenylazo)-1,8-dihydroxy-3,6-napthalenedisulfonic acid, which is a mouthful to say.
Spectroscopic methods also are used to determine organic constituents in water. For example, the combined concentrations of phenol and ortho- and meta-substituted phenols are determined by using steam distillation to separate the phenols from nonvolatile impurities. The distillate reacts with 4-aminoantipyrine at pH 7.9 ± 0.1 in the presence of K3Fe(CN)6 to a yellow colored antipyrine dye. After extracting the dye into CHCl3, its absorbance is monitored at 460 nm. A calibration curve is prepared using only the unsubstituted phenol, C6H5OH. Because the molar absorptivity of substituted phenols generally are less than that for phenol, the reported concentration represents the minimum concentration of phenolic compounds.
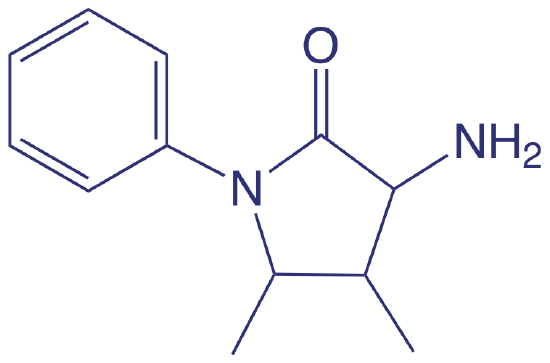
4-aminoantipyrene
Molecular absorption also is used for the analysis of environmentally significant airborne pollutants. In many cases the analysis is carried out by collecting the sample in water, converting the analyte to an aqueous form that can be analyzed by methods such as those described in Table \(\PageIndex{1}\). For example, the concentration of NO2 is determined by oxidizing NO2 to \(\text{NO}_3^-\). The concentration of \(\text{NO}_3^-\) is then determined by first reducing it to \(\text{NO}_2^-\) with Cd, and then reacting \(\text{NO}_2^-\) with sulfanilamide and N-(1-naphthyl)-ethylenediamine to form a red azo dye. Another important application is the analysis for SO2, which is determined by collecting the sample in an aqueous solution of \(\text{HgCl}_4^{2-}\) where it reacts to form \(\text{Hg(SO}_3)_2^{2-}\). Addition of p-rosaniline and formaldehyde produces a purple complex that is monitored at 569 nm. Infrared absorption is useful for the analysis of organic vapors, including HCN, SO2, nitrobenzene, methyl mercaptan, and vinyl chloride. Frequently, these analyses are accomplished using portable, dedicated infrared photometers.
Clinical Applications
The analysis of clinical samples often is complicated by the complexity of the sample’s matrix, which may contribute a significant background absorption at the desired wavelength. The determination of serum barbiturates provides one example of how this problem is overcome. The barbiturates are first extracted from a sample of serum with CHCl3 and then extracted from the CHCl3 into 0.45 M NaOH (pH ≈ 13). The absorbance of the aqueous extract is measured at 260 nm, and includes contributions from the barbiturates as well as other components extracted from the serum sample. The pH of the sample is then lowered to approximately 10 by adding NH4Cl and the absorbance remeasured. Because the barbiturates do not absorb at this pH, we can use the absorbance at pH 10, ApH 10, to correct the absor-ance at pH 13, ApH 13
\[A_\text{barb} = A_\text{pH 13} - \frac {V_\text{samp} + V_{\text{NH}_4\text{Cl}}} {V_\text{samp}} \times A_\text{pH 10} \nonumber\]
where Abarb is the absorbance due to the serum barbiturates and Vsamp and \(V_{\text{NH}_4\text{Cl}}\) are the volumes of sample and NH4Cl, respectively. Table \(\PageIndex{2}\) provides a summary of several other methods for analyzing clinical samples.
Industrial Applications
UV/Vis molecular absorption is used for the analysis of a diverse array of industrial samples including pharmaceuticals, food, paint, glass, and metals. In many cases the methods are similar to those described in Table \(\PageIndex{1}\) and in Table \(\PageIndex{2}\). For example, the amount of iron in food is determined by bringing the iron into solution and analyzing using the o-phenanthroline method listed in Table \(\PageIndex{1}\).
Many pharmaceutical compounds contain chromophores that make them suitable for analysis by UV/Vis absorption. Products analyzed in this fashion include antibiotics, hormones, vitamins, and analgesics. One example of the use of UV absorption is in determining the purity of aspirin tablets, for which the active ingredient is acetylsalicylic acid. Salicylic acid, which is produced by the hydrolysis of acetylsalicylic acid, is an undesirable impurity in aspirin tablets, and should not be present at more than 0.01% w/w. Samples are screened for unacceptable levels of salicylic acid by monitoring the absorbance at a wavelength of 312 nm. Acetylsalicylic acid absorbs at 280 nm, but absorbs poorly at 312 nm. Conditions for preparing the sample are chosen such that an absorbance of greater than 0.02 signifies an unacceptable level of salicylic acid.
Forensic Applications
UV/Vis molecular absorption routinely is used for the analysis of narcotics and for drug testing. One interesting forensic application is the determination of blood alcohol using the Breathalyzer test. In this test a 52.5-mL breath sample is bubbled through an acidified solution of K2Cr2O7, which oxidizes ethanol to acetic acid. The concentration of ethanol in the breath sample is determined by a decrease in the absorbance at 440 nm where the dichromate ion absorbs. A blood alcohol content of 0.10%, which is above the legal limit, corresponds to 0.025 mg of ethanol in the breath sample.
Developing a Quantitative Method for a Single Component
To develop a quantitative analytical method, the conditions under which Beer’s law is obeyed must be established. First, the most appropriate wavelength for the analysis is determined from an absorption spectrum. In most cases the best wavelength corresponds to an absorption maximum because it provides greater sensitivity and is less susceptible to instrumental limitations. Second, if the instrument has adjustable slits, then an appropriate slit width is chosen. The absorption spectrum also aids in selecting a slit width by choosing a width that is narrow enough to avoid instrumental limita- tions to Beer’s law, but wide enough to increase the throughput of source radiation. Finally, a calibration curve is constructed to determine the range of concentrations for which Beer’s law is valid. Additional considerations that are important in any quantitative method are the effect of potential interferents and establishing an appropriate blank.
Representative Method 10.3.1: Determination of Iron in Water and Wastewater
The best way to appreciate the theoretical and the practical details discussed in this section is to carefully examine a typical analytical method. Although each method is unique, the following description of the determination of iron in water and waste- water provides an instructive example of a typical procedure. The description here is based on Method 3500-Fe B as published in Standard Methods for the Examination of Water and Wastewater, 20th Ed., American Public Health Association: Washington, D. C., 1998.
Description of Method
Iron in the +2 oxidation state reacts with o-phenanthroline to form the orange-red \(\text{Fe(phen)}_3^{2+}\) complex. The intensity of the complex’s color is independent of the solution’s acidity between a pH of 3 and 9. Because the complex forms more rapidly at lower pH levels, the reaction usually is carried out within a pH range of 3.0–3.5. Any iron present in the +3 oxidation state is reduced with hydroxylamine before adding o-phenanthroline. The most important interferents are strong oxidizing agents, polyphosphates, and metal ions such as Cu2+, Zn2+, Ni2+, and Cd2+. An interference from oxidizing agents is minimized by adding an excess of hydroxylamine, and an interference from polyphosphate is minimized by boiling the sample in the presence of acid. The absorbance of samples and standards are measured at a wavelength of 510 nm using a 1-cm cell (longer pathlength cells also may be used). Beer’s law is obeyed for concentrations of within the range of 0.2–4.0 mg Fe/L.
Procedure
For a sample that contains less than 2 mg Fe/L, directly transfer a 50-mL portion to a 125-mL Erlenmeyer flask. Samples that contain more than 2 mg Fe/L are diluted before acquiring the 50-mL portion. Add 2 mL of concentrated HCl and 1 mL of hydroxylamine to the sample. Bring the solution to a boil and continue boiling until the solution’s volume is reduced to between 15 and 20 mL. After cooling to room temperature, transfer the solution to a 50-mL volumetric flask, add 10 mL of an ammonium acetate buffer, 2 mL of a 1000 ppm solution of o-phenanthroline, and dilute to volume. Allow 10–15 minutes for color development before measuring the absorbance, using distilled water to set 100% T. Calibration standards, including a blank, are prepared by the same procedure using a stock solution that contains a known concentration of Fe2+.
Questions
1. Explain why strong oxidizing agents are interferents and why an excess of hydroxylamine prevents the interference.
A strong oxidizing agent will oxidize some Fe2+ to Fe3+. Because \(\text{Fe(phen)}_3^{3+}\) does not absorb as strongly as \(\text{Fe(phen)}_3^{2+}\), the absorbance is smaller than expected, which produces a negative determinate error. The excess hydroxylamine reacts with the oxidizing agents, removing them from the solution.
2. The color of the complex is stable between pH levels of 3 and 9. What are some possible complications at more acidic or at more basic pH’s?
Because o-phenanthroline is a weak base, its conditional formation constant for \(\text{Fe(phen)}_3^{2+}\) becomes smaller at more acidic pH levels, where o-phenanthroline is present in its protonated form. The result is a decrease in absorbance and a less sensitive analytical method. When the pH is greater than 9, competition between OH– and o-phenanthroline for Fe2+ also decreases the absorbance. In addition, if the pH is sufficiently basic there is a risk that the iron will precipitate as Fe(OH)2.
3. Cadmium is an interferent because it forms a precipitate with o-phenanthroline. What effect does the formation of precipitate have on the determination of iron?
Because o-phenanthroline is present in large excess (2000 μg of o-phenanthroline for 100 μg of Fe2+), it is not likely that the interference is due to an insufficient amount of o-phenanthroline being available to react with the Fe2+. The presence of a precipitate in the sample cell results in the scattering of radiation, which causes an apparent increase in absorbance. Because the measured absorbance increases, the reported concentration is too high. Although scattering is a problem here, it can serve as the basis of a useful analytical method. See Chapter 10.8 for further details.
4. Even high quality ammonium acetate contains a significant amount of iron. Why is this source of iron not a problem?
Because all samples and standards are prepared using the same volume of ammonium acetate buffer, the contribution of this source of iron is accounted for by the calibration curve’s reagent blank.
Quantitative Analysis for a Single Sample
To determine the concentration of an analyte we measure its absorbance and apply Beer’s law using any of the standardization methods described in Chapter 5. The most common methods are a normal calibration curve using external standards and the method of standard additions. A single point standardization also is possible, although we must first verify that Beer’s law holds for the concentration of analyte in the samples and the standard.
The determination of iron in an industrial waste stream is carried out by the o-phenanthroline described in Representative Method 10.3.1. Using the data in the following table, determine the mg Fe/L in the waste stream.
| mg Fe/L | absorbance |
|---|---|
| 0.00 | 0.000 |
| 1.00 | 0.183 |
| 2.00 | 0.364 |
| 3.00 | 0.546 |
| 4.00 | 0.727 |
| sample | 0.269 |
Solution
Linear regression of absorbance versus the concentration of Fe in the standards gives the calibration curve and calibration equation shown here
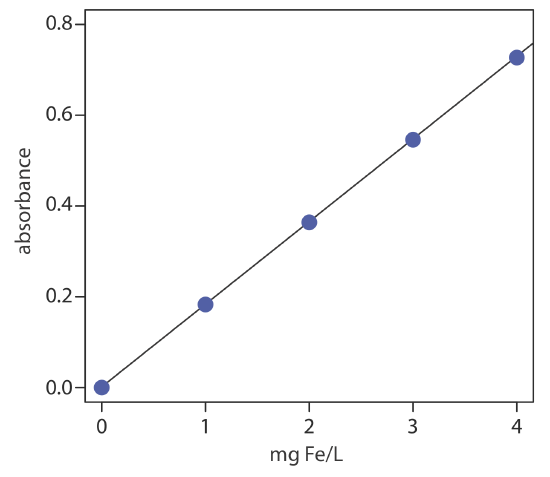
\[A=0.0006+\left(0.1817 \ \mathrm{mg}^{-1} \mathrm{L}\right) \times(\mathrm{mg} \mathrm{Fe} / \mathrm{L}) \nonumber\]
Substituting the sample’s absorbance into the calibration equation gives the concentration of Fe in the waste stream as 1.48 mg Fe/L
The concentration of Cu2+ in a sample is determined by reacting it with the ligand cuprizone and measuring its absorbance at 606 nm in a 1.00-cm cell. When a 5.00-mL sample is treated with cuprizone and diluted to 10.00 mL, the resulting solution has an absorbance of 0.118. A second 5.00-mL sample is mixed with 1.00 mL of a 20.00 mg/L standard of Cu2+, treated with cuprizone and diluted to 10.00 mL, giving an absorbance of 0.162. Report the mg Cu2+/L in the sample.
- Answer
-
For this standard addition we write equations that relate absorbance to the concentration of Cu2+ in the sample before the standard addition
\[0.118=\varepsilon b \left[ C_{\mathrm{Cu}} \times \frac{5.00 \text{ mL}}{10.00 \text{ mL}}\right] \nonumber\]
and after the standard addition
\[0.162=\varepsilon b\left(C_{\mathrm{Cu}} \times \frac{5.00 \text{ mL}}{10.00 \text{ mL}}+\frac{20.00 \ \mathrm{mg} \ \mathrm{Cu}}{\mathrm{L}} \times \frac{1.00 \ \mathrm{mL}}{10.00 \ \mathrm{mL}}\right) \nonumber\]
in each case accounting for the dilution of the original sample and for the standard. The value of \(\varepsilon b\) is the same in both equation. Solving each equation for \(\varepsilon b\) and equating
\[\frac{0.162}{C_{\mathrm{Cu}} \times \frac{5.00 \text{ mL}}{10.00 \text{ mL}}+\frac{20.00 \ \mathrm{mg} \ \mathrm{Cu}}{\mathrm{L}} \times \frac{1.00 \ \mathrm{mL}}{10.00 \ \mathrm{mL}}}=\frac{0.118}{C_{\mathrm{Cu}} \times \frac{5.00 \text{ mL}}{10.00 \text{ mL}}} \nonumber\]
leaves us with an equation in which CCu is the only variable. Solving for CCu gives its value as
\[\frac{0.162}{0.500 \times C_{\mathrm{Cu}}+2.00 \ \mathrm{mg} \ \mathrm{Cu} / \mathrm{L}}=\frac{0.118}{0.500 \times C_{\mathrm{Cu}}} \nonumber\]
\[0.0810 \times C_{\mathrm{Cu}}=0.0590 \times C_{\mathrm{Ca}}+0.236 \ \mathrm{mg} \ \mathrm{Cu} / \mathrm{L} \nonumber\]
\[0.0220 \times C_{\mathrm{Cu}}=0.236 \ \mathrm{mg} \ \mathrm{Cu} / \mathrm{L} \nonumber\]
\[C_{\mathrm{Cu}}=10.7 \ \mathrm{mg} \ \mathrm{Cu} / \mathrm{L} \nonumber\]
Quantitative Analysis of Mixtures
Suppose we need to determine the concentration of two analytes, X and Y, in a sample. If each analyte has a wavelength where the other analyte does not absorb, then we can proceed using the approach in Example \(\PageIndex{5}\). Unfortunately, UV/Vis absorption bands are so broad that frequently it is not possible to find suitable wavelengths. Because Beer’s law is additive the mixture’s absorbance, Amix, is
\[\left(A_{m i x}\right)_{\lambda_{1}}=\left(\varepsilon_{x}\right)_{\lambda_{1}} b C_{X}+\left(\varepsilon_{Y}\right)_{\lambda_{1}} b C_{Y} \label{10.1}\]
where \(\lambda_1\) is the wavelength at which we measure the absorbance. Because Equation \ref{10.1} includes terms for the concentration of both X and Y, the absorbance at one wavelength does not provide enough information to determine either CX or CY. If we measure the absorbance at a second wavelength
\[\left(A_{m i x}\right)_{\lambda_{2}}=\left(\varepsilon_{x}\right)_{\lambda_{2}} b C_{X}+\left(\varepsilon_{Y}\right)_{\lambda_{2}} b C_{Y} \label{10.2}\]
then we can determine CX and CY by solving simultaneously Equation \ref{10.1} and Equation \ref{10.2}. Of course, we also must determine the value for \(\varepsilon_X\) and \(\varepsilon_Y\) at each wavelength. For a mixture of n components, we must measure the absorbance at n different wavelengths.
The concentrations of Fe3+ and Cu2+ in a mixture are determined following their reaction with hexacyanoruthenate (II), \(\text{Ru(CN)}_6^{4-}\), which forms a purple-blue complex with Fe3+ (\(\lambda_\text{max}\) = 550 nm) and a pale-green complex with Cu2+ (\(\lambda_\text{max}\) = 396 nm) [DiTusa, M. R.; Schlit, A. A. J. Chem. Educ. 1985, 62, 541–542]. The molar absorptivities (M–1 cm–1) for the metal complexes at the two wavelengths are summarized in the following table.
| analyte | \(\varepsilon_{550}\) | \(\varepsilon_{396}\) |
|---|---|---|
| Fe3+ | 9970 | 84 |
| Cu2+ | 34 | 856 |
When a sample that contains Fe3+ and Cu2+ is analyzed in a cell with a pathlength of 1.00 cm, the absorbance at 550 nm is 0.183 and the absorbance at 396 nm is 0.109. What are the molar concentrations of Fe3+ and Cu2+ in the sample?
Solution
Substituting known values into Equation \ref{10.1} and Equation \ref{10.2} gives
\[\begin{aligned} A_{550} &=0.183=9970 C_{\mathrm{Fe}}+34 C_{\mathrm{Cu}} \\ A_{396} &=0.109=84 C_{\mathrm{Fe}}+856 C_{\mathrm{Cu}} \end{aligned} \nonumber\]
To determine CFe and CCu we solve the first equation for CCu
\[C_{\mathrm{Cu}}=\frac{0.183-9970 C_{\mathrm{Fe}}}{34} \nonumber\]
and substitute the result into the second equation.
\[\begin{aligned} 0.109 &=84 C_{\mathrm{Fe}}+856 \times \frac{0.183-9970 C_{\mathrm{Fe}}}{34} \\ &=4.607-\left(2.51 \times 10^{5}\right) C_{\mathrm{Fe}} \end{aligned} \nonumber\]
Solving for CFe gives the concentration of Fe3+ as \(1.8 \times 10^{-5}\) M. Substituting this concentration back into the equation for the mixture’s absorbance at 396 nm gives the concentration of Cu2+ as \(1.3 \times 10^{-4}\) M.
Another approach to solving Example \(\PageIndex{2}\) is to multiply the first equation by 856/34 giving
\[4.607=251009 C_{\mathrm{Fe}}+856 C_\mathrm{Cu} \nonumber\]
Subtracting the second equation from this equation
\[\begin{aligned} 4.607 &=251009 C_{\mathrm{Fe}}+856 C_{\mathrm{Cu}} \\-0.109 &=84 C_{\mathrm{Fe}}+856 C_{\mathrm{Cu}} \end{aligned} \nonumber\]
gives
\[4.498=250925 C_{\mathrm{Fe}} \nonumber\]
and we find that CFe is \(1.8 \times 10^{-5}\). Having determined CFe we can substitute back into one of the other equations to solve for CCu, which is \(1.3 \times 10^{-5}\).
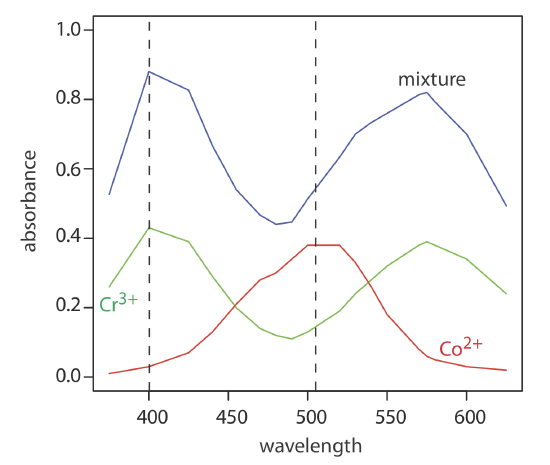
The absorbance spectra for Cr3+ and Co2+ overlap significantly. To determine the concentration of these analytes in a mixture, its absorbance is measured at 400 nm and at 505 nm, yielding values of 0.336 and 0.187, respectively. The individual molar absorptivities (M–1 cm–1) for Cr3+ are 15.2 at 400 nm and 0.533 at 505 nm; the values for Co2+ are 5.60 at 400 nm and 5.07 at 505 nm.
- Answer
-
Substituting into Equation \ref{10.1} and Equation \ref{10.2} gives
\[A_{400} = 0.336 = 15.2C_\text{Cr} + 5.60C_\text{Co} \nonumber\]
\[A_{400} = 0187 = 0.533C_\text{Cr} + 5.07C_\text{Co} \nonumber\]
To determine CCr and CCo we solve the first equation for CCo
\[C_{\mathrm{Co}}=\frac{0.336-15.2 \mathrm{C}_{\mathrm{Co}}}{5.60} \nonumber\]
and substitute the result into the second equation.
\[0.187=0.533 C_{\mathrm{Cr}}+5.07 \times \frac{0.336-15.2 C_{\mathrm{Co}}}{5.60} \nonumber\]
\[0.187=0.3042-13.23 C_{\mathrm{Cr}} \nonumber\]
Solving for CCr gives the concentration of Cr3+ as \(8.86 \times 10^{-3}\) M. Substituting this concentration back into the equation for the mixture’s absorbance at 400 nm gives the concentration of Co2+ as \(3.60 \times 10^{-2}\) M.
To obtain results with good accuracy and precision the two wavelengths should be selected so that \(\varepsilon_X > \varepsilon_Y\) at one wavelength and \(\varepsilon_X < \varepsilon_Y\) at the other wavelength. It is easy to appreciate why this is true. Because the absorbance at each wavelength is dominated by one analyte, any uncertainty in the concentration of the other analyte has less of an impact. Figure \(\PageIndex{11}\) shows that the choice of wavelengths for Practice Exercise \(\PageIndex{2}\) are reasonable. When the choice of wavelengths is not obvious, one method for locating the optimum wavelengths is to plot \(\varepsilon_X / \varepsilon_y\) as function of wavelength, and determine the wavelengths where \(\varepsilon_X / \varepsilon_y\) reaches maximum and minimum values [Mehra, M. C.; Rioux, J. J. Chem. Educ. 1982, 59, 688–689].
When the analyte’s spectra overlap severely, such that \(\varepsilon_X \approx \varepsilon_Y\) at all wavelengths, other computational methods may provide better accuracy and precision. In a multiwavelength linear regression analysis, for example, a mixture’s absorbance is compared to that for a set of standard solutions at several wavelengths [Blanco, M.; Iturriaga, H.; Maspoch, S.; Tarin, P. J. Chem. Educ. 1989, 66, 178–180]. If ASX and ASY are the absorbance values for standard solutions of components X and Y at any wavelength, then
\[A_{SX}=\varepsilon_{X} b C_{SX} \label{10.3}\]
\[A_{SY}=\varepsilon_{Y} b C_{SY} \label{10.4}\]
where CSX and CSY are the known concentrations of X and Y in the standard solutions. Solving Equation \ref{10.3} and Equation \ref{10.4} for \(\varepsilon_X\) and for \(\varepsilon_Y\), substituting into Equation \ref{10.1}, and rearranging, gives
\[\frac{A_{\operatorname{mix}}}{A_{S X}}=\frac{C_{X}}{C_{S X}}+\frac{C_{Y}}{C_{S Y}} \times \frac{A_{S Y}}{A_{S X}} \nonumber\]
To determine CX and CY the mixture’s absorbance and the absorbances of the standard solutions are measured at several wavelengths. Graphing Amix/ASX versus ASY/ASX gives a straight line with a slope of CY/CSY and a y-intercept of CX/CSX. This approach is particularly helpful when it is not possible to find wavelengths where \(\varepsilon_X > \varepsilon_Y\) and \(\varepsilon_X < \varepsilon_Y\).
The approach outlined here for a multiwavelength linear regression uses a single standard solution for each analyte. A more rigorous approach uses multiple standards for each analyte. The math behind the analysis of such data—which we call a multiple linear regression—is beyond the level of this text. For more details about multiple linear regression see Brereton, R. G. Chemometrics: Data Analysis for the Laboratory and Chemical Plant, Wiley: Chichester, England, 2003.
Figure \(PageIndex{10.11}\) shows visible absorbance spectra for a standard solution of 0.0250 M Cr3+, a standard solution of 0.0750 M Co2+, and a mixture that contains unknown concentrations of each ion. The data for these spectra are shown here.
| \(\lambda\) (nm) | ACr | ACu | Amix | \(\lambda\) (nm) | ACr | ACu | Amix |
|---|---|---|---|---|---|---|---|
| 375 | 0.26 | 0.01 | 0.53 | 520 | 0.19 | 0.38 | 0.63 |
| 400 | 0.43 | 0.03 | 0.88 | 530 | 0.24 | 0.33 | 0.70 |
| 425 | 0.39 | 0.07 | 0.83 | 540 | 0.28 | 0.26 | 0.73 |
| 440 | 0.29 | 0.13 | 0.67 | 550 | 0.32 | 0.18 | 0.76 |
| 455 | 0.20 | 0.21 | 0.54 | 570 | 0.38 | 0.08 | 0.81 |
| 470 | 0.14 | 0.28 | 0.47 | 575 | 0.39 | 0.06 | 0.82 |
| 480 | 0.12 | 0.30 | 0.44 | 580 | 0.38 | 0.05 | 0.79 |
| 490 | 0.11 | 0.34 | 0.45 | 600 | 0.34 | 0.03 | 0.70 |
| 500 | 0.13 | 0.38 | 0.51 | 625 | 0.24 | 0.02 | 0.49 |
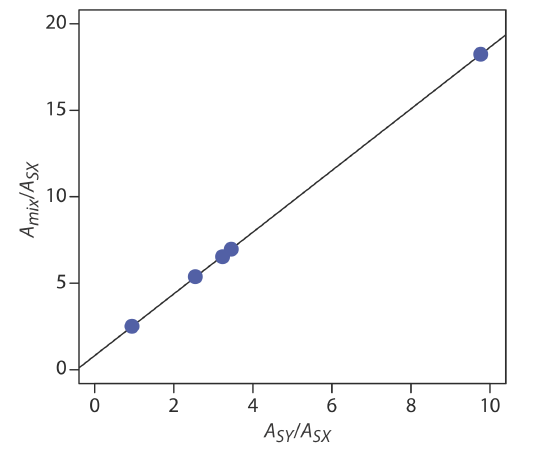
Use a multiwavelength regression analysis to determine the composition of the unknown.
Solution
First we need to calculate values for Amix/ASX and for ASY/ASX. Let’s define X as Co2+ and Y as Cr3+. For example, at a wavelength of 375 nm Amix/ASX is 0.53/0.01, or 53 and ASY/ASX is 0.26/0.01, or 26. Completing the calculation for all wavelengths and graphing Amix/ASX versus ASY/ASX gives the calibration curve shown in Figure \(\PageIndex{12}\). Fitting a straight-line to the data gives a regression model of
\[\frac{A_{\operatorname{mix}}}{A_{S X}}=0.636+2.01 \times \frac{A_{S Y}}{A_{S X}} \nonumber\]
Using the y-intercept, the concentration of Co2+ is
\[\frac{C_{X}}{C_{S X}}=\frac{\left[\mathrm{Co}^{2+}\right]}{0.0750 \mathrm{M}}=0.636 \nonumber\]
or [Co2+] = 0.048 M; using the slope the concentration of Cr3+ is
\[\frac{C_{Y}}{C_{S Y}}=\frac{\left[\mathrm{Cr}^{3+}\right]}{0.0250 \mathrm{M}}=2.01 \nonumber\]
or [Cr3+] = 0.050 M.
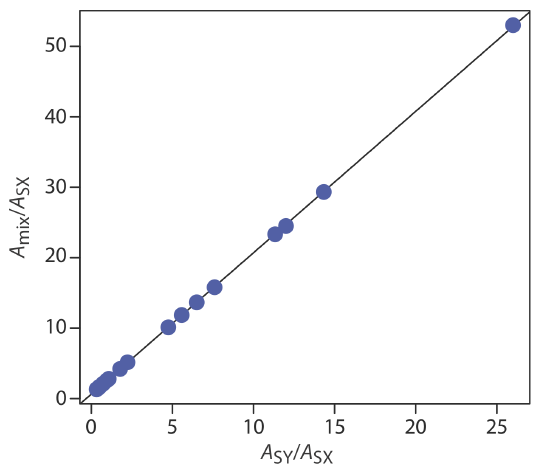
A mixture of \(\text{MnO}_4^{-}\) and \(\text{Cr}_2\text{O}_7^{2-}\), and standards of 0.10 mM KMnO4 and of 0.10 mM K2Cr2O7 give the results shown in the following table. Determine the composition of the mixture. The data for this problem is from Blanco, M. C.; Iturriaga, H.; Maspoch, S.; Tarin, P. J. Chem. Educ. 1989, 66, 178–180.
| \(\lambda\) (nm) | AMn | ACr | Amix |
|---|---|---|---|
| 266 | 0.042 | 0.410 | 0.766 |
| 288 | 0.082 | 0.283 | 0.571 |
| 320 | 0.168 | 0.158 | 0.422 |
| 350 | 0.125 | 0.318 | 0.672 |
| 360 | 0.036 | 0.181 | 0.366 |
- Answer
-
Letting X represent \(\text{MnO}_4^{-}\) and letting Y represent \(\text{Cr}_2\text{O}_7^{2-}\), we plot the equation
\[\frac{A_{\operatorname{mix}}}{A_{SX}}=\frac{C_{X}}{C_{SX}}+\frac{C_{Y}}{C_{S Y}} \times \frac{A_{S Y}}{A_{SX}} \nonumber\]
placing Amix/ASX on the y-axis and ASY/ASX on the x-axis. For example, at a wavelength of 266 nm the value Amix/ASX of is 0.766/0.042, or 18.2, and the value of ASY/ASX is 0.410/0.042, or 9.76. Completing the calculations for all wavelengths and plotting the data gives the result shown here
Fitting a straight-line to the data gives a regression model of
\[\frac{A_{\text { mix }}}{A_{\text { SX }}}=0.8147+1.7839 \times \frac{A_{SY}}{A_{SX}} \nonumber\]
Using the y-intercept, the concentration of \(\text{MnO}_4^{-}\) is
\[\frac{C_{X}}{C_{S X}}=0.8147=\frac{\left[\mathrm{MnO}_{4}^{-}\right]}{1.0 \times 10^{-4} \ \mathrm{M} \ \mathrm{MnO}_{4}^{-}} \nonumber\]
or \(8.15 \times 10^{-5}\) M \(\text{MnO}_4^{-}\), and using the slope, the concentration of \(\text{Cr}_2\text{O}_7^{2-}\) is
\[\frac{C_{Y}}{C_{S Y}}=1.7839=\frac{\left[\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\right]}{1.00 \times 10^{-4} \ \mathrm{M} \ \text{Cr}_{2} \mathrm{O}_{7}^{2-}} \nonumber\]
or \(1.78 \times 10^{-4}\) M \(\text{Cr}_2\text{O}_7^{2-}\).
Qualitative Applications
As discussed in Chapter 10.2, ultraviolet, visible, and infrared absorption bands result from the absorption of electromagnetic radiation by specific valence electrons or bonds. The energy at which the absorption occurs, and the intensity of that absorption, is determined by the chemical environment of the absorbing moiety. For example, benzene has several ultraviolet absorption bands due to \(\pi \rightarrow \pi^*\) transitions. The position and intensity of two of these bands, 203.5 nm (\(\varepsilon\) = 7400 M–1 cm–1) and 254 nm (\(\varepsilon\) = 204 M–1 cm–1), are sensitive to substitution. For benzoic acid, in which a carboxylic acid group replaces one of the aromatic hydrogens, the two bands shift to 230 nm (\(\varepsilon\) = 11600 M–1 cm–1) and 273 nm (\(\varepsilon\) = 970 M–1 cm–1). A variety of rules have been developed to aid in correlating UV/Vis absorption bands to chemical structure. Similar correlations are available for infrared absorption bands. For example a carbonyl’s C=O stretch is sensitive to adjacent functional groups, appearing at 1650 cm–1 for acids, 1700 cm–1 for ketones, and 1800 cm–1 for acid chlorides. The interpretation of UV/ Vis and IR spectra receives adequate coverage elsewhere in the chemistry curriculum, notably in organic chemistry, and is not considered further in this text.
With the availability of computerized data acquisition and storage it is possible to build digital libraries of standard reference spectra. The identity of an a unknown compound often can be determined by comparing its spectrum against a library of reference spectra, a process known as spectral searching. Comparisons are made using an algorithm that calculates the cumulative difference between the sample’s spectrum and a reference spectrum. For example, one simple algorithm uses the following equation
\[D = \sum_{i = 1}^n | (A_{sample})_i - (A_{reference})_i | \nonumber\]
where D is the cumulative difference, Asample is the sample’s absorbance at wavelength or wavenumber i, Areference is the absorbance of the reference compound at the same wavelength or wavenumber, and n is the number of digitized points in the spectra. The cumulative difference is calculated for each reference spectrum. The reference compound with the smallest value of D is the closest match to the unknown compound. The accuracy of spectral searching is limited by the number and type of compounds included in the library, and by the effect of the sample’s matrix on the spectrum.
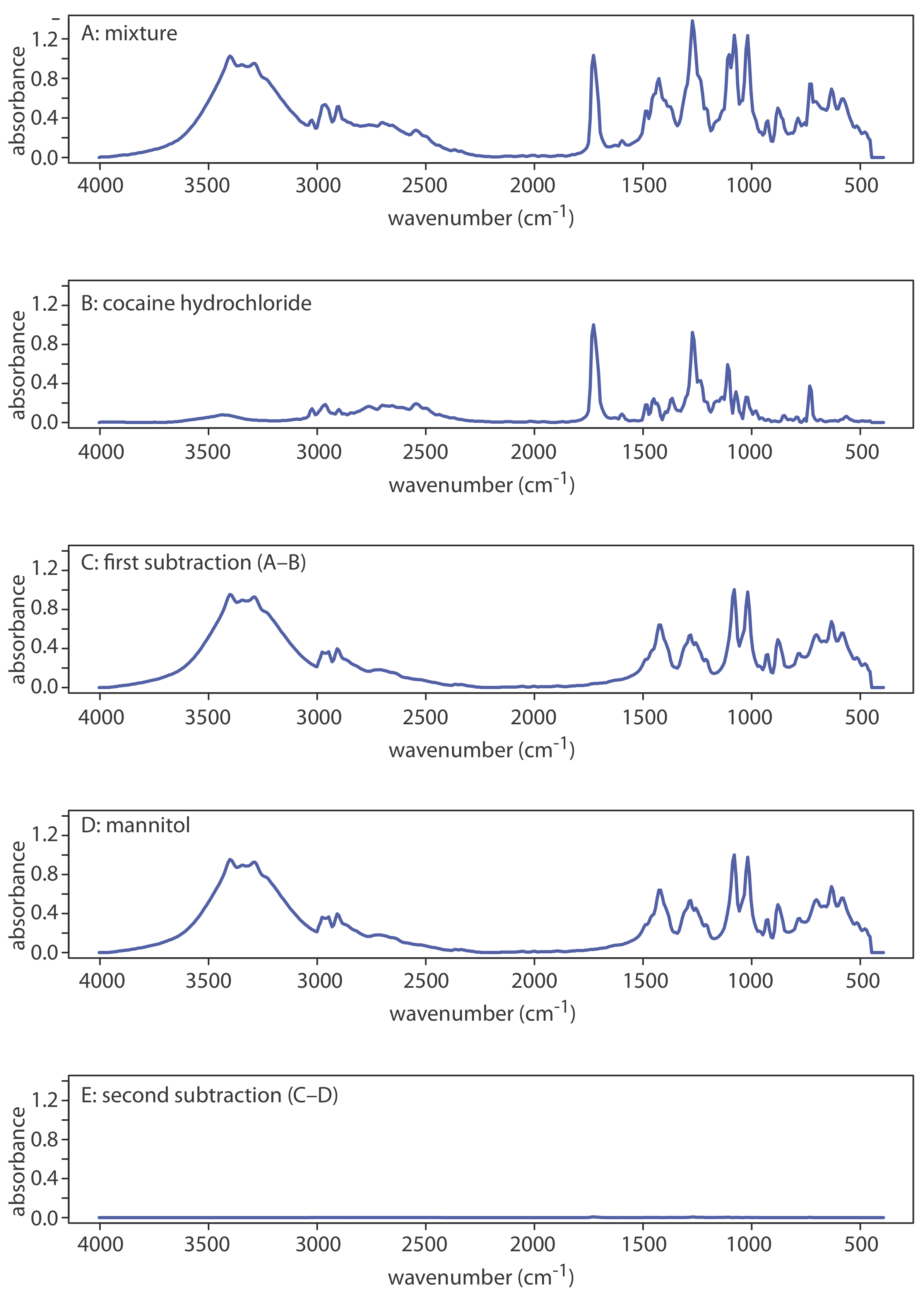
Another advantage of computerized data acquisition is the ability to subtract one spectrum from another. When coupled with spectral searching it is possible to determine the identity of several components in a sample without the need of a prior separation step by repeatedly searching and sub- tracting reference spectra. An example is shown in Figure \(\PageIndex{13}\) in which the composition of a two-component mixture is determined by successive searching and subtraction. Figure \(\PageIndex{13}\)a shows the spectrum of the mixture. A search of the spectral library selects cocaine•HCl (Figure \(\PageIndex{13}\)b) as a likely component of the mixture. Subtracting the reference spectrum for cocaine•HCl from the mixture’s spectrum leaves a result (Figure \(\PageIndex{13}\)c) that closely matches mannitol’s reference spectrum (Figure \(\PageIndex{13}\)d). Subtracting the reference spectrum for mannitol leaves a small residual signal (Figure \(\PageIndex{13}\)e).
Characterization Applications
Molecular absorption, particularly in the UV/Vis range, has been used for a variety of different characterization studies, including determining the stoichiometry of metal–ligand complexes and determining equilibrium constants. Both of these examples are examined in this section.
Stoichiometry of a Metal-Ligand Complex
We can determine the stoichiometry of the metal–ligand complexation reaction
\[\mathrm{M}+y \mathrm{L} \rightleftharpoons \mathrm{ML}_{y} \nonumber\]
using one of three methods: the method of continuous variations, the mole-ratio method, and the slope-ratio method. Of these approaches, the method of continuous variations, also called Job’s method, is the most popular. In this method a series of solutions is prepared such that the total moles of metal and of ligand, ntotal, in each solution is the same. If (nM)i and (nL)i are, respectively, the moles of metal and ligand in solution i, then
\[n_{\text { total }}=\ \left(n_{\mathrm{M}}\right)_{i} \ + \ \left(n_{\mathrm{L}}\right)_{i} \nonumber\]
The relative amount of ligand and metal in each solution is expressed as the mole fraction of ligand, (XL)i, and the mole fraction of metal, (XM)i,
\[\left(X_{\mathrm{L}}\right)_{i}=\frac{\left(n_{\mathrm{L}}\right)_{i}}{n_{\mathrm{total}}} \nonumber\]
\[\left(X_{M}\right)_{i}=1-\frac{\left(n_\text{L}\right)_{i}}{n_{\text { total }}}=\frac{\left(n_\text{M}\right)_{i}}{n_{\text { total }}} \nonumber\]
The concentration of the metal–ligand complex in any solution is determined by the limiting reagent, with the greatest concentration occurring when the metal and the ligand are mixed stoichiometrically. If we monitor the complexation reaction at a wavelength where only the metal–ligand complex absorbs, a graph of absorbance versus the mole fraction of ligand has two linear branches—one when the ligand is the limiting reagent and a second when the metal is the limiting reagent. The intersection of the two branches represents a stoichiometric mixing of the metal and the ligand. We use the mole fraction of ligand at the intersection to determine the value of y for the metal–ligand complex MLy.
\[y=\frac{n_{\mathrm{L}}}{n_{\mathrm{M}}}=\frac{X_{\mathrm{L}}}{X_{\mathrm{M}}}=\frac{X_{\mathrm{L}}}{1-X_{\mathrm{L}}} \nonumber\]
You also can plot the data as absorbance versus the mole fraction of metal. In this case, y is equal to (1 – XM)/XM.
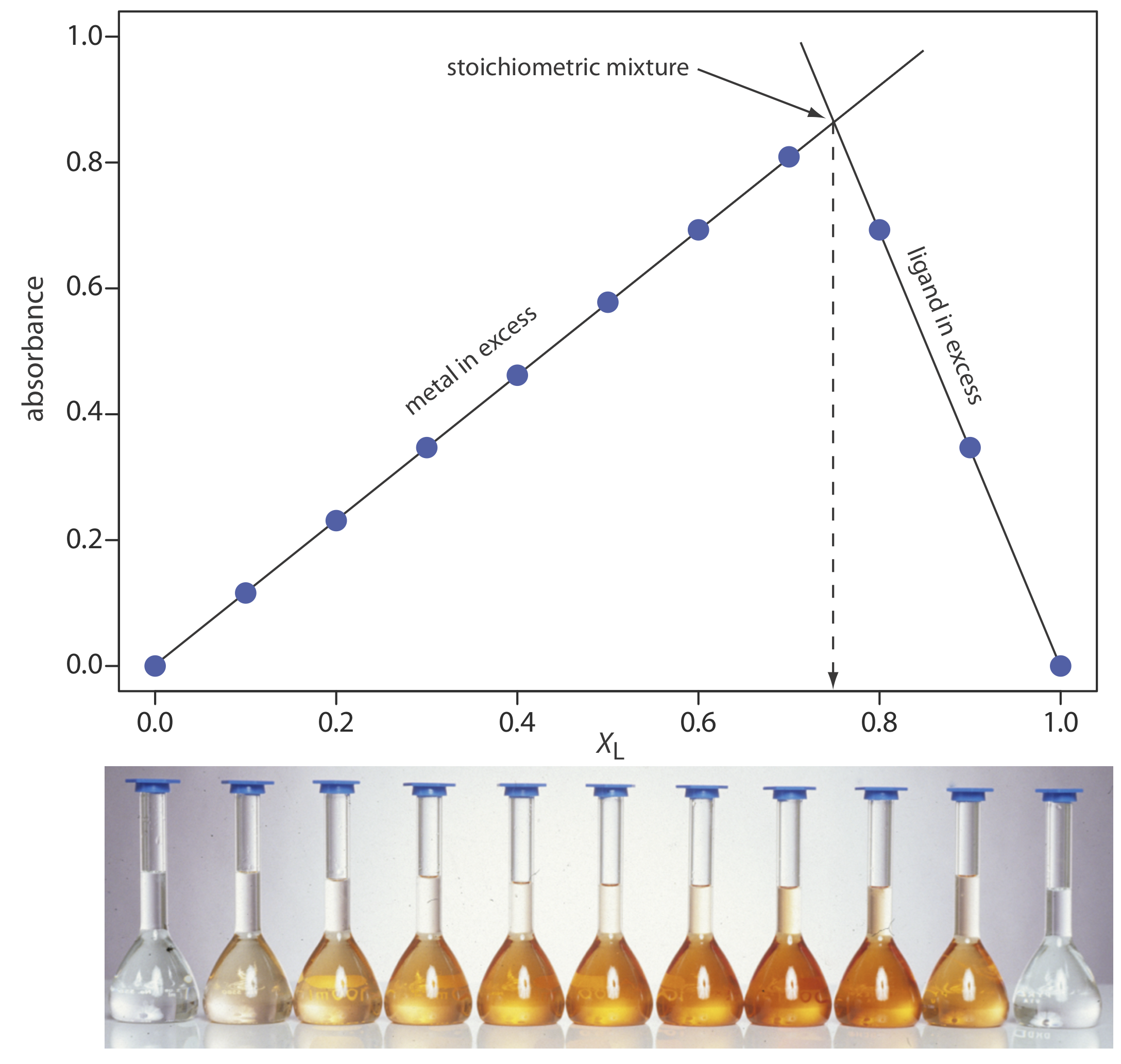
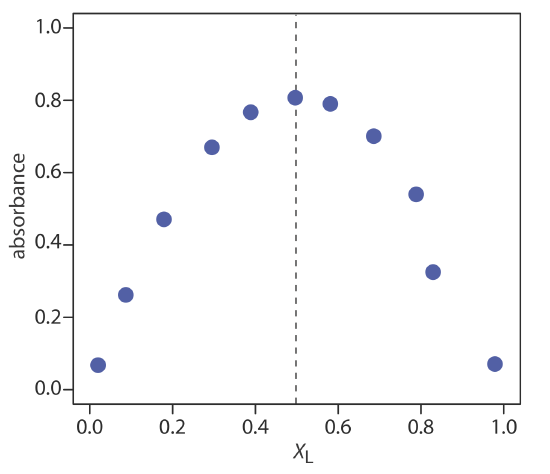
To determine the formula for the complex between Fe2+ and o-phenanthroline, a series of solutions is prepared in which the total concentration of metal and ligand is held constant at \(3.15 \times 10^{-4}\) M. The absorbance of each solution is measured at a wavelength of 510 nm. Using the following data, determine the formula for the complex.
| XL | absorbance | XL | absorbance |
|---|---|---|---|
| 0.000 | 0.000 | 0.600 | 0.693 |
| 0.100 | 0.116 | 0.700 | 0.809 |
| 0.200 | 0.231 | 0.800 | 0.693 |
| 0.300 | 0.347 | 0.900 | 0.347 |
| 0.400 | 0.462 | 1.000 | 0.000 |
| 0.500 | 0.578 |
Solution
A plot of absorbance versus the mole fraction of ligand is shown in Figure \(\PageIndex{14}\). To find the maximum absorbance, we extrapolate the two linear portions of the plot. The two lines intersect at a mole fraction of ligand of 0.75. Solving for y gives
\[y=\frac{X_{L}}{1-X_{L}}=\frac{0.75}{1-0.75}=3 \nonumber\]
The formula for the metal–ligand complex is \(\text{Fe(phen)}_3^{2+}\).
Use the continuous variations data in the following table to determine the formula for the complex between Fe2+ and SCN–. The data for this problem is adapted from Meloun, M.; Havel, J.; Högfeldt, E. Computation of Solution Equilibria, Ellis Horwood: Chichester, England, 1988, p. 236.
| XL | absorbance | XL | absorbance | XL | absorbance | XL | absorbance |
|---|---|---|---|---|---|---|---|
| 0.0200 | 0.068 | 0.2951 | 0.670 | 0.5811 | 0.790 | 0.8923 | 0.324 |
| 0.0870 | 0.262 | 0.3887 | 0.767 | 0.6860 | 0.701 | 0.9787 | 0.071 |
| 0.1792 | 0.471 | 0.4964 | 0.807 | 0.7885 | 0.540 |
- Answer
-
The figure below shows a continuous variations plot for the data in this exercise. Although the individual data points show substantial curvature—enough curvature that there is little point in trying to draw linear branches for excess metal and excess ligand—the maximum absorbance clearly occurs at XL ≈ 0.5. The complex’s stoichiometry, therefore, is Fe(SCN)2+.
Several precautions are necessary when using the method of continuous variations. First, the metal and the ligand must form only one metal–ligand complex. To determine if this condition is true, plots of absorbance versus XL are constructed at several different wavelengths and for several different values of ntotal. If the maximum absorbance does not occur at the same value of XL for each set of conditions, then more than one metal–ligand complex is present. A second precaution is that the metal–ligand complex’s absorbance must obey Beer’s law. Third, if the metal–ligand complex’s formation constant is relatively small, a plot of absorbance versus XL may show significant curvature. In this case it often is difficult to determine the stoichiometry by extrapolation. Finally, because the stability of a metal–ligand complex may be influenced by solution conditions, it is necessary to control carefully the composition of the solutions. When the ligand is a weak base, for example, each solutions must be buffered to the same pH.
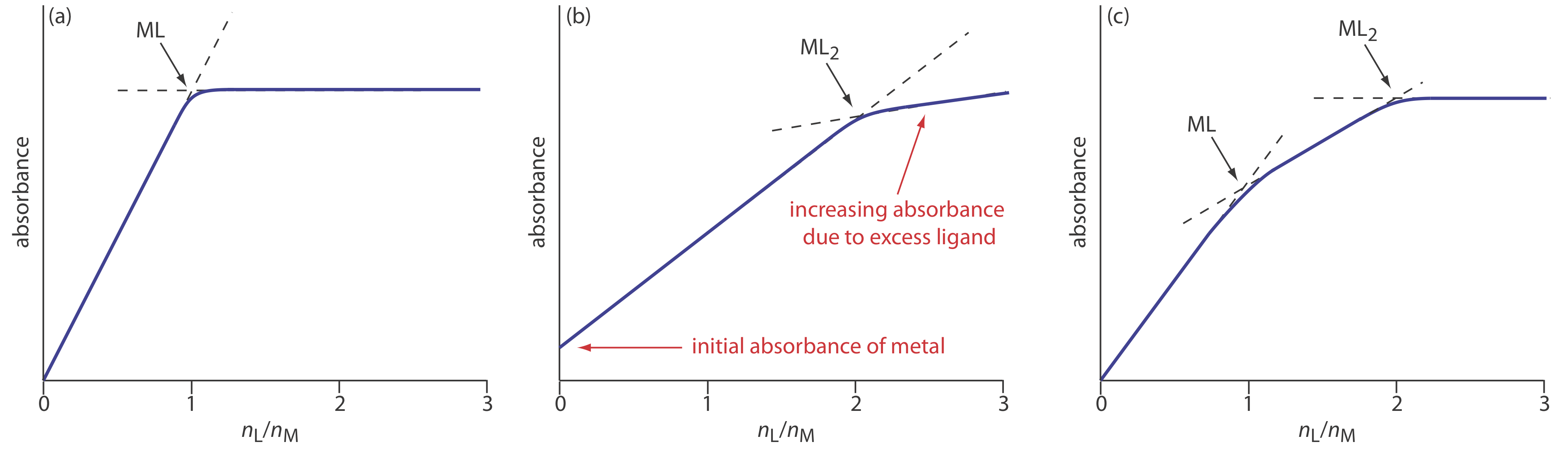
In the mole-ratio method the moles of one reactant, usually the metal, is held constant, while the moles of the other reactant is varied. The absorbance is monitored at a wavelength where the metal–ligand complex absorbs. A plot of absorbance as a function of the ligand-to-metal mole ratio, nL/nM, has two linear branches that intersect at a mole–ratio corresponding to the complex’s formula. Figure \(\PageIndex{15}\)a shows a mole-ratio plot for the formation of a 1:1 complex in which the absorbance is monitored at a wavelength where only the complex absorbs. Figure \(\PageIndex{15}\)b shows a mole-ratio plot for a 1:2 complex in which all three species—the metal, the ligand, and the complex—absorb at the selected wavelength. Unlike the method of continuous variations, the mole-ratio method can be used for complexation reactions that occur in a stepwise fashion if there is a difference in the molar absorptivities of the metal–ligand complexes, and if the formation constants are sufficiently different. A typical mole-ratio plot for the step-wise formation of ML and ML2 is shown in Figure \(\PageIndex{15}\)c.
For both the method of continuous variations and the mole-ratio method, we determine the complex’s stoichiometry by extrapolating absorbance data from conditions in which there is a linear relationship between absorbance and the relative amounts of metal and ligand. If a metal–ligand complex is very weak, a plot of absorbance versus XL or nL/nM becomes so curved that it is impossible to determine the stoichiometry by extrapolation. In this case the slope-ratio is used.
In the slope-ratio method two sets of solutions are prepared. The first set of solutions contains a constant amount of metal and a variable amount of ligand, chosen such that the total concentration of metal, CM, is much larger than the total concentration of ligand, CL. Under these conditions we may assume that essentially all the ligand reacts to form the metal–ligand complex. The concentration of the complex, which has the general form MxLy, is
\[\left[\mathrm{M}_{x} \mathrm{L_y}\right]=\frac{C_{\mathrm{L}}}{y} \nonumber\]
If we monitor the absorbance at a wavelength where only MxLy absorbs, then
\[A=\varepsilon b\left[\mathrm{M}_{x} \mathrm{L}_{y}\right]=\frac{\varepsilon b C_{\mathrm{L}}}{y} \nonumber\]
and a plot of absorbance versus CL is linear with a slope, sL, of
\[s_{\mathrm{L}}=\frac{\varepsilon b}{y} \nonumber\]
A second set of solutions is prepared with a fixed concentration of ligand that is much greater than a variable concentration of metal; thus
\[\left[\mathrm{M}_{x} \mathrm{L}_{y}\right]=\frac{C_{\mathrm{M}}}{x} \nonumber\]
\[A=\varepsilon b\left[\mathrm{M}_{x} \mathrm{L}_{y}\right]=\frac{\varepsilon b C_{\mathrm{M}}}{x} \nonumber\]
\[s_{M}=\frac{\varepsilon b}{x} \nonumber\]
A ratio of the slopes provides the relative values of x and y.
\[\frac{s_{\text{M}}}{s_{\text{L}}}=\frac{\varepsilon b / x}{\varepsilon b / y}=\frac{y}{x} \nonumber\]
An important assumption in the slope-ratio method is that the complexation reaction continues to completion in the presence of a sufficiently large excess of metal or ligand. The slope-ratio method also is limited to systems in which only a single complex forms and for which Beer’s law is obeyed.
Determination of Equilibrium Constants
Another important application of molecular absorption spectroscopy is the determination of equilibrium constants. Let’s consider, as a simple example, an acid–base reaction of the general form
\[\operatorname{HIn}(a q)+ \ \mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \ \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\operatorname{In}^{-}(a q) \nonumber\]
where HIn and In– are the conjugate weak acid and weak base forms of an acid–base indicator. The equilibrium constant for this reaction is
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{A^-}]}{[\mathrm{HA}]} \nonumber\]
To determine the equilibrium constant’s value, we prepare a solution in which the reaction is in a state of equilibrium and determine the equilibrium concentration for H3O+, HIn, and In–. The concentration of H3O+ is easy to determine by measuring the solution’s pH. To determine the concentration of HIn and In– we can measure the solution’s absorbance.
If both HIn and In– absorb at the selected wavelength, then, from Beer's law, we know that
\[A=\varepsilon_{\mathrm{Hln}} b[\mathrm{HIn}]+\varepsilon_{\mathrm{ln}} b[\mathrm{In}^-] \label{10.5}\]
where \(\varepsilon_\text{HIn}\) and \(\varepsilon_{\text{In}}\) are the molar absorptivities for HIn and In–. The indicator’s total concentration, C, is given by a mass balance equation
\[C=[\mathrm{HIn}]+ [\text{In}^-] \label{10.6}\]
Solving Equation \ref{10.6} for [HIn] and substituting into Equation \ref{10.5} gives
\[A=\varepsilon_{\mathrm{Hln}} b\left(C-\left[\mathrm{In}^{-}\right]\right)+\varepsilon_{\mathrm{ln}} b\left[\mathrm{In}^{-}\right] \nonumber\]
which we simplify to
\[A=\varepsilon_{\mathrm{Hln}} bC- \varepsilon_{\mathrm{Hln}}b\left[\mathrm{In}^{-}\right]+\varepsilon_{\mathrm{ln}} b\left[\mathrm{In}^{-}\right] \nonumber\]
\[A=A_{\mathrm{HIn}}+b\left[\operatorname{In}^{-}\right]\left(\varepsilon_{\mathrm{ln}}-\varepsilon_{\mathrm{HIn}}\right) \label{10.7}\]
where AHIn, which is equal to \(\varepsilon_\text{HIn}bC\), is the absorbance when the pH is acidic enough that essentially all the indicator is present as HIn. Solving Equation \ref{10.7} for the concentration of In– gives
\[\left[\operatorname{In}^{-}\right]=\frac{A-A_{\mathrm{Hln}}}{b\left(\varepsilon_{\mathrm{ln}}-\varepsilon_{\mathrm{HIn}}\right)} \label{10.8}\]
Proceeding in the same fashion, we derive a similar equation for the concentration of HIn
\[[\mathrm{HIn}]=\frac{A_{\mathrm{In}}-A}{b\left(\varepsilon_{\mathrm{ln}}-\varepsilon_{\mathrm{Hln}}\right)} \label{10.9}\]
where AIn, which is equal to \(\varepsilon_{\text{In}}bC\), is the absorbance when the pH is basic enough that only In– contributes to the absorbance. Substituting Equation \ref{10.8} and Equation \ref{10.9} into the equilibrium constant expression for HIn gives
\[K_a = \frac {[\text{H}_3\text{O}^+][\text{In}^-]} {[\text{HIn}]} = [\text{H}_3\text{O}^+] \times \frac {A - A_\text{HIn}} {A_{\text{In}} - A} \label{10.10}\]
We can use Equation \ref{10.10} to determine Ka in one of two ways. The simplest approach is to prepare three solutions, each of which contains the same amount, C, of indicator. The pH of one solution is made sufficiently acidic such that [HIn] >> [In–]. The absorbance of this solution gives AHIn. The value of AIn is determined by adjusting the pH of the second solution such that [In–] >> [HIn]. Finally, the pH of the third solution is adjusted to an intermediate value, and the pH and absorbance, A, recorded. The value of Ka is calculated using Equation \ref{10.10}.
The acidity constant for an acid–base indicator is determined by preparing three solutions, each of which has a total concentration of indicator equal to \(5.00 \times 10^{-5}\) M. The first solution is made strongly acidic with HCl and has an absorbance of 0.250. The second solution is made strongly basic and has an absorbance of 1.40. The pH of the third solution is 2.91 and has an absorbance of 0.662. What is the value of Ka for the indicator?
Solution
The value of Ka is determined by making appropriate substitutions into 10.20 where [H3O+] is \(1.23 \times 10^{-3}\); thus
\[K_{\mathrm{a}}=\left(1.23 \times 10^{-3}\right) \times \frac{0.662-0.250}{1.40-0.662}=6.87 \times 10^{-4} \nonumber\]
To determine the Ka of a merocyanine dye, the absorbance of a solution of \(3.5 \times 10^{-4}\) M dye was measured at a pH of 2.00, a pH of 6.00, and a pH of 12.00, yielding absorbances of 0.000, 0.225, and 0.680, respectively. What is the value of Ka for this dye? The data for this problem is adapted from Lu, H.; Rutan, S. C. Anal. Chem., 1996, 68, 1381–1386.
- Answer
-
The value of Ka is
\[K_{\mathrm{a}}=\left(1.00 \times 10^{-6}\right) \times \frac{0.225-0.000}{0.680-0.225}=4.95 \times 10^{-7} \nonumber\]
A second approach for determining Ka is to prepare a series of solutions, each of which contains the same amount of indicator. Two solutions are used to determine values for AHIn and AIn. Taking the log of both sides of Equation \ref{10.10} and rearranging leave us with the following equation.
\[\log \frac{A-A_{\mathrm{Hin}}}{A_{\mathrm{ln}^{-}}-A}=\mathrm{pH}-\mathrm{p} K_{\mathrm{a}} \label{10.11}\]
A plot of log[(A – AHIn)/(AIn – A)] versus pH is a straight-line with a slope of +1 and a y-intercept of –pKa.
To determine the Ka for the indicator bromothymol blue, the absorbance of each a series of solutions that contain the same concentration of bromothymol blue is measured at pH levels of 3.35, 3.65, 3.94, 4.30, and 4.64, yielding absorbance values of 0.170, 0.287, 0.411, 0.562, and 0.670, respectively. Acidifying the first solution to a pH of 2 changes its absorbance to 0.006, and adjusting the pH of the last solution to 12 changes its absorbance to 0.818. What is the value of Ka for bromothymol blue? The data for this problem is from Patterson, G. S. J. Chem. Educ., 1999, 76, 395–398.
- Answer
-
To determine Ka we use Equation \ref{10.11}, plotting log[(A – AHIn)/(AIn – A)] versus pH, as shown below.
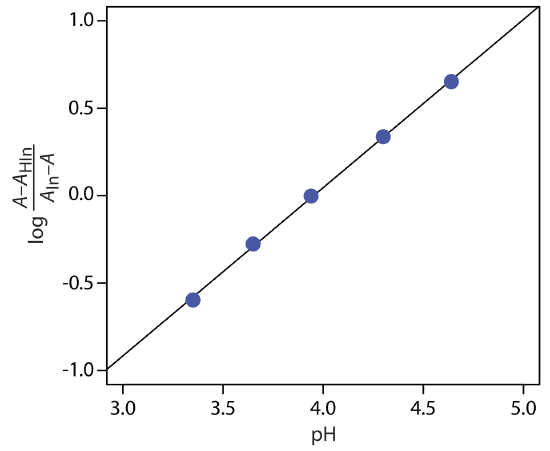
Fitting a straight-line to the data gives a regression model of
\[\log \frac{A-A_{\mathrm{HIn}}}{A_{\mathrm{ln}}-A}=-3.80+0.962 \mathrm{pH} \nonumber\]
The y-intercept is –pKa; thus, the pKa is 3.80 and the Ka is \(1.58 \times 10^{-4}\).
In developing these approaches for determining Ka we considered a relatively simple system in which the absorbance of HIn and In– are easy to measure and for which it is easy to determine the concentration of H3O+. In addition to acid–base reactions, we can adapt these approaches to any reaction of the general form
\[X(a q)+Y(a q)\rightleftharpoons Z(a q) \nonumber\]
including metal–ligand complexation reactions and redox reactions, provided we can determine spectrophotometrically the concentration of the product, Z, and one of the reactants, either X or Y, and that we can determine the concentration of the other reactant by some other method. With appropriate modifications, a more complicated system in which we cannot determine the concentration of one or more of the reactants or products also is possible [Ramette, R. W. Chemical Equilibrium and Analysis, Addison-Wesley: Reading, MA, 1981, Chapter 13].
Evaluation of UV/Vis and IR Spectroscopy
Scale of Operations
Molecular UV/Vis absorption routinely is used for the analysis of trace analytes in macro and meso samples. Major and minor analytes are determined by diluting the sample before analysis, and concentrating a sample may allow for the analysis of ultratrace analytes. The scale of operations for infrared absorption is generally poorer than that for UV/Vis absorption.
Accuracy
Under normal conditions a relative error of 1–5% is easy to obtained with UV/Vis absorption. Accuracy usually is limited by the quality of the blank. Examples of the type of problems that are encountered include the pres- ence of particulates in the sample that scatter radiation, and the presence of interferents that react with analytical reagents. In the latter case the interferent may react to form an absorbing species, which leads to a positive determinate error. Interferents also may prevent the analyte from reacting, which leads to a negative determinate error. With care, it is possible to improve the accuracy of an analysis by as much as an order of magnitude.
Precision
In absorption spectroscopy, precision is limited by indeterminate errors—primarily instrumental noise—which are introduced when we measure absorbance. Precision generally is worse for low absorbances where P0 ≈ PT, and for high absorbances where PT approaches 0. We might expect, therefore, that precision will vary with transmittance.
We can derive an expression between precision and transmittance by applying the propagation of uncertainty as described in Chapter 4. To do so we rewrite Beer’s law as
\[C=-\frac{1}{\varepsilon b} \log T \label{10.12}\]
Table 4.3.1 in Chapter 4 helps us complete the propagation of uncertainty for Equation \ref{10.12}; thus, the absolute uncertainty in the concentration, sC, is
\[s_{c}=-\frac{0.4343}{\varepsilon b} \times \frac{s_{T}}{T} \label{10.13}\]
where sT is the absolute uncertainty in the transmittance. Dividing Equation \ref{10.13} by Equation \ref{10.12} gives the relative uncertainty in concentration, sC/C, as
\[\frac{s_c}{C}=\frac{0.4343 s_{T}}{T \log T} \nonumber\]
If we know the transmittance’s absolute uncertainty, then we can determine the relative uncertainty in concentration for any measured transmittance.
Determining the relative uncertainty in concentration is complicated because sT is a function of the transmittance. As shown in Table \(\PageIndex{3}\), three categories of indeterminate instrumental error are observed [Rothman, L. D.; Crouch, S. R.; Ingle, J. D. Jr. Anal. Chem. 1975, 47, 1226–1233]. A constant sT is observed for the uncertainty associated with reading %T on a meter’s analog or digital scale. Typical values are ±0.2–0.3% (a k1 of ±0.002–0.003) for an analog scale and ±0.001% a (k1 of ±0.00001) for a digital scale.
A constant sT also is observed for the thermal transducers used in infrared spectrophotometers. The effect of a constant sT on the relative uncertainty in concentration is shown by curve A in Figure \(\PageIndex{16}\). Note that the relative uncertainty is very large for both high absorbances and low absorbances, reaching a minimum when the absorbance is 0.4343. This source of indeterminate error is important for infrared spectrophotometers and for inexpensive UV/Vis spectrophotometers. To obtain a relative uncertainty in concentration of ±1–2%, the absorbance is kept within the range 0.1–1.
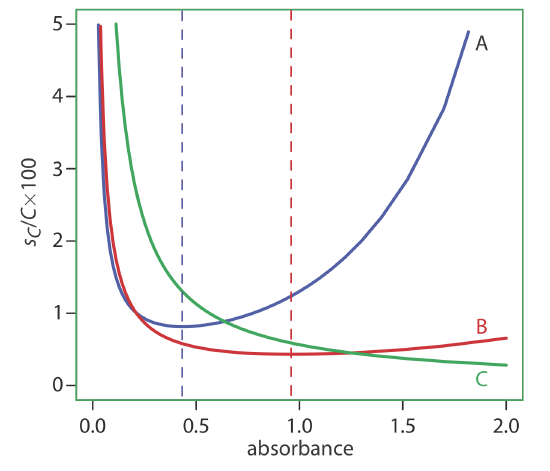
Values of sT are a complex function of transmittance when indeterminate errors are dominated by the noise associated with photon detectors. Curve B in Figure \(\PageIndex{16}\) shows that the relative uncertainty in concentration is very large for low absorbances, but is smaller at higher absorbances. Although the relative uncertainty reaches a minimum when the absorbance is 0.963, there is little change in the relative uncertainty for absorbances between 0.5 and 2. This source of indeterminate error generally limits the precision of high quality UV/Vis spectrophotometers for mid-to-high absorbances.
Finally, the value of sT is directly proportional to transmittance for indeterminate errors that result from fluctuations in the source’s intensity and from uncertainty in positioning the sample within the spectrometer. The latter is particularly important because the optical properties of a sample cell are not uniform. As a result, repositioning the sample cell may lead to a change in the intensity of transmitted radiation. As shown by curve C in Figure \(\PageIndex{16}\), the effect is important only at low absorbances. This source of indeterminate errors usually is the limiting factor for high quality UV/Vis spectrophotometers when the absorbance is relatively small.
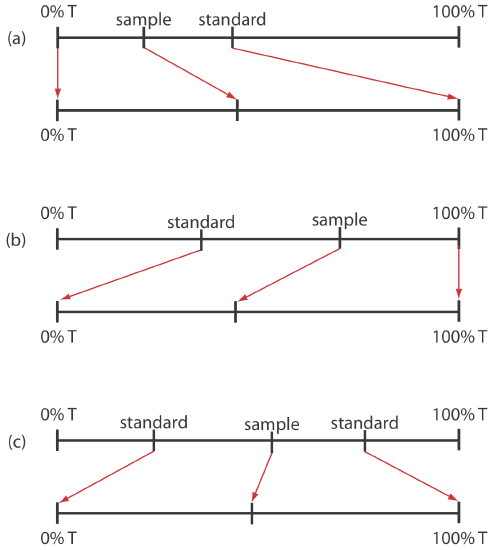
When the relative uncertainty in concentration is limited by the %T readout resolution, it is possible to improve the precision of the analysis by redefining 100% T and 0% T. Normally 100% T is established using a blank and 0% T is established while preventing the source’s radiation from reaching the detector. If the absorbance is too high, precision is improved by resetting 100% T using a standard solution of analyte whose concentration is less than that of the sample (Figure \(\PageIndex{17}\)a). For a sample whose absorbance is too low, precision is improved by redefining 0% T using a standard solution of the analyte whose concentration is greater than that of the analyte (Figure \(\PageIndex{17}\)b). In this case a calibration curve is required because a linear relationship between absorbance and concentration no longer exists. Precision is further increased by combining these two methods (Figure \(\PageIndex{17}\)c). Again, a calibration curve is necessary since the relation- ship between absorbance and concentration is no longer linear.
Sensitivity
The sensitivity of a molecular absorption method, which is the slope of a Beer’s law calibration curve, is the product of the analyte’s absorptivity and the pathlength of the sample cell (\(\varepsilon b\)). You can improve a method’s sensitivity by selecting a wavelength where absorbance is at a maximum or by increasing pathlength.
See Figure 10.2.10 for an example of how the choice of wavelength affects a calibration curve’s sensitivity.
Selectivity
Selectivity rarely is a problem in molecular absorption spectrophotometry. In many cases it is possible to find a wavelength where only the analyte absorbs. When two or more species do contribute to the measured absorbance, a multicomponent analysis is still possible, as shown in Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
Time, Cost, and Equipment
The analysis of a sample by molecular absorption spectroscopy is relatively rapid, although additional time is required if we need to convert a nonabsorbing analyte into an absorbing form. The cost of UV/Vis instrumentation ranges from several hundred dollars for a simple filter photometer, to more than $50,000 for a computer-controlled, high-resolution double-beam instrument equipped with variable slit widths, and operating over an extended range of wavelengths. Fourier transform infrared spectrometers can be obtained for as little as $15,000–$20,000, although more expensive models are available.


