10.2: Spectroscopy Based on Absorption
- Page ID
- 157673
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In absorption spectroscopy a beam of electromagnetic radiation passes through a sample. Much of the radiation passes through the sample without a loss in intensity. At selected wavelengths, however, the radiation’s intensity is attenuated. This process of attenuation is called absorption.
Absorption Spectra
There are two general requirements for an analyte’s absorption of electromagnetic radiation. First, there must be a mechanism by which the radiation’s electric field or magnetic field interacts with the analyte. For ultraviolet and visible radiation, absorption of a photon changes the energy of the analyte’s valence electrons. A bond’s vibrational energy is altered by the absorption of infrared radiation.
Figure 10.1.3 provides a list of the types of atomic and molecular transitions associated with different types of electromagnetic radiation.
The second requirement is that the photon’s energy, \(h \nu\), must exactly equal the difference in energy, \(\Delta E\), between two of the analyte’s quantized energy states. Figure 10.1.4 shows a simplified view of a photon’s absorption, which is useful because it emphasizes that the photon’s energy must match the difference in energy between a lower-energy state and a higher-energy state. What is missing, however, is information about what types of energy states are involved, which transitions between energy states are likely to occur, and the appearance of the resulting spectrum.
We can use the energy level diagram in Figure 10.2.1 to explain an absorbance spectrum. The lines labeled E0 and E1 represent the analyte’s ground (lowest) electronic state and its first electronic excited state. Superimposed on each electronic energy level is a series of lines representing vibrational energy levels.

Infrared Spectra for Molecules and Polyatomic Ions
The energy of infrared radiation produces a change in a molecule’s or a polyatomic ion’s vibrational energy, but is not sufficient to effect a change in its electronic energy. As shown in Figure 10.2.1 , vibrational energy levels are quantized; that is, a molecule or polyatomic ion has only certain, discrete vibrational energies. The energy for an allowed vibrational mode, \(E_{\nu}\), is
\[E_{\nu}=\nu+\frac{1}{2} h \nu_{0} \nonumber\]
where \(\nu\) is the vibrational quantum number, which has values of 0, 1, 2, ..., and \(\nu_0\) is the bond’s fundamental vibrational frequency. The value of \(\nu_0\), which is determined by the bond’s strength and by the mass at each end of the bond, is a characteristic property of a bond. For example, a carbon-carbon single bond (C–C) absorbs infrared radiation at a lower energy than a carbon-carbon double bond (C=C) because a single bond is weaker than a double bond.
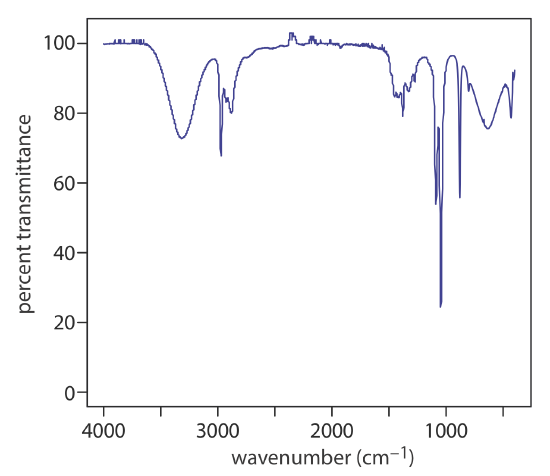
At room temperature most molecules are in their ground vibrational state (\(\nu = 0\)) . A transition from the ground vibrational state to the first vibrational excited state (\(\nu = 1\)) requires absorption of a photon with an energy of \(h \nu_0\). Transitions in which \(\Delta \nu = \pm 1\) give rise to the fundamental absorption lines. Weaker absorption lines, called overtones, result from transitions in which \(\Delta \nu\) is ±2 or ±3. The number of possible normal vibrational modes for a linear molecule is 3N – 5, and for a non-linear molecule is 3N – 6, where N is the number of atoms in the molecule. Not surprisingly, infrared spectra often show a considerable number of absorption bands. Even a relatively simple molecule, such as ethanol (C2H6O), for example, has \(3 \times 9 - 6\), or 21 possible normal modes of vibration, although not all of these vibrational modes give rise to an absorption. The IR spectrum for ethanol is shown in Figure 10.2.2 .
Why does a non-linear molecule have 3N – 6 vibrational modes? Consider a molecule of methane, CH4. Each of methane’s five atoms can move in one of three directions (x, y, and z) for a total of \(5 \times 3 = 15\) different ways in which the molecule’s atoms can move. A molecule can move in three ways: it can move from one place to another, which we call translational motion; it can rotate around an axis, which we call rotational motion; and its bonds can stretch and bend, which we call vibrational motion. Because the entire molecule can move in the x, y, and z directions, three of methane’s 15 different motions are translational. In addition, the molecule can rotate about its x, y, and z axes, accounting for three additional forms of motion. This leaves 15 – 3 – 3 = 9 vibrational modes. A linear molecule, such as CO2, has 3N – 5 vibrational modes because it can rotate around only two axes.
UV/Vis Spectra for Molecules and Ions
The valence electrons in organic molecules and polyatomic ions, such as \(\text{CO}_3^{2-}\), occupy quantized sigma bonding (\(\sigma\)), pi bonding (\(\pi\)), and non-bonding (n) molecular orbitals (MOs). Unoccupied sigma antibonding (\(\sigma^*\)) and pi antibonding (\(\pi^*\)) molecular orbitals are slightly higher in energy. Because the difference in energy between the highest-energy occupied MOs and the lowest-energy unoccupied MOs corresponds to ultraviolet and visible radiation, absorption of a photon is possible.
Four types of transitions between quantized energy levels account for most molecular UV/Vis spectra. Table 10.2.1 lists the approximate wavelength ranges for these transitions, as well as a partial list of bonds, functional groups, or molecules responsible for these transitions. Of these transitions, the most important are \(n \rightarrow \pi^*\) and \(\pi \rightarrow \pi^*\) because they involve important functional groups that are characteristic of many analytes and because the wavelengths are easily accessible. The bonds and functional groups that give rise to the absorption of ultraviolet and visible radiation are called chromophores.
Many transition metal ions, such as Cu2+ and Co2+, form colorful solutions because the metal ion absorbs visible light. The transitions that give rise to this absorption are valence electrons in the metal ion’s d-orbitals. For a free metal ion, the five d-orbitals are of equal energy. In the presence of a complexing ligand or solvent molecule, however, the d-orbitals split into two or more groups that differ in energy. For example, in an octahedral complex of \(\text{Cu(H}_2\text{O)}_6^{2+}\) the six water molecules perturb the d-orbitals into the two groups shown in Figure 10.2.3 . The resulting \(d \rightarrow d\) transitions for transition metal ions are relatively weak.
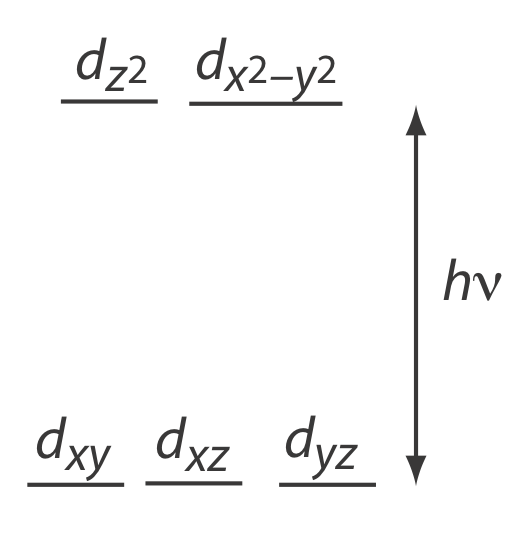
A more important source of UV/Vis absorption for inorganic metal–ligand complexes is charge transfer, in which absorption of a photon produces an excited state in which there is transfer of an electron from the metal, M, to the ligand, L.
\[M-L+h \nu \rightarrow\left(M^{+}-L^{-}\right)^{*} \nonumber\]
Charge-transfer absorption is important because it produces very large absorbances. One important example of a charge-transfer complex is that of o-phenanthroline with Fe2+, the UV/Vis spectrum for which is shown in Figure 10.2.4 . Charge-transfer absorption in which an electron moves from the ligand to the metal also is possible.
Why is a larger absorbance desirable? An analytical method is more sensitive if a smaller concentration of analyte gives a larger signal.
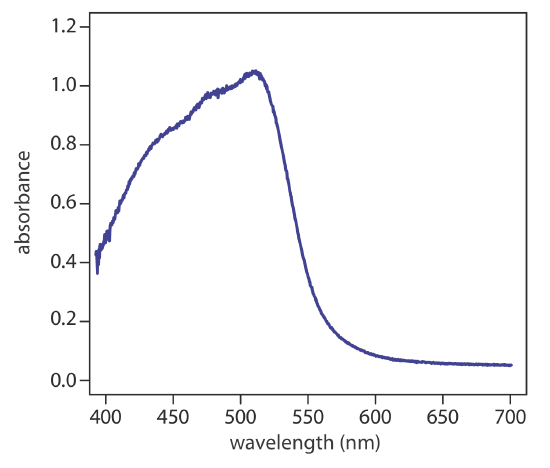
Comparing the IR spectrum in Figure 10.2.2 to the UV/Vis spectrum in Figure 10.2.4 shows us that UV/Vis absorption bands are often significantly broader than those for IR absorption. We can use Figure 10.2.1 to explain why this is true. When a species absorbs UV/Vis radiation, the transition between electronic energy levels may also include a transition between vibrational energy levels. The result is a number of closely spaced absorption bands that merge together to form a single broad absorption band.
UV/Vis Spectra for Atoms
The energy of ultraviolet and visible electromagnetic radiation is sufficient to cause a change in an atom’s valence electron configuration. Sodium, for example, has a single valence electron in its 3s atomic orbital. As shown in Figure 10.2.5 , unoccupied, higher energy atomic orbitals also exist.
The valence shell energy level diagram in Figure 10.2.5 might strike you as odd because it shows that the 3p orbitals are split into two groups of slightly different energy. The reasons for this splitting are unimportant in the context of our treatment of atomic absorption. For further information about the reasons for this splitting, consult the chapter’s additional resources.
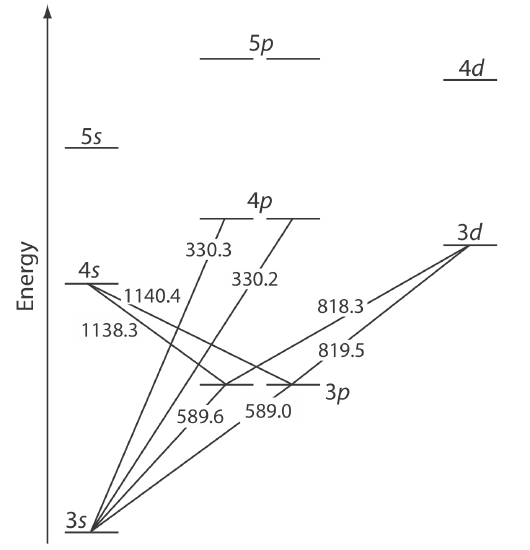
Absorption of a photon is accompanied by the excitation of an electron from a lower-energy atomic orbital to an atomic orbital of higher energy. Not all possible transitions between atomic orbitals are allowed. For sodium the only allowed transitions are those in which there is a change of ±1 in the orbital quantum number (l); thus transitions from \(s \rightarrow p\) orbitals are allowed, but transitions from \(s \rightarrow s\) and from \(s \rightarrow d\) orbitals are forbidden.
The atomic absorption spectrum for Na is shown in Figure 10.2.6 , and is typical of that found for most atoms. The most obvious feature of this spectrum is that it consists of a small number of discrete absorption lines that correspond to transitions between the ground state (the 3s atomic orbital) and the 3p and the 4p atomic orbitals. Absorption from excited states, such as the \(3p \rightarrow 4s\) and the \(3p \rightarrow 3d\) transitions included in Figure 10.2.5 , are too weak to detect. Because an excited state’s lifetime is short—an excited state atom typically returns to a lower energy state in 10–7 to 10–8 seconds—an atom in the exited state is likely to return to the ground state before it has an opportunity to absorb a photon.
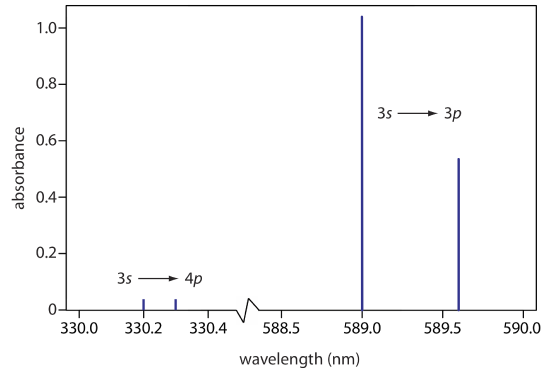
Another feature of the atomic absorption spectrum in Figure 10.2.6 is the narrow width of the absorption lines, which is a consequence of the fixed difference in energy between the ground state and the excited state, and the lack of vibrational and rotational energy levels. Natural line widths for atomic absorption, which are governed by the uncertainty principle, are approximately 10–5 nm. Other contributions to broadening increase this line width to approximately 10–3 nm.
Transmittance and Absorbance
As light passes through a sample, its power decreases as some of it is absorbed. This attenuation of radiation is described quantitatively by two separate, but related terms: transmittance and absorbance. As shown in Figure 10.2.7 a, transmittance is the ratio of the source radiation’s power as it exits the sample, PT, to that incident on the sample, P0.
\[T=\frac{P_{\mathrm{T}}}{P_{0}} \label{10.1}\]
Multiplying the transmittance by 100 gives the percent transmittance, %T, which varies between 100% (no absorption) and 0% (complete absorption). All methods of detecting photons—including the human eye and modern photoelectric transducers—measure the transmittance of electromagnetic radiation.
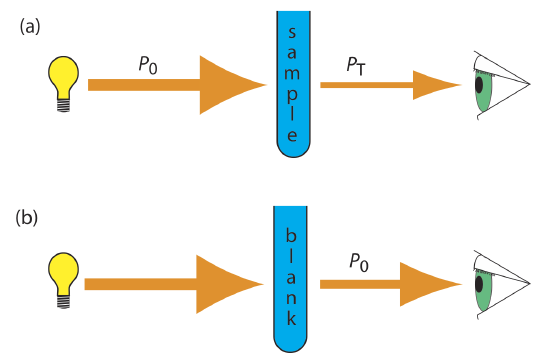
Equation \ref{10.1} does not distinguish between different mechanisms that prevent a photon emitted by the source from reaching the detector. In addition to absorption by the analyte, several additional phenomena contribute to the attenuation of radiation, including reflection and absorption by the sample’s container, absorption by other components in the sample’s matrix, and the scattering of radiation. To compensate for this loss of the radiation’s power, we use a method blank. As shown in Figure 10.2.7 b, we redefine P0 as the power exiting the method blank.
An alternative method for expressing the attenuation of electromagnetic radiation is absorbance, A, which we define as
\[A=-\log T=-\log \frac{P_{\mathrm{T}}}{P_{0}} \label{10.2}\]
Absorbance is the more common unit for expressing the attenuation of radiation because it is a linear function of the analyte’s concentration.
We will show that this is true in the next section when we introduce Beer’s law.
A sample has a percent transmittance of 50%. What is its absorbance?
Solution
A percent transmittance of 50.0% is the same as a transmittance of 0.500. Substituting into Equation \ref{10.2} gives
\[A=-\log T=-\log (0.500)=0.301 \nonumber\]
What is the %T for a sample if its absorbance is 1.27?
- Answer
-
To find the transmittance, T, we begin by noting that
\[A=1.27=-\log T \nonumber\]
Solving for T
\[\begin{array}{c}{-1.27=\log T} \\ {10^{-1.27}=T}\end{array} \nonumber\]
gives a transmittance of 0.054, or a %T of 5.4%.
Equation \ref{10.1} has an important consequence for atomic absorption. As we learned from Figure 10.2.6 , atomic absorption lines are very narrow. Even with a high quality monochromator, the effective bandwidth for a continuum source is \(100-1000 \times\) greater than the width of an atomic absorption line. As a result, little radiation from a continuum source is absorbed when it passes through a sample of atoms; because P0 ≈ PT the measured absorbance effectively is zero. For this reason, atomic absorption requires that we use a line source instead of a continuum source.
Absorbance and Concentration: Beer's Law
When monochromatic electromagnetic radiation passes through an infinitesimally thin layer of sample of thickness dx, it experiences a decrease in its power of dP (Figure 10.2.8 ).

This fractional decrease in power is proportional to the sample’s thickness and to the analyte’s concentration, C; thus
\[-\frac{d P}{P}=\alpha C d x \label{10.3}\]
where P is the power incident on the thin layer of sample and \(\alpha\) is a proportionality constant. Integrating the left side of Equation \ref{10.3} over the sample’s full thickness
\[-\int_{P=P_0}^{P=P_t} \frac{d P}{P}=\alpha C \int_{x=0}^{x=b} d x \nonumber\]
\[\ln \frac{P_{0}}{P_T}=\alpha b C \nonumber\]
converting from ln to log, and substituting into Equation \ref{10.2}, gives
where a is the analyte’s absorptivity with units of cm–1 conc–1. If we express the concentration using molarity, then we replace a with the molar absorptivity, \(\varepsilon\), which has units of cm–1 M–1.
\[A=\varepsilon b C \label{10.5}\]
The absorptivity and the molar absorptivity are proportional to the probability that the analyte absorbs a photon of a given energy. As a result, values for both a and \(\varepsilon\) depend on the wavelength of the absorbed photon.
A \(5.00 \times 10^{-4}\) M solution of analyte is placed in a sample cell that has a pathlength of 1.00 cm. At a wavelength of 490 nm, the solution’s absorbance is 0.338. What is the analyte’s molar absorptivity at this wavelength?
Solution
Solving Equation \ref{10.5} for \(\epsilon\) and making appropriate substitutions gives
\[\varepsilon=\frac{A}{b C}=\frac{0.338}{(1.00 \ \mathrm{cm})\left(5.00 \times 10^{-4} \ \mathrm{M}\right)}=676 \ \mathrm{cm}^{-1} \ \mathrm{M}^{-1} \nonumber\]
A solution of the analyte from Example 10.2.2 has an absorbance of 0.228 in a 1.00-cm sample cell. What is the analyte’s concentration?
- Answer
-
Making appropriate substitutions into Beer’s law
\[A=0.228=\varepsilon b C=\left(676 \ \mathrm{M}^{-1} \ \mathrm{cm}^{-1}\right)(1 \ \mathrm{cm}) C \nonumber\]
and solving for C gives a concentration of \(3.37 \times 10^{-4}\) M.
Equation \ref{10.4} and Equation \ref{10.5}, which establish the linear relationship between absorbance and concentration, are known as Beer’s law. Calibration curves based on Beer’s law are common in quantitative analyses.
As is often the case, the formulation of a law is more complicated than its name suggests. This is the case, for example, with Beer’s law, which also is known as the Beer-Lambert law or the Beer-Lambert-Bouguer law. Pierre Bouguer, in 1729, and Johann Lambert, in 1760, noted that the transmittance of light decreases exponentially with an increase in the sample’s thickness.
\[T \propto e^{-b} \nonumber\]
Later, in 1852, August Beer noted that the transmittance of light decreases exponentially as the concentration of the absorbing species increases.
\[T \propto e^{-C} \nonumber\]
Together, and when written in terms of absorbance instead of transmittance, these two relationships make up what we know as Beer’s law.
Beer's Law and Multicomponent Samples
We can extend Beer’s law to a sample that contains several absorbing components. If there are no interactions between the components, then the individual absorbances, Ai, are additive. For a two-component mixture of analyte’s X and Y, the total absorbance, Atot, is
\[A_{tot}=A_{X}+A_{Y}=\varepsilon_{X} b C_{X}+\varepsilon_{Y} b C_{Y} \nonumber\]
Generalizing, the absorbance for a mixture of n components, Amix, is
\[A_{m i x}=\sum_{i=1}^{n} A_{i}=\sum_{i=1}^{n} \varepsilon_{i} b C_{i} \label{10.6}\]
Limitations to Beer's Law
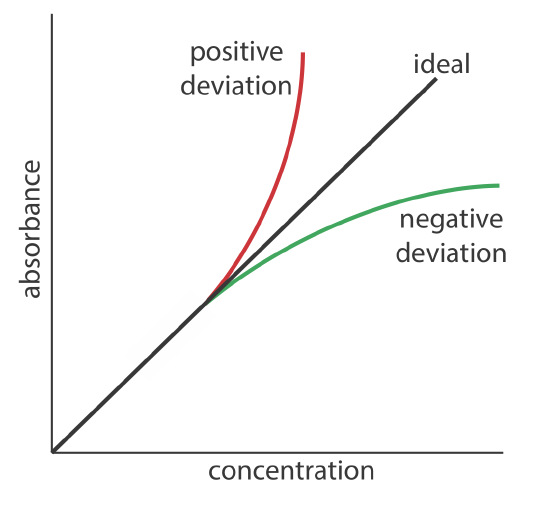
Beer’s law suggests that a plot of absorbance vs. concentration—we will call this a Beer’s law plot—is a straight line with a y-intercept of zero and a slope of ab or \(\varepsilon b\). In some cases a Beer’s law plot deviates from this ideal behavior (see Figure 10.2.9 ), and such deviations from linearity are divided into three categories: fundamental, chemical, and instrumental.
Fundamental Limitations to Beer's Law
Beer’s law is a limiting law that is valid only for low concentrations of analyte. There are two contributions to this fundamental limitation to Beer’s law. At higher concentrations the individual particles of analyte no longer are independent of each other. The resulting interaction between particles of analyte may change the analyte’s absorptivity. A second contribution is that an analyte’s absorptivity depends on the solution’s refractive index. Because a solution’s refractive index varies with the analyte’s concentration, values of a and \(\varepsilon\) may change. For sufficiently low concentrations of analyte, the refractive index essentially is constant and a Beer’s law plot is linear.
Chemical Limitations to Beer's Law
A chemical deviation from Beer’s law may occur if the analyte is involved in an equilibrium reaction. Consider, for example, the weak acid, HA. To construct a Beer’s law plot we prepare a series of standard solutions—each of which contains a known total concentration of HA—and then measure each solution’s absorbance at the same wavelength. Because HA is a weak acid, it is in equilibrium with its conjugate weak base, A–.
In the equations that follow, the conjugate weak base A– is written as A as it is easy to mistake the symbol for anionic charge as a minus sign.
\[\mathrm{HA}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q) \nonumber\]
If both HA and A– absorb at the selected wavelength, then Beer’s law is
\[A=\varepsilon_{\mathrm{HA}} b C_{\mathrm{HA}}+\varepsilon_{\mathrm{A}} b C_{\mathrm{A}} \label{10.7}\]
Because the weak acid’s total concentration, Ctotal, is
\[C_{\mathrm{total}}=C_{\mathrm{HA}}+C_{\mathrm{A}} \nonumber\]
we can write the concentrations of HA and A– as
\[C_{\mathrm{HA}}=\alpha_{\mathrm{HA}} C_{\mathrm{total}} \label{10.8}\]
\[C_{\text{A}} = (1 - \alpha_\text{HA})C_\text{total} \label{10.9}\]
where \(\alpha_\text{HA}\) is the fraction of weak acid present as HA. Substituting Equation \ref{10.8} and Equation \ref{10.9} into Equation \ref{10.7} and rearranging, gives
\[A=\left(\varepsilon_{\mathrm{HA}} \alpha_{\mathrm{HA}}+\varepsilon_{\mathrm{A}}-\varepsilon_{\mathrm{A}} \alpha_{\mathrm{A}}\right) b C_{\mathrm{total}} \label{10.10}\]
To obtain a linear Beer’s law plot, we must satisfy one of two conditions. If \(\varepsilon_\text{HA}\) and \(\varepsilon_{\text{A}}\) have the same value at the selected wavelength, then Equation \ref{10.10} simplifies to
\[A = \varepsilon_{\text{A}}bC_\text{total} = \varepsilon_\text{HA}bC_\text{total} \nonumber\]
Alternatively, if \(\alpha_\text{HA}\) has the same value for all standard solutions, then each term within the parentheses of Equation \ref{10.10} is constant—which we replace with k—and a linear calibration curve is obtained at any wavelength.
\[A=k b C_{\mathrm{total}} \nonumber\]
Because HA is a weak acid, the value of \(\alpha_\text{HA}\) varies with pH. To hold \(\alpha_\text{HA}\) constant we buffer each standard solution to the same pH. Depending on the relative values of \(\alpha_\text{HA}\) and \(\alpha_{\text{A}}\), the calibration curve has a positive or a negative deviation from Beer’s law if we do not buffer the standards to the same pH.
Instrumental Limitations to Beer's Law
There are two principal instrumental limitations to Beer’s law. The first limitation is that Beer’s law assumes that radiation reaching the sample is of a single wavelength—that is, it assumes a purely monochromatic source of radiation. As shown in Figure 10.1.10, even the best wavelength selector passes radiation with a small, but finite effective bandwidth. Polychromatic radiation always gives a negative deviation from Beer’s law, but the effect is smaller if the value of \(\varepsilon\) essentially is constant over the wavelength range passed by the wavelength selector. For this reason, as shown in Figure 10.2.10 , it is better to make absorbance measurements at the top of a broad absorption peak. In addition, the deviation from Beer’s law is less serious if the source’s effective bandwidth is less than one-tenth of the absorbing species’ natural bandwidth [(a) Strong, F. C., III Anal. Chem. 1984, 56, 16A–34A; Gilbert, D. D. J. Chem. Educ. 1991, 68, A278–A281]. When measurements must be made on a slope, linearity is improved by using a narrower effective bandwidth.

Stray radiation is the second contribution to instrumental deviations from Beer’s law. Stray radiation arises from imperfections in the wavelength selector that allow light to enter the instrument and to reach the detector without passing through the sample. Stray radiation adds an additional contribution, Pstray, to the radiant power that reaches the detector; thus
\[A=-\log \frac{P_{\mathrm{T}}+P_{\text { stray }}}{P_{0}+P_{\text { stray }}} \nonumber\]
For a small concentration of analyte, Pstray is significantly smaller than P0 and PT, and the absorbance is unaffected by the stray radiation. For higher concentrations of analyte, less light passes through the sample and PT and Pstray become similar in magnitude. This results is an absorbance that is smaller than expected, and a negative deviation from Beer’s law.


