7.7: Liquid-Liquid Extractions
- Page ID
- 220719
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A liquid–liquid extraction is an important separation technique for environmental, clinical, and industrial laboratories. A standard environmental analytical method illustrates the importance of liquid–liquid extractions. Municipal water departments routinely monitor public water supplies for trihalomethanes (CHCl3, CHBrCl2, CHBr2Cl, and CHBr3) because they are known or suspected carcinogens. Before their analysis by gas chromatography, trihalomethanes are separated from their aqueous matrix using a liquid–liquid extraction with pentane [“The Analysis of Trihalomethanes in Drinking Water by Liquid Extraction,”EPAMethod501.2 (EPA 500-Series, November 1979)].
The Environmental Protection Agency (EPA) also publishes two additional methods for trihalomethanes. Method 501.1 and Method 501.3 use a purge-and-trap to collect the trihalomethanes prior to a gas chromatographic analysis with a halide-specific detector (Method 501.1) or a mass spectrometer as the detector (Method 501.3). You will find more details about gas chromatography, including detectors, in Chapter 12.
In a simple liquid–liquid extraction the solute partitions itself between two immiscible phases. One phase usually is an aqueous solvent and the other phase is an organic solvent, such as the pentane used to extract trihalomethanes from water. Because the phases are immiscible they form two layers, with the denser phase on the bottom. The solute initially is present in one of the two phases; after the extraction it is present in both phases. Extraction efficiency—that is, the percentage of solute that moves from one phase to the other—is determined by the equilibrium constant for the solute’s partitioning between the phases and any other side reactions that involve the solute. Examples of other reactions that affect extraction efficiency include acid–base reactions and complexation reactions.
Partition Coefficients and Distribution Ratios
As we learned earlier in this chapter, a solute’s partitioning between two phases is described by a partition coefficient, KD. If we extract a solute from an aqueous phase into an organic phase
\[S_{a q} \rightleftharpoons S_{o r g} \nonumber\]
then the partition coefficient is
\[K_{\mathrm{D}}=\frac{\left[S_{org}\right]}{\left[S_{a q}\right]} \nonumber\]
A large value for KD indicates that extraction of solute into the organic phase is favorable.
To evaluate an extraction’s efficiency we must consider the solute’s total concentration in each phase, which we define as a distribution ratio, D.
\[D=\frac{\left[S_{o r g}\right]_{\text { total }}}{\left[S_{a q}\right]_{\text { total }}} \nonumber\]
The partition coefficient and the distribution ratio are identical if the solute has only one chemical form in each phase; however, if the solute exists in more than one chemical form in either phase, then KD and D usually have different values. For example, if the solute exists in two forms in the aqueous phase, A and B, only one of which, A, partitions between the two phases, then
\[D=\frac{\left[S_{o r g}\right]_{A}}{\left[S_{a q}\right]_{A}+\left[S_{a q}\right]_{B}} \leq K_{\mathrm{D}}=\frac{\left[S_{o r g}\right]_{A}}{\left[S_{a q}\right]_{A}} \nonumber\]
This distinction between KD and D is important. The partition coefficient is a thermodynamic equilibrium constant and has a fixed value for the solute’s partitioning between the two phases. The distribution ratio’s value, however, changes with solution conditions if the relative amounts of A and B change. If we know the solute’s equilibrium reactions within each phase and between the two phases, we can derive an algebraic relationship between KD and D.
Liquid-Liquid Extraction With No Secondary Reactions
In a simple liquid–liquid extraction, the only reaction that affects the extraction efficiency is the solute’s partitioning between the two phases (Figure \(\PageIndex{1}\)).
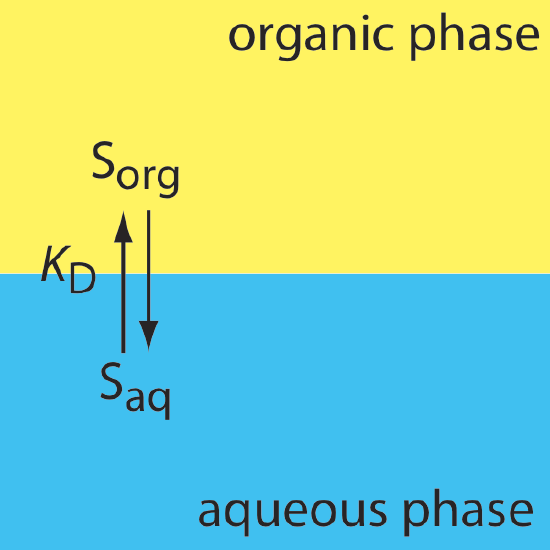
In this case the distribution ratio and the partition coefficient are equal.
\[D=\frac{\left[S_{o r g}\right]_{\text { total }}}{\left[S_{aq}\right]_{\text { total }}} = K_\text{D} = \frac {[S_{org}]} {[S_{aq}]} \label{7.1}\]
Let’s assume the solute initially is present in the aqueous phase and that we wish to extract it into the organic phase. A conservation of mass requires that the moles of solute initially present in the aqueous phase equal the combined moles of solute in the aqueous phase and the organic phase after the extraction.
\[\left(\operatorname{mol} \ S_{a q}\right)_{0}=\left(\operatorname{mol} \ S_{a q}\right)_{1}+\left(\operatorname{mol} \ S_{org}\right)_{1} \label{7.2}\]
where the subscripts indicate the extraction number with 0 representing the system before the extraction and 1 the system following the first extraction. After the extraction, the solute’s concentration in the aqueous phase is
\[\left[S_{a q}\right]_{1}=\frac{\left(\operatorname{mol} \ S_{a q}\right)_{1}}{V_{a q}} \label{7.3}\]
and its concentration in the organic phase is
\[\left[S_{o r g}\right]_{1}=\frac{\left(\operatorname{mol} \ S_{o r g}\right)_{1}}{V_{o r g}} \label{7.4}\]
where Vaq and Vorg are the volumes of the aqueous phase and the organic phase. Solving equation \ref{7.2} for (mol Sorg)1 and substituting into equation \ref{7.4} leave us with
\[\left[S_{o r g}\right]_{1} = \frac{\left(\operatorname{mol} \ S_{a q}\right)_{0}-\left(\operatorname{mol} \ S_{a q}\right)_{1}}{V_{o r g}} \label{7.5}\]
Substituting equation \ref{7.3} and equation \ref{7.5} into equation \ref{7.1} gives
\[D = \frac {\frac {(\text{mol }S_{aq})_0-(\text{mol }S_{aq})_1} {V_{org}}} {\frac {(\text{mol }S_{aq})_1} {V_{aq}}} = \frac{\left(\operatorname{mol} \ S_{a q}\right)_{0} \times V_{a q}-\left(\operatorname{mol} \ S_{a q}\right)_{1} \times V_{a q}}{\left(\operatorname{mol} \ S_{a q}\right)_{1} \times V_{o r g}} \nonumber\]
Rearranging and solving for the fraction of solute that remains in the aqueous phase after one extraction, (qaq)1, gives
\[\left(q_{aq}\right)_{1} = \frac{\left(\operatorname{mol} \ S_{aq}\right)_{1}}{\left(\operatorname{mol} \ S_{a q}\right)_{0}} = \frac{V_{aq}}{D V_{o r g}+V_{a q}} \label{7.6}\]
The fraction present in the organic phase after one extraction, (qorg)1, is
\[\left(q_{o r g}\right)_{1}=\frac{\left(\operatorname{mol} S_{o r g}\right)_{1}}{\left(\operatorname{mol} S_{a q}\right)_{0}}=1-\left(q_{a q}\right)_{1}=\frac{D V_{o r g}}{D V_{o r g}+V_{a q}} \nonumber\]
Example \(\PageIndex{1}\) shows how we can use equation \ref{7.6} to calculate the efficiency of a simple liquid-liquid extraction.
A solute has a KD between water and chloroform of 5.00. Suppose we extract a 50.00-mL sample of a 0.050 M aqueous solution of the solute using 15.00 mL of chloroform. (a) What is the separation’s extraction efficiency? (b) What volume of chloroform do we need if we wish to extract 99.9% of the solute?
Solution
For a simple liquid–liquid extraction the distribution ratio, D, and the partition coefficient, KD, are identical.
(a) The fraction of solute that remains in the aqueous phase after the extraction is given by equation \ref{7.6}.
\[\left(q_{aq}\right)_{1}=\frac{V_{a q}}{D V_{org}+V_{a q}}=\frac{50.00 \ \mathrm{mL}}{(5.00)(15.00 \ \mathrm{mL})+50.00 \ \mathrm{mL}}=0.400 \nonumber\]
The fraction of solute in the organic phase is 1–0.400, or 0.600. Extraction efficiency is the percentage of solute that moves into the extracting phase; thus, the extraction efficiency is 60.0%.
(b) To extract 99.9% of the solute (qaq)1 must be 0.001. Solving equation \ref{7.6} for Vorg, and making appropriate substitutions for (qaq)1 and Vaq gives
\[V_{o r g}=\frac{V_{a q}-\left(q_{a q}\right)_{1} V_{a q}}{\left(q_{a q}\right)_{1} D}=\frac{50.00 \ \mathrm{mL}-(0.001)(50.00 \ \mathrm{mL})}{(0.001)(5.00 \ \mathrm{mL})}=999 \ \mathrm{mL} \nonumber\]
This is large volume of chloroform. Clearly, a single extraction is not reasonable under these conditions.
In Example \(\PageIndex{1}\), a single extraction provides an extraction efficiency of only 60%. If we carry out a second extraction, the fraction of solute remaining in the aqueous phase, (qaq)2, is
\[\left(q_{a q}\right)_{2}=\frac{\left(\operatorname{mol} \ S_{a q}\right)_{2}}{\left(\operatorname{mol} \ S_{a q}\right)_{1}}=\frac{V_{a q}}{D V_{org}+V_{a q}} \nonumber\]
If Vaq and Vorg are the same for both extractions, then the cumulative fraction of solute that remains in the aqueous layer after two extractions, (Qaq)2, is the product of (qaq)1 and (qaq)2, or
\[\left(Q_{aq}\right)_{2}=\frac{\left(\operatorname{mol} \ S_{aq}\right)_{2}}{\left(\operatorname{mol} \ S_{aq}\right)_{0}}=\left(q_{a q}\right)_{1} \times\left(q_{a q}\right)_{2}=\left(\frac{V_{a q}}{D V_{o r g}+V_{a q}}\right)^{2} \nonumber\]
In general, for a series of n identical extractions, the fraction of analyte that remains in the aqueous phase after the last extraction is
\[\left(Q_{a q}\right)_{n}=\left(\frac{V_{a q}}{D V_{o r g}+V_{a q}}\right)^{n} \label{7.7}\]
For the extraction described in Example \(\PageIndex{1}\), determine (a) the extraction efficiency for two identical extractions and for three identical extractions; and (b) the number of extractions required to ensure that we extract 99.9% of the solute.
Solution
(a) The fraction of solute remaining in the aqueous phase after two extractions and three extractions is
\[\left(Q_{aq}\right)_{2}=\left(\frac{50.00 \ \mathrm{mL}}{(5.00)(15.00 \ \mathrm{mL})+50.00 \ \mathrm{mL}}\right)^{2}=0.160 \nonumber\]
\[\left(Q_{a q}\right)_{3}=\left(\frac{50.0 \ \mathrm{mL}}{(5.00)(15.00 \ \mathrm{mL})+50.00 \ \mathrm{mL}}\right)^{3}=0.0640 \nonumber\]
The extraction efficiencies are 84.0% for two extractions and 93.6% for three extractions.
(b) To determine the minimum number of extractions for an efficiency of 99.9%, we set (Qaq)n to 0.001 and solve for n using equation \ref{7.7}.
\[0.001=\left(\frac{50.00 \ \mathrm{mL}}{(5.00)(15.00 \ \mathrm{mL})+50.00 \ \mathrm{mL}}\right)^{n}=(0.400)^{n} \nonumber\]
Taking the log of both sides and solving for n
\[\begin{aligned} \log (0.001) &=n \log (0.400) \\ n &=7.54 \end{aligned} \nonumber\]
we find that a minimum of eight extractions is necessary.
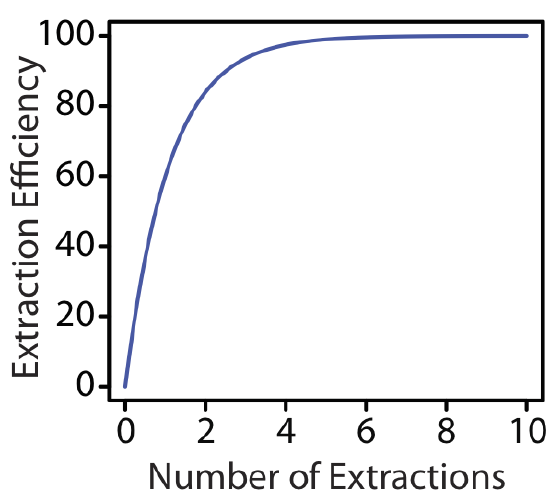
The last two examples provide us with an important observation—for any extraction efficiency, we need less solvent if we complete several extractions using smaller portions of solvent instead of one extraction using a larger volume of solvent. For the conditions in Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\), an extraction efficiency of 99.9% requires one extraction with 9990 mL of chloroform, or 120 mL when using eight 15-mL portions of chloroform. Although extraction efficiency increases dramatically with the first few multiple, the effect diminishes quickly as we increase the number of extractions (Figure \(\PageIndex{2}\)). In most cases there is little improvement in extraction efficiency after five or six extractions. For the conditions in Example \(\PageIndex{2}\), we reach an extraction efficiency of 99% after five extractions and need three additional extractions to obtain the extra 0.9% increase in extraction efficiency.
To plan a liquid–liquid extraction we need to know the solute’s distribution ratio between the two phases. One approach is to carry out the extraction on a solution that contains a known amount of solute. After the extraction, we isolate the organic phase and allow it to evaporate, leaving behind the solute. In one such experiment, 1.235 g of a solute with a molar mass of 117.3 g/mol is dissolved in 10.00 mL of water. After extracting with 5.00 mL of toluene, 0.889 g of the solute is recovered in the organic phase. (a) What is the solute’s distribution ratio between water and toluene? (b) If we extract 20.00 mL of an aqueous solution that contains the solute using 10.00 mL of toluene, what is the extraction efficiency? (c) How many extractions will we need to recover 99.9% of the solute?
- Answer
-
(a) The solute’s distribution ratio between water and toluene is
\[D=\frac{\left[S_{o r g}\right]}{\left[S_{a q}\right]}=\frac{0.889 \ \mathrm{g} \times \frac{1 \ \mathrm{mol}}{117.3 \ \mathrm{g}} \times \frac{1}{0.00500 \ \mathrm{L}}}{(1.235 \ \mathrm{g}-0.889 \ \mathrm{g}) \times \frac{1 \ \mathrm{mol}}{117.3 \ \mathrm{g}} \times \frac{1}{0.01000 \ \mathrm{L}}}=5.14 \nonumber\]
(b) The fraction of solute remaining in the aqueous phase after one extraction is
\[\left(q_{a q}\right)_{1}=\frac{V_{a q}}{D V_{org}+V_{a q}}=\frac{20.00 \ \mathrm{mL}}{(5.14)(10.00 \ \mathrm{mL})+20.00 \ \mathrm{mL}}=0.280 \nonumber\]
The extraction efficiency, therefore, is 72.0%.
(c) To extract 99.9% of the solute requires
\[\left(Q_{aq}\right)_{n}=0.001=\left(\frac{20.00 \ \mathrm{mL}}{(5.14)(10.00 \ \mathrm{mL})+20.00 \ \mathrm{mL}}\right)^{n}=(0.280)^{n} \nonumber\]
\[\begin{aligned} \log (0.001) &=n \log (0.280) \\ n &=5.4 \end{aligned} \nonumber\]
a minimum of six extractions.
Liquid-Liquid Extractions Involving Acid-Base Equilibria
As we see in equation \ref{7.1}, in a simple liquid–liquid extraction the distribution ratio and the partition coefficient are identical. As a result, the distribution ratio does not depend on the composition of the aqueous phase or the organic phase. A change in the pH of the aqueous phase, for example, will not affect the solute’s extraction efficiency when KD and D have the same value.
If the solute participates in one or more additional equilibrium reactions within a phase, then the distribution ratio and the partition coefficient may not be the same. For example, Figure \(\PageIndex{3}\) shows the equilibrium reactions that affect the extraction of the weak acid, HA, by an organic phase in which ionic species are not soluble.
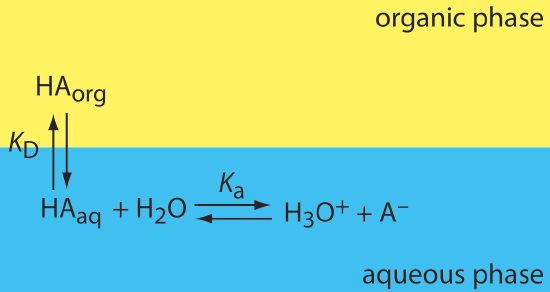
In this case the partition coefficient and the distribution ratio are
\[K_{\mathrm{D}}=\frac{\left[\mathrm{HA}_{org}\right]}{\left[\mathrm{HA}_{a q}\right]} \label{7.8}\]
\[D=\frac{\left[\mathrm{HA}_{org}\right]_{\text { total }}}{\left[\mathrm{HA}_{a q}\right]_{\text { total }}} =\frac{\left[\mathrm{HA}_{org}\right]}{\left[\mathrm{HA}_{a q}\right]+\left[\mathrm{A}_{a q}^{-}\right]} \label{7.9}\]
Because the position of an acid–base equilibrium depends on pH, the distribution ratio, D, is pH-dependent. To derive an equation for D that shows this dependence, we begin with the acid dissociation constant for HA.
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}_{\mathrm{aq}}^{+}\right]\left[\mathrm{A}_{\mathrm{aq}}^{-}\right]}{\left[\mathrm{HA}_{\mathrm{aq}}\right]} \label{7.10}\]
Solving equation \ref{7.10} for the concentration of A– in the aqueous phase
\[\left[\mathrm{A}_{a q}^{-}\right]=\frac{K_{\mathrm{a}} \times\left[\mathrm{HA}_{a q}\right]}{\left[\mathrm{H}_{3} \mathrm{O}_{a q}^{+}\right]} \nonumber\]
and substituting into equation \ref{7.9} gives
\[D = \frac {[\text{HA}_{org}]} {[\text{HA}_{aq}] + \frac {K_a \times [\text{HA}_{aq}]}{[\text{H}_3\text{O}_{aq}^+]}} \nonumber\]
Factoring [HAaq] from the denominator, replacing [HAorg]/[HAaq] with KD (equation \ref{7.8}), and simplifying leaves us with the following relationship between the distribution ratio, D, and the pH of the aqueous solution.
\[D=\frac{K_{\mathrm{D}}\left[\mathrm{H}_{3} \mathrm{O}_{aq}^{+}\right]}{\left[\mathrm{H}_{3} \mathrm{O}_{aq}^{+}\right]+K_{a}} \label{7.11}\]
An acidic solute, HA, has a Ka of \(1.00 \times 10^{-5}\) and a KD between water and hexane of 3.00. Calculate the extraction efficiency if we extract a 50.00 mL sample of a 0.025 M aqueous solution of HA, buffered to a pH of 3.00, with 50.00 mL of hexane. Repeat for pH levels of 5.00 and 7.00.
Solution
When the pH is 3.00, [\(\text{H}_3\text{O}_{aq}^+\)] is \(1.0 \times 10^{-3}\) and the distribution ratio is
\[D=\frac{(3.00)\left(1.0 \times 10^{-3}\right)}{1.0 \times 10^{-3}+1.00 \times 10^{-5}}=2.97 \nonumber\]
The fraction of solute that remains in the aqueous phase is
\[\left(Q_{aq}\right)_{1}=\frac{50.00 \ \mathrm{mL}}{(2.97)(50.00 \ \mathrm{mL})+50.00 \ \mathrm{mL}}=0.252 \nonumber\]
The extraction efficiency, therefore, is almost 75%. The same calculation at a pH of 5.00 gives the extraction efficiency as 60%. At a pH of 7.00 the extraction efficiency is just 3% .
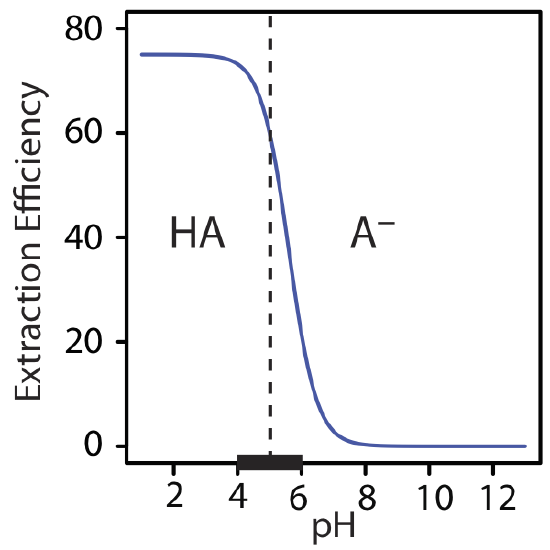
The extraction efficiency in Example \(\PageIndex{3}\) is greater at more acidic pH levels because HA is the solute’s predominate form in the aqueous phase. At a more basic pH, where A– is the solute’s predominate form, the extraction efficiency is smaller. A graph of extraction efficiency versus pH is shown in Figure \(\PageIndex{4}\). Note that extraction efficiency essentially is independent of pH for pH levels more acidic than the HA’s pKa, and that it is essentially zero for pH levels more basic than HA’s pKa. The greatest change in extraction efficiency occurs at pH levels where both HA and A– are predominate species. The ladder diagram for HA along the graph’s x-axis helps illustrate this effect.
The liquid–liquid extraction of the weak base B is governed by the following equilibrium reactions:
\[\begin{array}{c}{\mathrm{B}(a q) \rightleftharpoons \mathrm{B}(org) \quad K_{D}=5.00} \\ {\mathrm{B}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{HB}^{+}(a q) \quad K_{b}=1.0 \times 10^{-4}}\end{array} \nonumber\]
Derive an equation for the distribution ratio, D, and calculate the extraction efficiency if 25.0 mL of a 0.025 M solution of B, buffered to a pH of 9.00, is extracted with 50.0 mL of the organic solvent.
- Answer
-
Because the weak base exists in two forms, only one of which extracts into the organic phase, the partition coefficient, KD, and the distribution ratio, D, are not identical.
\[K_{\mathrm{D}}=\frac{\left[\mathrm{B}_{org}\right]}{\left[\mathrm{B}_{aq}\right]} \nonumber\]
\[D = \frac {[\text{B}_{org}]} {[\text{B}_{aq}]} = \frac {[\text{B}_{org}]} {[\text{B}_{aq}] + [\text{HB}_{aq}^+]} \nonumber\]
Using the Kb expression for the weak base
\[K_{\mathrm{b}}=\frac{\left[\mathrm{OH}_{a q}^{-}\right]\left[\mathrm{HB}_{a q}^{+}\right]}{\left[\mathrm{B}_{a q}\right]} \nonumber\]
we solve for the concentration of HB+ and substitute back into the equation for D, obtaining
\[D = \frac {[\text{B}_{org}]} {[\text{B}_{aq}] + \frac {K_b \times [\text{B}_{aq}]} {[\text{OH}_{aq}^-]}} = \frac {[\text{B}_{org}]} {[\text{B}_{aq}]\left(1+\frac {K_b} {[\text{OH}_{aq}^+]} \right)} =\frac{K_{D}\left[\mathrm{OH}_{a q}^{-}\right]}{\left[\mathrm{OH}_{a q}^{-}\right]+K_{\mathrm{b}}} \nonumber\]
At a pH of 9.0, the [OH–] is \(1 \times 10^{-5}\) M and the distribution ratio has a value of
\[D=\frac{K_{D}\left[\mathrm{OH}_{a q}^{-}\right]}{\left[\mathrm{OH}_{aq}^{-}\right]+K_{\mathrm{b}}}=\frac{(5.00)\left(1.0 \times 10^{-5}\right)}{1.0 \times 10^{-5}+1.0 \times 10^{-4}}=0.455 \nonumber\]
After one extraction, the fraction of B remaining in the aqueous phase is
\[\left(q_{aq}\right)_{1}=\frac{25.00 \ \mathrm{mL}}{(0.455)(50.00 \ \mathrm{mL})+25.00 \ \mathrm{mL}}=0.524 \nonumber\]
The extraction efficiency, therefore, is 47.6%. At a pH of 9, most of the weak base is present as HB+, which explains why the overall extraction efficiency is so poor.
Liquid-Liquid Extraction of a Metal-Ligand Complex
One important application of a liquid–liquid extraction is the selective extraction of metal ions using an organic ligand. Unfortunately, many organic ligands are not very soluble in water or undergo hydrolysis or oxidation reactions in aqueous solutions. For these reasons the ligand is added to the organic solvent instead of the aqueous phase. Figure \(\PageIndex{5}\) shows the relevant equilibrium reactions (and equilibrium constants) for the extraction of Mn+ by the ligand HL, including the ligand’s extraction into the aqueous phase (KD,HL), the ligand’s acid dissociation reaction (Ka), the formation of the metal–ligand complex (\(\beta_n\)), and the complex’s extraction into the organic phase (KD,c).
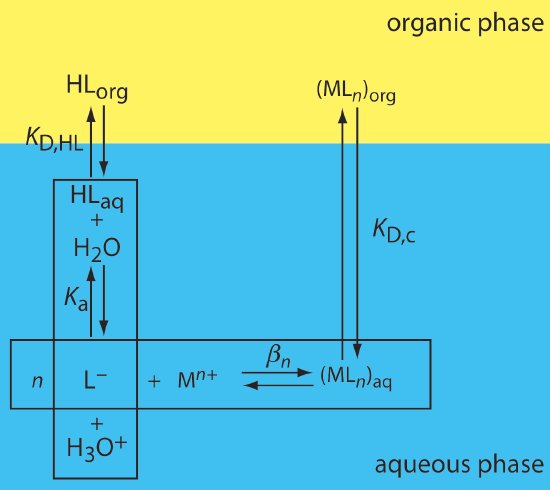
If the ligand’s concentration is much greater than the metal ion’s concentration, then the distribution ratio is
\[D=\frac{\beta_{n} K_{\mathrm{D}, c}\left(K_{a}\right)^{n}\left(C_{\mathrm{HL}}\right)^{n}}{\left(K_{\mathrm{D}, \mathrm{HL}}\right)^{n}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{n}+\beta_{n}\left(K_{\mathrm{a}}\right)^{n}\left(C_{\mathrm{HL}}\right)^{n}} \label{7.12}\]
where CHL is the ligand’s initial concentration in the organic phase. As shown in Example \(\PageIndex{4}\), the extraction efficiency for metal ions shows a marked pH dependency.
A liquid–liquid extraction of the divalent metal ion, M2+, uses the scheme outlined in Figure \(\PageIndex{5}\). The partition coefficients for the ligand, KD,HL, and for the metal–ligand complex, KD,c, are \(1.0 \times 10^4\) and \(7.0 \times 10^4\), respectively. The ligand’s acid dissociation constant, Ka, is \(5.0 \times 10^{-5}\), and the formation constant for the metal–ligand complex, \(\beta_2\), is \(2.5 \times 10^{16}\). What is the extraction efficiency if we extract 100.0 mL of a \(1.0 \times 10^{-6}\) M aqueous solution of M2+, buffered to a pH of 1.00, with 10.00 mL of an organic solvent that is 0.1 mM in the chelating agent? Repeat the calculation at a pH of 3.00.
Solution
When the pH is 1.00 the distribution ratio is
\[D=\frac{\left(2.5 \times 10^{16}\right)\left(7.0 \times 10^{4}\right)\left(5.0 \times 10^{-5}\right)^{2}\left(1.0 \times 10^{-4}\right)^{2}}{\left(1.0 \times 10^{4}\right)^{2}(0.10)^{2}+\left(2.5 \times 10^{16}\right)\left(5.0 \times 10^{-5}\right)^{2}\left(1.0 \times 10^{-4}\right)^{2}} \nonumber\]
or a D of 0.0438. The fraction of metal ion that remains in the aqueous phase is
\[\left(Q_{aq}\right)_{1}=\frac{100.0 \ \mathrm{mL}}{(0.0438)(10.00 \ \mathrm{mL})+100.0 \ \mathrm{mL}}=0.996 \nonumber\]
At a pH of 1.00, we extract only 0.40% of the metal into the organic phase. Changing the pH to 3.00, however, increases the extraction efficiency to 97.8%. Figure \(\PageIndex{6}\) shows how the pH of the aqueous phase affects the extraction efficiency for M2+.
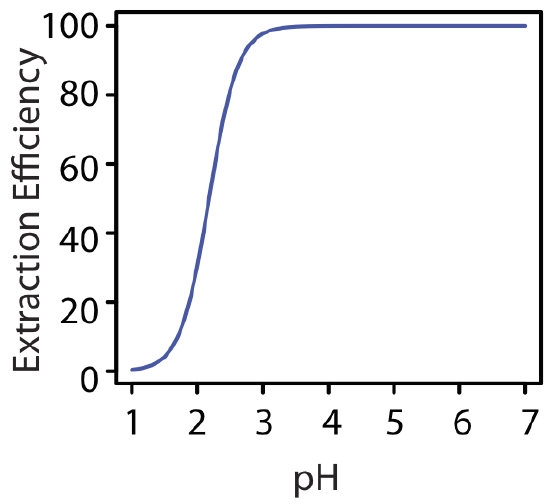
One advantage of using a ligand to extract a metal ion is the high degree of selectivity that it brings to a liquid–liquid extraction. As seen in Figure \(\PageIndex{6}\), a divalent metal ion’s extraction efficiency increases from approximately 0% to 100% over a range of 2 pH units. Because a ligand’s ability to form a metal–ligand complex varies substantially from metal ion to metal ion, significant selectivity is possible if we carefully control the pH. Table \(\PageIndex{1}\) shows the minimum pH for extracting 99% of a metal ion from an aqueous solution using an equal volume of 4 mM dithizone in CCl4.
| metal ion | minimum pH |
|---|---|
| Hg2+ | –8.7 |
| Ag+ | –1.7 |
| Cu2+ | –0.8 |
| Bi3+ | 0.9 |
| Zn2+ | 2.3 |
| Cd2+ | 3.6 |
| Co2+ | 3.6 |
| Pb2+ | 4.1 |
| Ni2+ | 6.0 |
| Tl+ | 8.7 |
Using Table \(\PageIndex{1}\), explain how we can separate the metal ions in an aqueous mixture of Cu2+, Cd2+, and Ni2+ by extracting with an equal volume of dithizone in CCl4.
Solution
From Table \(\PageIndex{1}\), a quantitative separation of Cu2+ from Cd2+ and from Ni2+ is possible if we acidify the aqueous phase to a pH of less than 1. This pH is greater than the minimum pH for extracting Cu2+ and significantly less than the minimum pH for extracting either Cd2+ or Ni2+. After the extraction of Cu2+ is complete, we shift the pH of the aqueous phase to 4.0, which allows us to extract Cd2+ while leaving Ni2+ in the aqueous phase.


