Raman: Theory
- Page ID
- 1850
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The phenomenon of Raman scattering of light was first postulated by Smekai in 1923 and first observed experimentally in 1928 by Raman and Krishnan. Raman scattering is most easily seen as the change in frequency for a small percentage of the intensity in a monochromatic beam as the result of coupling between the incident radiation and vibrational energy levels of molecules. A vibrational mode will be Raman active only when it changes the polariazbility of the molecule.
Introduction
When monochromatic radiation with a wavenumber \(\tilde{\nu}_{0}\) is incident on systems, most of it is transmitted without change, but, in addition, some scattering of the radiation occurs. If the frequency content of the scattered radiation is analyzed, there will be observed to be present not only the wavenumber \(\tilde{\nu}_{0}\) associated with the incident radiation but also, in general, pairs of new wavenumbers of the type \(\tilde{\nu} ^{'}=\tilde{\nu} _{0}+\tilde{\nu} _{M}\). In molecular systems, the wavenumbers \(\tilde{\nu}_{M}\) are found to lie principally in the ranges associated with transitions between rotational, vibrational, and electronic levels.
Such scattering of radiation with change of wavenumber is called Raman Scattering, after the Indian scientist C. V. Raman who, with K. S. Krishnan, first observed this phenomenon in liquids in 1928. The effect had been predicted on theoretical grounds in 1923 by A. Smekal. Due to its very low scattering efficiency, Raman spectroscopy did not become popular until powerful laser systems were available after the 1960s. Now, Raman spectroscopy has become one of the most popular approaches to study the vibrational structures of molecules together with infrared spectrum.
The origin of the modified frequencies found in Raman scattering is explained in terms of energy transfer between the scattering system and the incident radiation. When a system interacts with radiation of wavenumber \(\tilde{\nu}_{0}\), it makes an upward transition from a lower energy level E1 to an upper energy level E2. It must then acquire the necessary energy, ΔE= E2- E1, from the incident radiation. The energy ΔE is expressed in terms of a wavenumber \(\tilde{\nu}_{M}\) associated with the two levels involved, where
\[ \Delta E=hc\tilde{\nu} _{M} \]
This energy requirement is regarded as being provided by the absorption of one photon of the incident radiation of energy \(hc\tilde{\nu}_{0}\) and the simultaneous emission of a photon of smaller energy \(hc\left (\tilde{\nu} _{0}-\tilde{\nu} _{M} \right )\), so that scattering of radiation of lower wavenumber, \(\tilde{\nu} _{0}-\tilde{\nu} _{M}\), occurs. Alternatively, the interaction of the radiation with the system may cause a downward transition from a higher energy level E2 to a lower energy level E1, in which case it makes available energy
\[ E_2-E_1=hc\tilde{\nu}_M \]
Again a photon of the incident radiation of energy \(hc\tilde{\nu}_{0}\) and the simultaneous emission of a photon of higher energy \(hc\left (\tilde{\nu} _{0}+\tilde{\nu} _{M} \right )\), so that scattering of radiation of higher wavenumber, \(\tilde{\nu} _{0}+\tilde{\nu} _{M}\), occurs.
In the case of Rayleigh scattering, although there is no resultant change in the energy state of the system, the system still participates directly in the scattering act, causing one photon of incident radiation \(hc\tilde{\nu}_{0}\) to be absorbed and a photon of the same energy to be emitted simultaneously, so that scattering of radiation of unchanged wavenumber, \(\tilde{\nu}_{0}\), occurs.
It is clear that, as far as wavenumber is concerned, a Raman band is to be characterized not by its absolute wavenumber, \(\tilde{\nu} ^{'}=\tilde{\nu} _{0}\pm\tilde{\nu} _{M}\), but by the magnitude of its wavenumber shift \(\tilde{\nu}_{M}\) from the incident wavenumber. Such wavenumber shifts are often referred to as Raman wavenumbers. Where it is necessary to distinguish Stokes and anti-Stokes Raman scattering we shall define \(\Delta\tilde{\nu}\) to be positive for Stokes scattering and negative for anti-Stokes scattering, that is \(\Delta \tilde{\nu} =\tilde{\nu}_{0} +\tilde{\nu}^{'}\) (see Fig. 1).
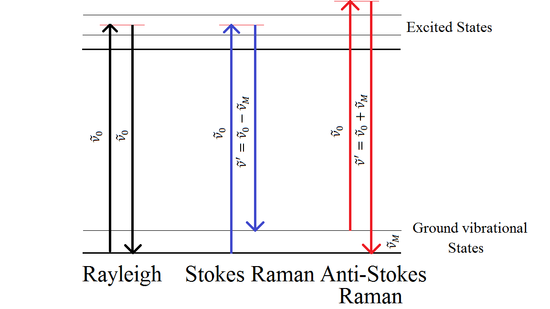
The intensity of anti-Stokes relative to Stokes Raman scattering decreases rapidly with increase in the wavenumber shift. This is because anti-Stokes Raman scattering involves transitions to a lower energy state from a populated higher energy states.
Classical theory
According to the classical theory of electromagnetic radiation, electric and magnetic fields oscillating at a given frequency are able to give out electromagnetic radiation of the same frequency. One could use electromagnetic radiation theory to explain light scattering phenomena.
For a majority of systems, only an induced electric dipole moment μ is taken into consideration. This dipole moment which is induced by the electric field E could be expressed by the power series
\[ \mathbf{\mu} =\mathbf{\mu}^{\left (1 \right )}+\mathbf{\mu}^{\left (2 \right )}+\mathbf{\mu}^{\left (3 \right )}+\cdots\]
where
\[ \mathbf{\mu}^{\left (1 \right )}=\mathbf{\alpha} \cdot \mathit{\mathbf{E}}\]
\( \mathbf{\mu}^{\left (2 \right )}=\frac{1}{2}\mathbf{\beta} \cdot \mathit{\mathbf{E}}\mathit{\mathbf{E}}\)
\( \mathbf{\mu}^{\left (3 \right )}=\frac{1}{6}\mathbf{\gamma } \cdot\mathit{\mathbf{E}}\mathit{\mathbf{E}}\mathit{\mathbf{E}}\)
α is termed the polarizability tensor. It is a second-rank tensor with all the components in the unit of CV-1m2. Typically, orders of magnitude for components in α, β, and γ are as follows, α, 10-40 CV-1m2; β, 10-50 CV-2m3; and γ, 10-61 CV-3m4. According to the values, the contributions of μ(2)and μ(3) are quite small unless electric field is very high. Since Rayleigh and Raman scattering are observed quite readily with very much lower electric field intensities, one may expect to explain Rayleigh and Raman scattering in terms of μ(1) only.
We shall now consider the interaction of a molecular system with the harmonically oscillating electric field in the frequency ω0. To make the explanation easily, we shall ignore the rotation but just consider the vibration part. It is to be expected that the polarizability will be a function of the nuclear coordinates. The variation of components in polarizability tensor with vibrational coordinates is expressed in a Taylor series
\( \alpha_{ij} =\left (\alpha_{ij} \right )_{0} +\sum_{k} \left (\frac{\partial \alpha_{ij} }{\partial Q_{k}} \right )_{0}Q_{k}+\frac{1}{2}\sum_{k,l}\left (\frac{\partial^2 \alpha_{ij}}{\partial Q_{k}\partial Q_{l}} \right )_{0}Q_{k}Q_{l}+\cdots \)
where (αij)0 is the αij value at the equilibrium configuration, Qk, Ql are normal coordinates of vibration at frequencies ωk, ωl. We shall make a harmonic approximation to neglect the terms which involve powers of Q higher than first. After initially fixing our attention on one normal mode, Qk, we could get
\( \alpha_{ij} =\left (\alpha_{ij} \right )_{0} +\left (\frac{\partial \alpha_{ij} }{\partial Q_{k}} \right )_{0}Q_{k}\)
As for a harmonic vibration,
\[ Q_{k}=Q_{k0} \cos \left ( \omega_k t + \delta _k \right )\]
Then we could get the expression of α tensor resulting from k-th vibration,
\( \mathbf{\alpha}_{k}=\mathbf{\alpha }_{0}+\left (\frac{\partial \mathbf{\alpha}_{k}}{\partial Q_{k}} \right )_{0}Q_{k0}\cos\left (\omega_{k} t+\delta _{k} \right )\)
Now, under the influence of electromagnetic radiation at frequency ω0, the induced electric dipole moment μ(1) is expressed,
\[ \mathbf{\mu} ^{\left (1 \right )}=\mathbf{\alpha} _{k}\cdot \mathbf{E}_{0}\cos\omega_{0} t=\mathbf{\alpha} _{0}\cdot \mathbf{E}_{0}\cos\omega_{0} t+\left (\frac{\partial \mathbf{\alpha} _{k}}{\partial Q_{k}} \right )_{0}\cdot \mathbf{E}_{0}Q_{k0}\cos\omega_{0} t\cos\left (\omega_{k} t+\delta _{k} \right )t =\]
\[\mathbf{\alpha}_{0}\cdot \mathbf{E}_{0}\cos\omega_{0} t+\dfrac{1}{2}\left (\frac{\partial \mathbf{\alpha}_{k}}{\partial Q_{k}} \right )_{0}\cdot \mathbf{E}_{0}Q_{k0}\cos\left (\omega_{0} t+\omega_{k} t+\delta_k \right )+\dfrac{1}{2}\left (\dfrac{\partial \mathbf{\alpha}_{k}}{\partial Q_{k}} \right )_{0}\cdot \mathbf{E}_0 Q_{k0}\cos\left (\omega_{0}t-\omega_{k} t-\delta_{k} \right )\]
We see that the linear induced dipole moment μ(1) has three components with different frequencies,
\(\mathbf{\alpha} _{0}\cdot \mathbf{E}_{0}\cos\omega_{0} t\) which gives rise to radiation at ω0 and accounts for the Rayleigh scattering;
which gives rise to radiation at ω0+ωk and accounts for the anti-Stokes Raman scattering; and
\[\frac{1}{2}\left(\frac{\partial \mathbf{\alpha}_{k}}{\partial Q_{k}}\right)_{0}\cdot\mathbf{E}_{0}Q_{k0}\cos\left(\omega_{0}t\omega_{k}t\delta_{k}\right)\]
which gives rise to radiation at ω0-ωk and accounts for the Stokes Raman scattering.
From these mathematical manipulations, there emerges a useful qualitative picture of the mechanisms of Rayleigh and Raman scattering in terms of classical radiation theory. Rayleigh scattering comes from the dipole oscillating at ω0 induced in the molecule by the electric field of the incident radiation at frequency ω0. Raman scattering arises from the dipole moment oscillating at ω0±ωk produced by the modulation of dipole oscillating at ω0 with molecular vibration at frequency ωk. In other words, the frequencies we observe in Raman scattering are beat frequencies of the radiation frequency ω0 and the molecular vibrational frequency ωk.
Quantum mechanical treatment
According to the quantum theory, radiation is emitted or absorbed as a result of a system making a downward or upward transition between two discrete energy levels. A quantum theory of spectroscopic processes should, therefore, treat the radiation and molecule together as a complete system, and explore how energy is transferred between the radiation and the molecule as a result of their interaction.
A transition between energy levels of the molecular systems takes place with the emission or absorption of radiation, provided a transition moment associated with the initial and final molecular states is non-zero. The transition moment could be defined as
\( \mathbf{M}_{fi}=\left \langle \Psi _{f}\mid \mathbf{\mu} \mid \Psi _{i}\right \rangle\)
in the Dirac bracket notation, where Ψi and Ψf are the wave function of initial and final states, respectively, and μ is the dipole moment operator.
As we have discussed in the classical part, the linear induced dipole moment could be expressed by
\[ \mathbf{\mu}^{\left (1 \right )}=\mathbf{\alpha} \cdot \mathit{\mathbf{E}}\]
Therefore, in quantum mechanical treatment, if a transition from an initial state to a final state is induced by incident radiation at frequency ω0, the transition moment is given by
\[ \mathbf{\mu} _{fi}^{\left (1 \right )}=\left \langle \Psi _{f}\mid \mathbf{\alpha } \mid \Psi _{i}\right \rangle\cdot \mathbf{E}\]
Now we will examine in more detail the nature of a typical matrix element of the polarizability tensor, like [αxy]fi, for Raman scattering. Just like in the classical theory, we will ignore the rotational wave function and consider the vibrational part only.
\[ \left [\alpha _{xy} \right ]_{fi}=\left \langle \Phi _{f}\mid \alpha_{xy} \mid \Phi _{i}\right \rangle\]
where Φ is the vibrational wave function.
In classical theory,
\[ \alpha_{xy} =\left (\alpha_{xy} \right )_{0} +\sum_{k} \left (\frac{\partial \alpha_{xy} }{\partial Q_{k}} \right )_{0}Q_{k}+\frac{1}{2}\sum_{k,l}\left (\frac{\partial^2 \alpha_{ij}}{\partial Q_{k}\partial Q_{l}} \right )_{0}Q_{k}Q_{l}+\cdots \]
Introducing the quantum part, we obtain (just consider the first order term)
\( \left [\alpha _{xy} \right ]_{fi}=\left (\alpha _{xy} \right )_{0}\left \langle \Phi _{f}\mid \Phi _{i}\right \rangle+\sum_{k}\left (\frac{\partial \alpha _{xy}}{\partial Q_{k}} \right )_{0}\left \langle \Phi _{f}\mid Q_{k}\mid \Phi _{i}\right \rangle\)
In the harmonic oscillator model, the total vibrational wave function is product of the harmonic oscillator wave functions for each of the normal modes of vibration. Thus, for Φ,
\[ \Phi _{i}=\prod_{k}\Phi _{v_{k}^{i}}\left (Q_{k} \right )\]
where \(\Phi _{v_{k}^{i}}\left (Q_{k} \right )\) is the harmonic oscillator wave function associated with the normal coordinate Qk, which has a vibrational quantum number vki in a certain state. For harmonic oscillator functions, we have
and
\[ \left \langle \Phi _{v_{k}^{f}}\left (Q_{k} \right )\mid Q_{k}\mid \Phi _{v_{k}^{i}}\left (Q_{k} \right )\right \rangle=\left\{\begin{matrix} 0 \; \; for \; v_{k}^{f}= v_{k}^{i}\\ \left (v_{k}^{i}+1 \right )^{\frac{1}{2}}b_{v_{k}}\; \; for \; v_{k}^{f}= v_{k}^{i}+1 \\ \left (v_{k}^{i} \right )^{\frac{1}{2}}b_{v_{k}}\; \; for \; v_{k}^{f}= v_{k}^{i}-1 \end{matrix}\right.\]
where
\[ b_{v_{k}}=\sqrt{\frac{h}{8\pi^{2} v_{k}}}\]
Selection rules
We are now able to find out the conditions which have to be satisfied if the transition moment is non-zero. We will consider the zero order term which accounts for the Rayleigh scattering part first. This term is none-zero only if \(v_{k}^{f}=v_{k}^{i}\) which means none of the vibrational quantum numbers change during this transition from initial state i to final state f. Thus, for Rayleigh scattering, the quantum mechanical treatment and the classical theory give the same results.
Then we could go to the first order term \(\sum_{k}\left (\frac{\partial \alpha _{xy}}{\partial Q_{k}} \right )_{0}\left \langle \Phi _{f}\mid Q_{k}\mid \Phi _{i}\right \rangle\) which accounts for the Raman scattering part. For the k-th summand, it is zero unless every term in the product is non-zero, and to achieve this the following conditions must be satisfied, for all modes except the k-th: the vibrational quantum numbers must be the same during the transition, i.e. \(v_{j}^{f}=v_{j}^{i}\) where j≠k; and, for the k-th mode, and the vibrational quantum number must change by one unit, i.e. \(v_{k}^{f}=v_{k}^{i}\pm 1\). The transition moment is associated with Stokes Raman scattering for Δvk=1, and with anti-Stokes Raman scattering for Δvk=-1. These conditions are a result of the properties of harmonic oscillator wave functions.
It follows from these arguments that, in the harmonic approximation, only vibrational fundamentals, i.e., transitions with only one vibrational quantum number changes by one unit, can be observed in the Raman scattering. However, this Δvk=±1 restriction is only a necessary but not a sufficient condition for the occurrence of Raman scattering at the k-th vibrational mode. The vibrational mode should be Raman active, i.e., at least one of the elements of the derived polarizability tensor should be non-zero.
It can be rigorously established by group theory that the elements of the derived polarizability will be non-zero only if they have the same symmetry with the second order terms, i.e., x2, y2, z2, xy, yz, xz. In other words, the irreducible representation of a certain vibrational mode should have a basis in x2, y2, z2, xy, yz or xz.
Finally, we could establish a much better basis for determining selection rules for vibrational transitions in the Raman effect, if we consider the properties of the vibrational transition polarizability components, rather than the derived prolarizability tensor components. For fundamental vibrational transitions, where in the initial state all vibrational quantum numbers are zero and in the final state only the k-th vibrational quantum number has changed to unity,
\( \left [\alpha _{xy} \right ]_{fi}=\left \langle \Phi _{1}\mid \alpha_{xy} \mid \Phi _{0}\right \rangle\)
According to the group theory, this integral will be non-zero, only if αxy and Φ1(Qk) belong to the same symmetry species, which implies that, under each symmetry operation of the molecule in question, αxy and Φ1(Qk) transform in the same way. This constitutes a general selection rule for the Raman activity of a fundamental transition.
In its most general way, covering all types of transitions, the selection rule is as follows: a transition between two states, Ψiand Ψf, is Raman forbidden unless at least one of the triple products of the type ΨiαxyΨf belongs to a representation whose structure contains the totally symmetric species.
References
- Long, D.A., Raman Spectoscopy, McGraw-Hill, Inc., New York, 1977.
- Szymanski, H. A., Raman Spectroscopy: Theory and Practice, Plenum Press, New York, 1967.
- McCreery, R. L., Raman Spectroscopy for Chemical Analysis, John Wiley & Sons, Inc., New York, 2000.
- Stencel, J. M., Raman Spectroscopy for Catalysis, Van Nostrand Reinhold, New York, 1990.
- Grasselli, J. G.; Bulkin, B. J., Analytical Raman Spectroscopy, John Wiley & Sons, Inc., New York, 1991.
- Harris, D. C.; Bertolucci, M. D.; Symmetry and Spectroscopy: an introduction to vibrational and electronic spectroscopy, Dover Publications, Inc., New York, 1989.

