Mössbauer Spectroscopy
- Page ID
- 1787
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Mössbauer spectroscopy is a versatile technique used to study nuclear structure with the absorption and re-emission of gamma rays, part of the electromagnetic spectrum. The technique uses a combination of the Mössbauer effect and Doppler shifts to probe the hyperfine transitions between the excited and ground states of the nucleus. Mössbauer spectroscopy requires the use of solids or crystals which have a probability to absorb the photon in a recoilless manner, many isotopes exhibit Mössbauer characteristics but the most commonly studied isotope is 57Fe.
Introduction
Rudolf L. Mössbauer became a physics student at Technical University in Munich at the age of 20. After passing his intermediate exams Mössbauer began working on his thesis and doctorate work in 1955, while working as an assistant lecturer at Institute for Mathematics. In 1958 at the age of 28 Mössbauer graduated, and also showed experimental evidence for recoilless resonant absorption in the nucleus, later to be called the Mössbauer Effect. In 1961 Mössbauer was awarded the Nobel Prize in physics and, under the urging of Richard Feynman, accepted the position of Professor of Physics at the California Institute of Technology.
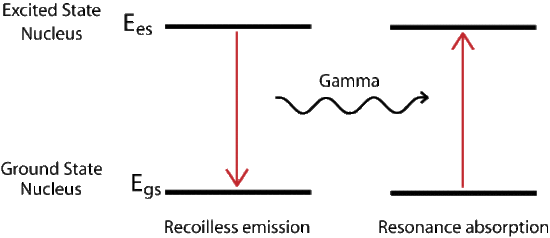
Mössbauer Effect
The recoil energy associated with absorption or emission of a photon can be described by the conservation of momentum. In it we find that the recoil energy depends inversely on the mass of the system. For a gas the mass of the single nucleus is small compared to a solid. The solid or crystal absorbs the energy as phonons, quantized vibration states of the solid, but there is a probability that no phonons are created and the whole lattice acts as the mass, resulting in a recoilless emission of the gamma ray. The new radiation is at the proper energy to excite the next ground state nucleus. The probability of recoilless events increases with decreasing transition energy.
\[P_R = P_{\gamma} \nonumber \]
\[P^2_\gamma = P^2_{\gamma} \nonumber \]
\[2 M E_R = \dfrac{E^2_{\gamma}}{c^2} \nonumber \]
\[E_R = \dfrac{E^2_\gamma}{2M{c^2}} \nonumber \]
Doppler Effect
The Doppler shift describes the change in frequency due to a moving source and a moving observer. \(f\) is the frequency measured at the observer, \(v\) is the velocity of the wave so for our case this is the speed of light \(c\), \(v_r\) is the velocity of the observer, \(v_s\) is the velocity of the source which is positive when heading away from the observer, and \(f_0\) is the initial frequency.
\[f = {\left (\dfrac{v+v_r}{v+v_s}\right)} f_0 \nonumber \]
\[f = {\left (\dfrac{c}{c+v_s}\right)} f_0 \nonumber \]
In the case where the source is moving toward a stationary observer the perceived frequency is higher. For the opposite situation where the source travels away from the observer frequencies recorded at the observer will be of lower compared to the initial wave. The energy of a photon is related to the product of Planck's constant and the frequency of the electromagnetic radiation. Thus for increasing frequencies the corresponding energy also increase, and the same is true in the reverse case where frequencies decrease and therefore energy decreases.
\[E = \dfrac{hc}{\lambda} = hv \nonumber \]
The energy differences between hyperfine states are minimal (fractions of an eV) and the energy variation is achieved by the moving the source toward and away from the sample in an oscillating manner, commonly at a velocity of a few mm/s. The transmittance is then plotted against the velocity of the source and a peak is seen at the energy corresponding to the resonance energy.
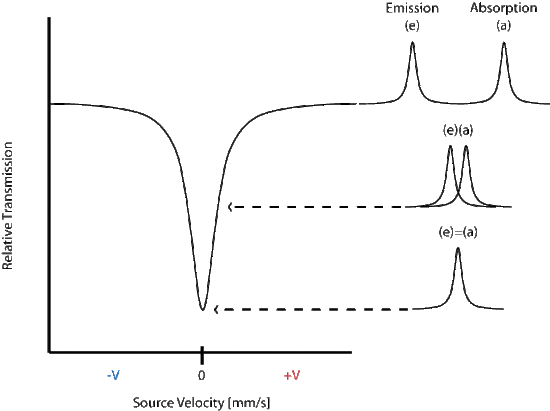
In the above spectrum the emission and absorption are both estimated by the Lorentzian distribution.
Mössbauer Isotopes
By far the most common isotopes studied using Mössbauer spectroscopy is 57Fe, but many other isotopes have also displayed a Mössbauer spectrum. Two criteria for functionality are 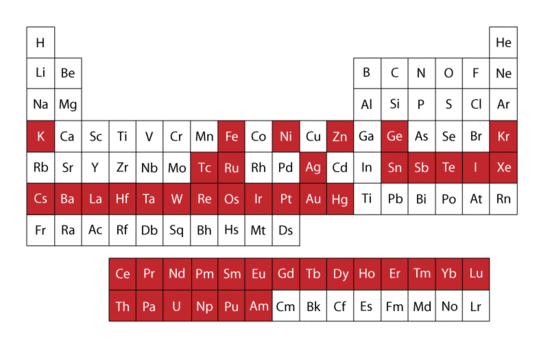
- The excited state is of very low energy, resulting in a small change in energy between ground and excited state. This is because gamma rays at higher energy are not absorbed in a recoil free manner, meaning resonance only occurs for gamma rays of low energy.
- The resolution of Mössbauer spectroscopy depends upon the lifetime of the excited state. The longer the excited state lasts the better the image.
Both conditions are met by 57Fe and it is thus used extensively in Mössbauer spectroscopy. In the figure to the right the red colored boxes of the periodic table of elements indicate all elements that have isotopes visible using the Mössbauer technique.
Hyperfine Interactions
Mössbauer spectroscopy allows the researcher to probe structural elements of the nucleus in several ways, termed isomer shift, quadrupole interactions, and magnetic splitting. These are each explained by the following sections as individual graphs, but in practice Mössbauer spectrum are likely to contain a combination of all effects.
Isomer Shift
An isomeric shift occurs when non identical atoms play the role of source and absorber, thus the radius of the source, \(R_s\), is different that of the absorber, \(R_a\), and the same holds that the electron density of each species is different. The Coulombic interactions affects the ground and excited state differently leading to a energy difference that is not the same for the two species. This is best illustrated with the equation:
\[R_A \neq R_S \nonumber \]
\[\rho_S \neq \rho_S \nonumber \]
\[E_A \neq E_S \nonumber \]
\[\delta = E_A-E_S = \dfrac{2}{3}nZ{e^2}{(\rho_A - \rho_S)}(R^2_{es} - R^2_{gs}) \nonumber \]
Where delta represents the change in energy necessary to excite the absorber, which is seen as a shift from the Doppler speed 0 to V1. The isomer shift depends directly on the s-electrons and can be influenced by the shielding p, d, f electrons. From the measured delta shift there is information about the valance state of the absorbing atom
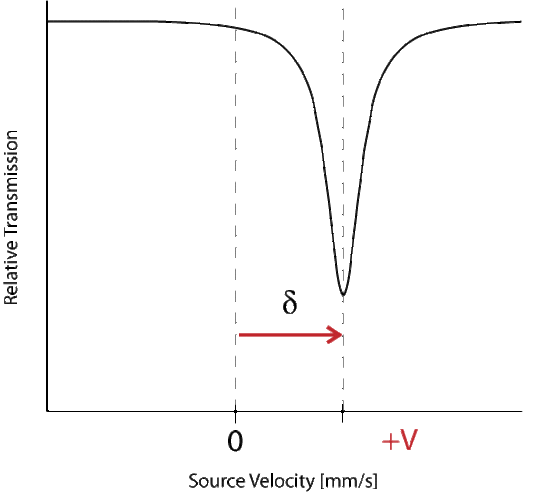
The energy level diagram for \(\delta\) shift shows the change in source velocity due to different sources used. The shift may be either positive or negative.
Quadrupole Interaction
The Hamiltonian for quadrupole interaction using \({}^{57}Fe\) nuclear excited state is given by
\[H_Q = \dfrac{eQV_{ZZ}}{12}[3I^2_Z-I(I+1) + \eta(I^2_X-I^2_y)] \nonumber \]
where the nuclear excited states are split into two degenerate doublets in the absence of magnetic interactions. For the asymmetry parameter \(\eta = 0\) doublets are labeled with magnetic quantum numbers \(m_{es} = \pm 3/2\) and \(m_{es} = \pm 1/2\), where the \(m_{es} = \pm 3/2\) doublet has the higher energy. The energy difference between the doublets is thus
\[\Delta{EQ} = \dfrac{eQV_{zz}}{2}\sqrt{1+\dfrac{\eta^2}{3}} \nonumber \]
The energy diagram and corresponding spectrum can be seen as
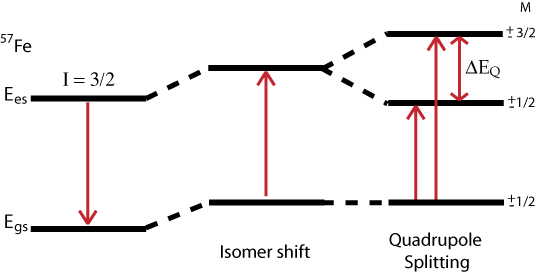
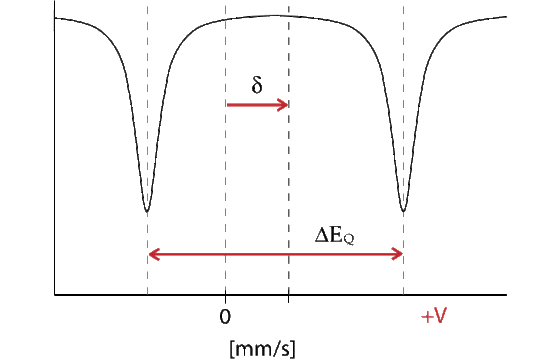
Magnetic Splitting
Magnetic splitting of seen in Mössbauer spectroscopy can be seen because the nuclear spin moment undergoes dipolar interactions with the magnetic field
\[E(m_I) = -g_n{\beta_n}{B_{eff}}m_I \tag{14} \]
where \(g_n\) is the nuclear g-factor and \(\beta_n\) is the nuclear magneton. In the absence of quadrupole interactions the Hamiltonian splits into equally spaced energy levels of
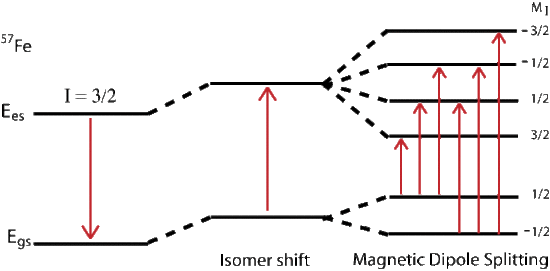

The allowed gamma stimulated transitions of nuclear excitation follows the magnetic dipole transition selection rule:
\[ \Delta I = 1 \nonumber \]
and
\[\Delta m_I = 0, \pm 1 \nonumber \]
where \(m_I\) is the magnetic quantum number and the direction of \(\beta\) defines the nuclear quantization axis. If we assume \(g\) and \(A\) are isotropic (direction independent) where \(g_x = g_y = g_z\) and \(B\) is actually a combination of the applied and internal magnetic fields:
\[H = g\beta{S}\centerdot{B}+AS\centerdot{I} - g_n\beta_nB\centerdot{I} \nonumber \]
The electronic Zeeman term is far larger then the nuclear Zeeman term, meaning the electronic term dominates the equation so \(S\) is approximated by \( \langle S \rangle\) and
\[ \langle S_z\rangle = m_s = \pm \dfrac{1}{2} \nonumber \]
and
\[\langle S_x \rangle = \langle S_y \rangle \approx 0 \nonumber \]
\[H_n = A \langle S \rangle \centerdot{I} - g_n\beta_nB\centerdot{I} \nonumber \]
Pulling out a \(-g_n\beta_n\) followed by \(I\) leaves
\[H_n = -g_n\beta_n \left( -\dfrac{A \langle S \rangle}{g_n\beta_n} + B\right){I} \nonumber \]
Substituting the internal magnetic field with
\[B_{int} = -\dfrac{A \langle S \rangle }{g_n\beta_n} \nonumber \]
results in a combined magnetic field term involving both the applied magnetic field and the internal magnetic field
\[H_n = -g_n\beta_n(B_{int} + B)\centerdot{I} \nonumber \]
which is simplified by using the effective magnetic field \(B_{eff}\)
\[H_n = -g_n\beta_nB_{eff}\centerdot{I} \nonumber \]
References
- Gütlich, P. , Link, R. , & Trautwein, A. (1978). Mössbauer spectroscopy and transition metal chemistry. Inorganic chemistry concepts, v. 3. Berlin: Springer-Verlag.
- G J Long and F Grandjean (1993) Mössbauer Spectroscopy Applied to Magnetism and Materials. New York. , Science Vol. 1,, eds.
- Lawrence Que, J. , Ed. (2000). Physical Methods in Bioinorganic Chemistry. Sausalito, CA, University Science Books.
- Filatov, M. (2007). "On the calculation of Mössbauer isomer shift. " The Journal of Chemical Physics 127(8): 8.
- Introduction to mossbauer spectroscopy. 2013]. Available from http://www. rsc. org/Membership/Networking/InterestGroups/MossbauerSpect/part2. asp.
- Bubek, Moritz, and Dennis Rettinger. 2004. Mossbauer-effekt.
- Haskins, J. R. 1965. Advanced mossbauer-effect experiments. American Journal of Physics: 646.
- Kistner, O. C. , and A. W. Sunyar. 1960. Evidence for quadrupole interaction of Fe57m, and influence of chemical binding on nuclear gamma-ray energy. Physical Review Letters 4 (8): 412.
- Preston, R. S. , S. S. Hanna, and J. Heberle. 1962. Mössbauer effect in metallic iron. Physical Review 128 (5): 2207.
Problems
- The magnetic splitting of \(m_I = 0\) intensity of transition is related to \(sin^2(\theta)\) of the angle between the incoming gamma ray and the effective magnetic field. When is the intensity of transition at max?
- Why is it important for the sample to be in solid or crystalline state?
- What case will result in a delta shift of 0. 00 mm/s?
- Why is the Doppler effect important to Mössbauer spectroscopy?
- Why are both the emission and absorption distributions the same? (both estimated with Lorentzian functions)

