Jablonski diagram
- Page ID
- 1769
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aleksander Jablonski was a Polish academic who devoted his life to the study of molecular absorbance and emission of light. He developed a written representation that generally shows a portion of the possible consequences of applying photons from the visible spectrum of light to a particular molecule. These schematics are referred to as Jablonski diagrams.
Introduction
A Jablonski diagram is basically an energy diagram, arranged with energy on a vertical axis. The energy levels can be quantitatively denoted, but most of these diagrams use energy levels schematically. The rest of the diagram is arranged into columns. Every column usually represents a specific spin multiplicity for a particular species. However, some diagrams divide energy levels within the same spin multiplicity into different columns. Within each column, horizontal lines represent eigenstates for that particular molecule. Bold horizontal lines are representations of the limits of electronic energy states. Within each electronic energy state are multiple vibronic energy states that may be coupled with the electronic state. Usually only a portion of these vibrational eigenstates are represented due to the massive number of possible vibrations in a molecule. Each of these vibrational energy states can be subdivided even further into rotational energy levels; however, typical Jablonski diagrams omit such intense levels of detail. As electronic energy states increase, the difference in energy becomes continually less, eventually becoming a continuum that can be approach with classical mechanics. Additionally, as the electronic energy levels get closer together, the overlap of vibronic energy levels increases.
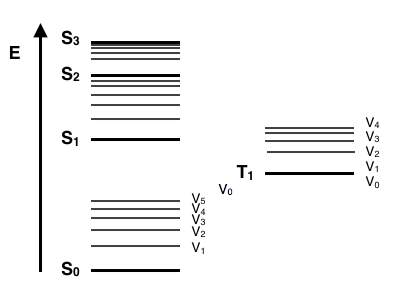
Through the use of straight and curved lines, these figures show transitions between eigenstates that occur from the exposure of a molecule to a particular wavelength of light. Straight lines show the conversion between a photon of light and the energy of an electron. Curved lines show transitions of electrons without any interaction with light. Within a Jablonski diagram several different pathways show how an electron may accept and then dissipate the energy from a photon of a particular wavelength. Thus, most diagrams start with arrows going from the ground electronic state and finish with arrows going to the ground electronic state.
Absorbance
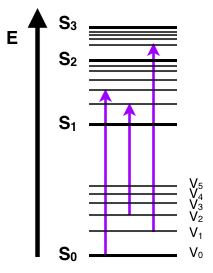
The first transition in most Jablonski diagrams is the absorbance of a photon of a particular energy by the molecule of interest. This is indicated by a straight arrow pointing up. Absorbance is the method by which an electron is excited from a lower energy level to a higher energy level. The energy of the photon is transferred to the particular electron. That electron then transitions to a different eigenstate corresponding to the amount of energy transferred. Only certain wavelengths of light are possible for absorbance, that is, wavelengths that have energies that correspond to the energy difference between two different eigenstates of the particular molecule. Absorbance is a very fast transition, on the order of 10-15 seconds. Most Jablonski diagrams, however, do not indicate a time scale for the phenomenon being indicated. This transition will usually occur from the lowest (ground) electronic state due to the statistical mechanical issue of most electrons occupying a low lying state at reasonable temperatures. There is a Boltzmann distribution of electrons within this low lying levels, based on the the energy available to the molecules. This energy available is a function of the Boltzmann's constant and the temperature of the system. These low lying electrons will transition to an excited electronic state as well as some excited vibrational state.
Vibrational Relaxation and Internal Conversion
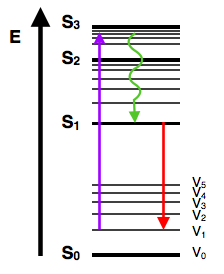
Once an electron is excited, there are a multitude of ways that energy may be dissipated. The first is through vibrational relaxation, a non-radiative process. This is indicated on the Jablonski diagram as a curved arrow between vibrational levels. Vibrational relaxation is where the energy deposited by the photon into the electron is given away to other vibrational modes as kinetic energy. This kinetic energy may stay within the same molecule, or it may be transferred to other molecules around the excited molecule, largely depending on the phase of the probed sample. This process is also very fast, between 10-14 and 10-11 seconds. Since this is a very fast transition, it is extremely likely to occur immediately following absorbance. This relaxation occurs between vibrational levels, so generally electrons will not change from one electronic level to another through this method.
However, if vibrational energy levels strongly overlap electronic energy levels, a possibility exists that the excited electron can transition from a vibration level in one electronic state to another vibration level in a lower electronic state. This process is called internal conversion and mechanistically is identical to vibrational relaxation. It is also indicated as a curved line on a Jablonski diagram, between two vibrational levels in different electronic states. Internal Conversion occurs because of the overlap of vibrational and electronic energy states. As energies increase, the manifold of vibrational and electronic eigenstates becomes ever closer distributed. At energy levels greater than the first excited state, the manifold of vibrational energy levels strongly overlap with the electronic levels. This overlap gives a higher degree of probability that the electron can transition between vibrational levels that will lower the electronic state. Internal conversion occurs in the same time frame as vibrational relaxation, therefore, is a very likely way for molecules to dissipate energy from light perturbation. However, due to a lack of vibrational and electronic energy state overlap and a large energy difference between the ground state and first excited state, internal conversion is very slow for an electron to return to the ground state. This slow return to the ground state lets other transitive processes compete with internal conversion at the first electronically excited state. Both vibrational relaxation and internal conversion occur in most perturbations, yet are seldom the final transition.

Fluorescence
Another pathway for molecules to deal with energy received from photons is to emit a photon. This is termed fluorescence. It is indicated on a Jablonski diagram as a straight line going down on the energy axis between electronic states. Fluorescence is a slow process on the order of 10-9 to 10-7 seconds; therefore, it is not a very likely path for an electron to dissipate energy especially at electronic energy states higher than the first excited state. While this transition is slow, it is an allowed transition with the electron staying in the same multiplicity manifold. Fluorescence is most often observed between the first excited electron state and the ground state for any particular molecule because at higher energies it is more likely that energy will be dissipated through internal conversion and vibrational relaxation. At the first excited state, fluorescence can compete in regard to timescales with other non-radiative processes. The energy of the photon emitted in fluorescence is the same energy as the difference between the eigenstates of the transition; however, the energy of fluorescent photons is always less than that of the exciting photons. This difference is because energy is lost in internal conversion and vibrational relaxation, where it is transferred away from the electron. Due to the large number of vibrational levels that can be coupled into the transition between electronic states, measured emission is usually distributed over a range of wavelengths.
Intersystem Crossing
Yet another path a molecule may take in the dissipation of energy is called intersystem crossing. This where the electron changes spin multiplicity from an excited singlet state to an excited triplet state. It is indicated by a horizontal, curved arrow from one column to another. This is the slowest process in the Jablonski diagram, several orders of magnitude slower than fluorescence. This slow transition is a forbidden transition, that is, a transition that based strictly on electronic selection rules should not happen. However, by coupling vibrational factors into the selection rules, the transition become weakly allowed and able to compete with the time scale of fluorescence. Intersystem crossing leads to several interesting routes back to the ground electronic state. One direct transition is phosphorescence, where a radiative transition from an excited triplet state to a singlet ground state occurs.This is also a very slow, forbidden transition. Another possibility is delayed fluorescence, the transition back to the first excited singlet level, leading to the emitting transition to the ground electronic state.
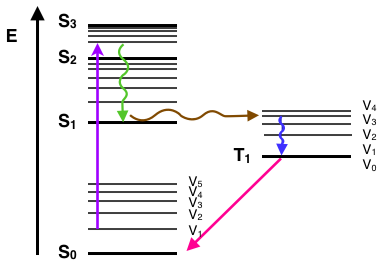
Other non-emitting transitions from excited state to ground state exist and account for the majority of molecules not exhibiting fluorescence or phosphorescent behavior. One process is the energy transfer between molecules through molecular collisions (e.g., external conversion). Another path is through quenching, energy transfer between molecules through overlap in absorption and fluorescence spectra. These are non-emitting processes that will compete with fluorescence as the molecule relaxes back down to the ground electronic state. In a Jablonski diagram, each of these processes are indicated with a curved line going down to on the energy scale.
Time Scales
It is important to note that a Jablonski diagram shows what sorts of transitions that can possibly happen in a particular molecule. Each of these possibilities is dependent on the time scales of each transition. The faster the transition, the more likely it is to happen as determined by selection rules. Therefore, understanding the time scales each process can happen is imperative to understanding if the process may happen. Below is a table of average time scales for basic radiative and non-radiative processes.
| Transition | Time Scale | Radiative Process? |
|---|---|---|
| Internal Conversion | 10-14 - 10-11 s | no |
| Vibrational Relaxation | 10-14 - 10-11 s | no |
| Absorption | 10-15 s | yes |
| Phosphorescence | 10-4 - 10-1 s | yes |
| Intersystem Crossing | 10-8 - 10-3 s | no |
| Fluorescence | 10-9 - 10-7 s | yes |
Each process outlined above can be combined into a single Jablonski diagram for a particular molecule to give a overall picture of possible results of perturbation of a molecule by light energy. Jablonski diagrams are used to easily visualize the complex inner workings of how electrons change eigenstates in different conditions. Through this simple model, specific quantum mechanical phenomena are easily communicated.
References
- H. H. Jaffe and Albert L. Miller "The fates of electronic excitation energy" J. Chem. Educ., 1966, 43 (9), p 469 DOI:10.1021/ed043p469
- E. B. Priestley and A. Haug "Phosphorescence Spectrum of Pure Crystalline Naphthalene" J. Chem. Phys. 49, 622 (1968), DOI:10.1063/1.1670118

