Metal to Ligand and Ligand to Metal Charge Transfer Bands
- Page ID
- 1773
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the field of inorganic chemistry, color is commonly associated with d–d transitions. If this is the case, why is it that some transition metal complexes show intense color in solution, but possess no d electrons? In transition metal complexes a change in electron distribution between the metal and a ligand gives rise to charge transfer (CT) bands when performing Ultraviolet-visible spectroscopy experiments. For complete understanding, a brief introduction to electron transfer reactions and Marcus-Hush theory is necessary.
Outer Sphere Charge Transfer Reactions
Electron transfer reactions(charge transfer) fall into two categories: Inner-sphere mechanisms and Outer-sphere mechanisms. Inner-sphere mechanisms involve electron transfer occurring via a covalently bound bridging ligand (Figure \(\PageIndex{1}\)).

Outer-sphere mechanisms involve electron transfer occurring without a covalent linkage between reactants, e.g.,
\[\ce{[ML6]^{2+} + [ML6]^{3+} -> [ML6]^{3+} + [ML6]^{2+}} \label{eq1}\]
Here, we focus on outer sphere mechanisms.
In a self-exchange reaction the reactant and product side of a reaction are the same. No chemical reaction takes place and only an electron transfer is witnessed. This reductant-oxidant pair involved in the charge transfer is called the precursor complex. The Franck-Condon approximation states that a molecular electronic transition occurs much faster than a molecular vibration.
Consider the reaction described in Equation \ref{1}. This process has a Franck-Condon restriction: Electron transfer can only take place when the \(\ce{M–L}\) bond distances in the \(\ce{ML(II)}\) and \(\ce{ML(III)}\) states are the same. This means that vibrationally excited states with equal bonds lengths must be formed in order to allow electron transfer to occur. This would mean that the \(\ce{[ML6]^{2+}}\) bonds must be compressed and \(\ce{[ML6]^{3+}}\) bonds must be elongated for the reaction to occur.
Self exchange rate constants vary, because the activation energy required to reach the vibrational states varies according to the system. The greater the changes in bond length required to reach the precursor complex, the slower the rate of charge transfer.1
A Brief Introduction to Marcus-Hush Theory
Marcus-Hush theory relates kinetic and thermodynamic data for two self-exchange reactions with data for the cross-reaction between the two self-exchange partners. This theory determines whether an outer sphere mechanism has taken place. This theory is illustrated in the following reactions
Self exchange 1: [ ML6 ] 2+ + [ML6] 3+ → [ ML6 ] 3+ + [ ML6 ] 2+ ∆GO = 0
Self exchange 2: [ ML6 ] 2+ + [ML6] 3+ → [ ML6 ] 3+ + [ ML6 ] 2+ ∆GO = 0
Cross Reaction: [ ML6 ] 2+ + [ ML6] 3+ → [ ML6 ] 3+ + [ ML6 ] 2+
The Gibbs free energy of activation \(\Delta G^{\mp }\) is represented by the following equation:
\[\Delta G^{\mp } = \Delta_{w} G^{\mp } + \Delta _{o}G^{\mp } + \Delta _{s}G^{\mp }+ RT \ln ( k’T / hZ) \nonumber \]
- T = temperature in K
- R = molar gas constant
- k’ = Boltzmann constant
- h = Planck's constant
- Z = effective frequency collision in solution ~ 1011 dm3 mol-1 s-1
- ∆wGŦ = the energy associated with bringing the reactants together, includes the work done to counter any repulsion
- ∆0GŦ = energy associated with bond distance changes
- ∆s ∆GŦ= energy associated with the rearrangements taking place in the solvent spheres
- ln ( k’T / hZ) = accounts for the energy lost in the formation of the encounter complex
The rate constant for the self-exchange is calculated using the following reaction
\[k = \kappa Z e^{-\Delta G^{\mp }/RT} \nonumber \]
where \(\kappa\) is the transmission coefficient ~1.
The Marcus-Hush equation is given by the following expression
\[k_{12}=(k_{11}k_{22}K_{12}f_{12})^{1/2} \label{marcus}\]
where:
\[\log f_{12}=\frac{(\log K_{12})^{2}}{4\log(\frac{k_{11}k_{22}}{Z^{2}})} \nonumber \]
- \(Z\) is the collision frequency
- k11 and ∆GŦ11 correspond to self exchange 1
- k22 and ∆GŦ22 correspond to self exchange 2
- k12 and ∆GŦ12 correspond to the cross-reaction
- K12 = cross reaction equilibrium constant
- ∆GO12= standard Gibbs free energy of the reaction
The following equation is an approximate from of the Marcus-Hush equation (Equation \ref{marcus}):
\[\log k_{12}\approx 0.5\log k_{11}+0.5\log \log \nonumber \]
since \(f\approx 1\) and \(\log f \approx 0\).
How is the Marcus-Hush equation used to determine if an outer sphere mechanism is taking place?
- values of k11, k22, K12, and k12 are obtained experimentally
- k11 and k22 are theoretically values
- \(K_{12}\) is obtained from \(E_{cell}\)
If an outer sphere mechanism is taking place the calculated values of \(k_{12}\) will match or agree with the experimental values. If these values do not agree, this would indicate that another mechanism is taking place.1
The Laporte Selection Rule and Weak d–d Transitions
d- d transitions are forbidden by the Laporte selection rule.
- Laporte Selection Rule: \(∆l = + 1\)
- Laporte allowed transitions: a change in parity occurs i.e. s → p and p → d.
- Laporte forbidden transitions: the parity remains unchanged i.e. p → p and d → d.
d-d transitions result in weak absorption bands and most d-block metal complexes display low intensity colors in solution (exceptions d0 and d10 complexes). The low intensity colors indicate that there is a low probability of a d-d transition occurring.
Ultraviolet-visible (UV/Vis) spectroscopy is the study of the transitions involved in the rearrangements of valence electrons. In the field of inorganic chemistry, UV/Vis is usually associated with d – d transitions and colored transition metal complexes. The color of the transition metal complex solution is dependent on: the metal, the metal oxidation state, and the number of metal d-electrons. For example iron(II) complexes are green and iron(III) complexes are orange/brown.2
Charge Transfer Bands
If color is dependent on d-d transitions, why is it that some transition metal complexes are intensely colored in solution but possess no d electrons?

In transition metal complexes a change in electron distribution between the metal and a ligand give rise to charge transfer (CT) bands.1 CT absorptions in the UV/Vis region are intense (ε values of 50,000 L mole-1 cm-1 or greater) and selection rule allowed. The intensity of the color is due to the fact that there is a high probability of these transitions taking place. Selection rule forbidden d-d transitions result in weak absorptions. For example octahedral complexes give ε values of 20 L mol-1 cm-1 or less.2 A charge transfer transition can be regarded as an internal oxidation-reduction process. 2
Ligand to Metal and Metal to Ligand Charge Transfer Bands
Ligands possess \(σ\), \(σ^*\), \(π\), \(π^*\), and nonbonding (\(n\)) molecular orbitals. If the ligand molecular orbitals are full, charge transfer may occur from the ligand molecular orbitals to the empty or partially filled metal d-orbitals. The absorptions that arise from this process are called ligand-to-metal charge-transfer (LMCT) bands (Figure 3).2 LMCT transitions result in intense bands. Forbidden d-d transitions may also take place giving rise to weak absorptions. Ligand to metal charge transfer results in the reduction of the metal.
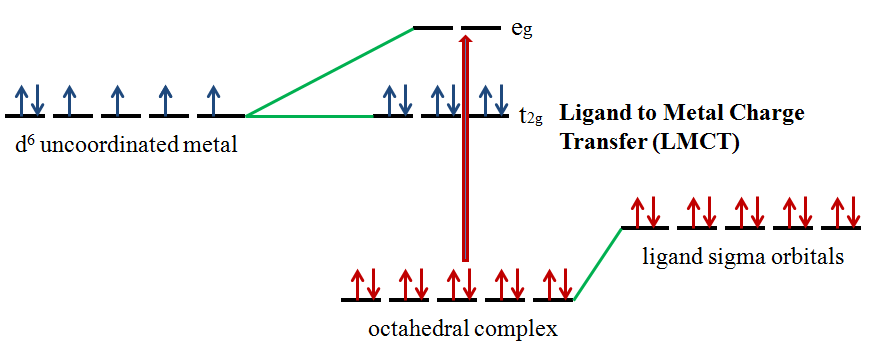
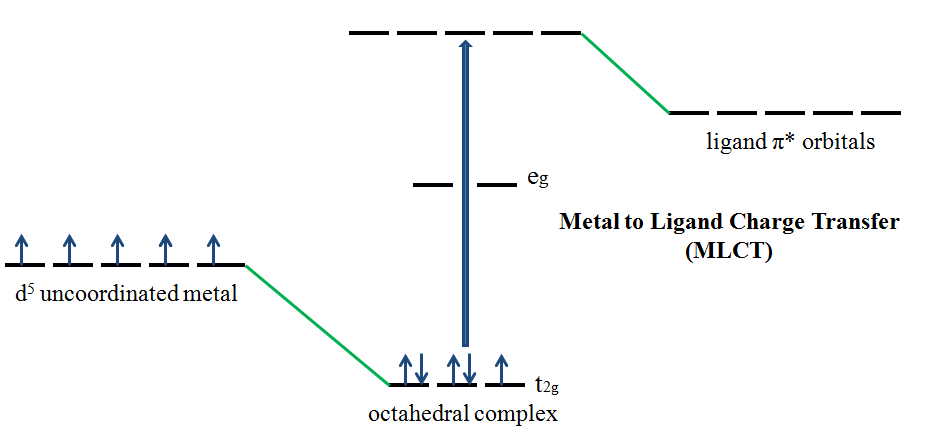
If the metal is in a low oxidation state (electron rich) and the ligand possesses low-lying empty orbitals (e.g., \(\ce{CO}\) or \(\ce{CN^{-}}\)) then a metal-to-ligand charge transfer (MLCT) transition may occur. MLCT transitions are common for coordination compounds having π-acceptor ligands. Upon the absorption of light, electrons in the metal orbitals are excited to the ligand \(π^*\) orbitals.2 Figure 4 illustrates the metal to ligand charge transfer in a d5 octahedral complex. MLCT transitions result in intense bands. Forbidden d–d transitions may also occur. This transition results in the oxidation of the metal.
Effect of Solvent Polarity on CT Spectra
*This effect only occurs if the species being studied is an ion pair*
The position of the CT band is reported as a transition energy and depends on the solvating ability of the solvent. A shift to lower wavelength (higher frequency) is observed when the solvent has high solvating ability.
Polar solvent molecules align their dipole moments maximally or perpendicularly with the ground state or excited state dipoles. If the ground state or excited state is polar an interaction will occur that will lower the energy of the ground state or excited state by solvation. The effect of solvent polarity on CT spectra is illustrated in the following example.
You are preparing a sample for a UV/Vis experiment and you decide to use a polar solvent. Is a shift in wavelength observed when:
a) Both the ground state and the excited state are neutral
When both the ground state and the excited state are neutral a shift in wavelength is not observed. No change occurs. Like dissolves like and a polar solvent won’t be able to align its dipole with a neutral ground and excited state.
b) The excited state is polar, but the ground state is neutral
If the excited state is polar, but the ground state is neutral the solvent will only interact with the excited state. It will align its dipole with the excited state and lower its energy by solvation. This interaction will lower the energy of the polar excited state. (increase wavelength, decrease frequency, decrease energy)

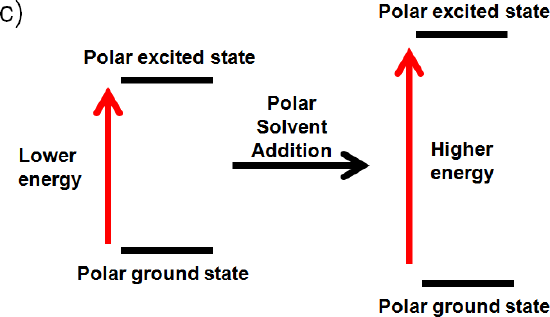
c) The ground state and excited state is polar
If the ground state is polar the polar solvent will align its dipole moment with the ground state. Maximum interaction will occur and the energy of the ground state will be lowered. (increased wavelength, lower frequency, and lower energy) The dipole moment of the excited state would be perpendicular to the dipole moment of the ground state, since the polar solvent dipole moment is aligned with the ground state. This interaction will raise the energy of the polar excited state. (decrease wavelength, increase frequency, increase energy)
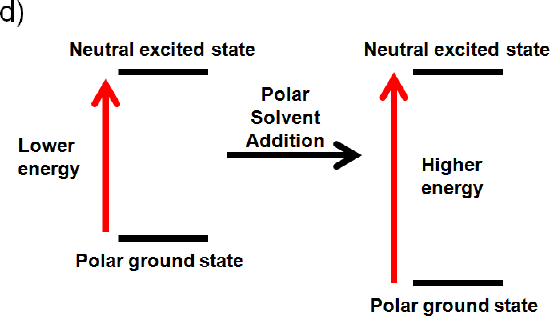
d) The ground state is polar and the excited state is neutral
If the ground state is polar the polar solvent will align its dipole moment with the ground state. Maximum interaction will occur and the energy of the ground state will be lowered. (increased wavelength, lower frequency, and lower energy). If the excited state is neutral no change in energy will occur. Like dissolves like and a polar solvent won’t be able to align its dipole with a neutral excited state. Overall you would expect an increase in energy (Illustrated below), because the ground state is lower in energy (decrease wavelength, increase frequency, increase energy).4
How to Identify Charge Transfer Bands
CT absorptions are selection rule allowed and result in intense (ε values of 50,000 L mole-1 cm-1 or greater) bands in the UV/Vis region.2 Selection rule forbidden d-d transitions result in weak absorptions. For example octahedral complexes give ε values of 20 L mol-1 cm-1 or less.2 CT bands are easily identified because they:
- Are very intense, i.e. have a large extinction coefficient
- Are normally broad
- Display very strong absorptions that go above the absorption scale (dilute solutions must be used)
\(\ce{KMnO4}\) dissolved in water exhibits intense CT Bands. The one LMCT band in the visible is observed around 530 nm.
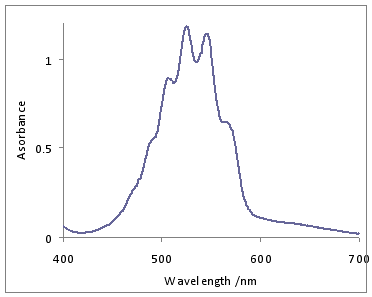
The band at 528 nm gives rise to the deep purple color of the solution. An electron from a “oxygen lone pair” character orbital is transferred to a low lying \(\ce{Mn}\) orbital.1
Tris(bipyridine)ruthenium(II) dichloride (\(\ce{[Ru(bpy)3]Cl2}\)) is a coordination compound that exhbits a CT band is observed (Figure \(\PageIndex{6}\))
ruthenium(II)_chloride.png?revision=1&size=bestfit&width=395&height=280)
32%252B_absorption%2526emission.png?revision=1&size=bestfit&width=445&height=280)
A d electron from the ruthenium atom is excited to a bipyridine anti-bonding orbital. The very broad absorption band is due to the excitation of the electron to various vibrationally excited states of the π* electronic state.6
Practice Problems
- You perform a UV/Vis on a sample. The sample being studied has the ability to undergo a charge transfer transition. A charge transfer transitions is observed in the spectra. Why would this be an issue if you want to detect d-d transitions? How can you solve this problem?
- What if both types of charge transfer are possible? For example a complex has both σ-donor and π-accepting orbitals? Why would this be an issue?
- If the ligand has chromophore functional groups an intraligand band may be observed. Why would this cause a problem if you want to observe charge transfer bands? How would you identify the intraligand bands? State a scenario in which you wouldn’t be able to identify the intraligand bands.
Answers to Practice Problems
- This is an issue when investigating weak d-d transitions, because if the molecule undergoes a charge transfer transitions it results in an intense CT band. This makes the d – d transitions close to impossible to detect if they occur in the same region as the charge transfer band. This problem is solved by performing the UV/Vis experiment on a more concentrated solution, resulting in minor peaks becoming more prominent.
- Octahedral complexes such as Cr(CO)6, have both σ-donor and π-accepting orbitals. This means that they are able to undergo both types of charge transfer transitions. This makes it difficult to distinguish between LMCT and MLCT.
- This would cause a problem because CT bands may overlap intraligand bands. Intraligand bands can be identified by comparing the complex spectrum to the spectrum of the free ligand. This may be difficult, since upon coordination to the metal, the ligand orbital energies may change, compared to the orbital energies of the free ligand. It would be very difficult to identify an intraligand band if the ligand doesn’t exist as a free ligand. If it doesn’t exist as a free ligand you wouldn’t be able to take a UV/Vis, and thus wouldn’t be able to use this spectrum in comparison to the complex spectrum.
Article References
- Housecroft, Catherine E., and A. G. Sharpe. "Outer Sphere Mechanism." Inorganic Chemistry. Harlow, England: Pearson Prentice Hall, 2008. 897-900.
- Brisdon, Alan K. "UV-Visible Spectroscopy." Inorganic Spectroscopic Methods. Oxford: Oxford UP, 1998. 70-73..
- Huheey, James E., Ellen A. Keiter, and Richard L. Keiter. "Coordination Chemistry: Bonding, Spectra, and Magnetism." Inorganic Chemistry: Principles of Structure and Reactivity. New York, NY: HarperCollins College, 1993. 455-59.
- Drago, Russell S. "Effect of Solvent Polarity on Charge-Transfer Spectra." Physical Methods for Chemists. Ft. Worth: Saunders College Pub., 1992. 135-37.
- Miessler, Gary L., and Donald A. Tarr. "Coordination Chemistry III: Electronic Spectra." Inorganic Chemistry. Upper Saddle River, NJ: Pearson Education, 2004. 407-08.
- Paris, J. P., and Warren W. Brandt. "Charge Transfer Luminescence of a Ruthenium(II) Chelate." Communications to the Editor 81 (1959): 5001-002.
Literature: Marcus Theory and Charge Transfer Bands
- Marcus, R. A. "Chemical and Electrochemical Electron-Transfer Theory." Annual Review of Physical Chemistry 15.1 (1964): 155-96.
- Eberson, Lennart. "Electron Transfer Reactions in Organic Chemistry. II* An Analysis of Alkyl Halide Reductions by Electron Transfer Reagents on the Basis of Marcus Theory." Acta Chemica Scandinavica 36 (1982): 533-43.
- Chou, Mei, Carol Creutz, and Norman Sutin. "Rate Constants and Activation Parameters for Outer-sphere Electron-transfer Reactions and Comparisons with the Predictions of Marcus Theory." Journal of the American Chemical Society 99.17 (1977): 5615-623.
- Marcus, R. A. "Relation between Charge Transfer Absorption and Fluorescence Spectra and the Inverted Region." Journal of Physical Chemistry 93 (1989): 3078-086.
Literature: Examples of Charge Transfer Bands
- Electron Transfer Reactions of Fullerenes:
- Mittal, J. P. "Excited States and Electron Transfer Reactions of Fullerenes." Pure and Applied Chemistry 67.1 (1995): 103-10.
- Wang, Y. "Photophysical Properties of Fullerenes/ N,N-diethylanaline Charge Transfer Complexes." Journal of Physical Chemistry 96 (1992): 764-67.
- Vehmanen, Visa, Nicolai V. Tkachenko, Hiroshi Imahori, Shunichi Fukuzumi, and Helge Lemmetyinen. "Charge-transfer Emission of Compact Porphyrin–fullerene Dyad Analyzed by Marcus Theory of Electron-transfer." Spectrochimica Acta Part A 57 (2001): 2229-244.
- Electron Transfer Reactions in RuBpy:
- Paris, J. P., and Warren W. Brandt. "Charge Transfer Luminescence of a Ruthenium(II) Chelate." Communications to the Editor 81 (1959): 5001-002.

