16: Molecular Spectroscopy
- Page ID
- 8862
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Our most detailed knowledge of atomic and molecular structure has been obtained from spectroscopy-study of the emission, absorption and scattering of electromagnetic radiation accompanying transitions among atomic or molecular energy levels. Whereas atomic spectra involve only electronic transitions, the spectroscopy of molecules is more intricate because vibrational and rotational degrees of freedom come into play as well. Early observations of absorption or emission by molecules were characterized as band spectra-in contrast to the line spectra exhibited by atoms. It is now understood that these bands reflect closely-spaced vibrational and rotational energies augmenting the electronic states of a molecule. With improvements in spectroscopic techniques over the years, it has become possible to resolve individual vibrational and rotational transitions. This has provided a rich source of information on molecular geometry, energetics and dynamics. Molecular spectroscopy has also contributed significantly to analytical chemistry, environmental science, astrophysics, biophysics and biochemistry.
Reduced Mass
Consider a system of two particles of masses \(m_1\) and \(m_2\) interacting with a potential energy which depends only on the separation of the particles. The classical energy is given by \[E=\frac{1}{2} m_1 \dot{\vec{r}}_1^2+\frac{1}{2} m_2 \dot{\vec{r}}_2^2+V (|\vec{r}_2-\vec{r}_1|) \label{1}\] the dots signifying derivative wrt time. Introduce two new variables, the particle separation \(\vec{r}\) and the position of the center of mass \(\vec{R}\):
\[ \vec{r}=\vec{r}_2-\vec{r}_1 \mbox{,}\hspace{20pt}\vec{R}=\dfrac{m_1 \vec{r}_1+m_2\vec{r}_2}{m}\label{2}\]
where \(m=m_1+m_2\). In terms of the new coordinates
\[\vec{r}_1=\vec{R}+\frac{m_2}{m} \vec{r} \mbox{,}\hspace{20pt}\vec{r}_2=\vec{R}-\frac{m_1}{m} \vec{r}\label{3}\]
and
\[E=\dfrac{1}{2}m\dot{\vec{R}}^2+\dfrac{1}{2}\mu\dot{\vec{r}}^2+V(r)\label{4}\]
where \(r=|\vec{r}|\) and \(\mu\) is called the \(reduced\hspace{2pt}mass\)
\[\mu\equiv\dfrac{m_1 m_2}{m_1+m_2}\label{5}\]
An alternative relation for reduced mass is
\[\dfrac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}\label{6}\]
reminiscent of the formula for resistance of a parallel circuit. Note that, if \(m_2\rightarrow\infty\), then \(\mu\rightarrow m_1\). The term containing \(\dot{\vec{R}}\) represents the kinetic energy of a single hypothetical particle of mass \(\mu\) located at the center of mass \(\vec{R}\). The remaining terms represent the \(relative\) motion of the two particles. It was the appearance of a \(single\) particle of effective mass \(\mu\) moving in the potential field \(V(r)\).
\[E_{rel}=\dfrac{1}{2} \mu \dot{\vec{r}^2}+V(r)= \dfrac{\vec{p}^2}{2\mu}+V(r)\label{7}\]
We can thus write the Schrödinger equation for the relative motion
\[ \left\{-\dfrac{\hbar^2}{2 \mu} \bigtriangledown^2+V(r) \right\}\psi (\vec{r})= E \psi (\vec{r}) \label{8}\]
When we treated the hydrogen atom, it was assumed that the nuclear mass was infinite. In that case we can set \(\mu =m\), the mass of an electron. The Rydberg constant for infinite nuclear mass was calculated to be
\[R_\infty = \dfrac{2\pi^2me^4}{h^3c}=109,737 \text{cm} ^{-1}\label{9}\]
If instead, we use the reduced mass of the electron-proton system
\[\mu = \dfrac{mM}{m+M} \approx \dfrac{1836}{1837}\, m \approx 0.999456 \, m \label{10}\].
This changes the Rydberg constant for hydrogen to
\[R_{H}\approx 109,677 \, cm^{-1}\label{11}\]
in perfect agreement with experiment.
In 1931, H. C. Urey evaporated four liters of hydrogen down to one milliliter and measured the spectrum of the residue. The result was a set of lines displaced slightly from the hydrogen spectrum. This amounted to the discovery of deuterium, or heavy hydrogen, for which Urey was awarded in 1934 Nobel Prize in Chemistry. Estimating the mass of the deuteron, 2H1, as twice that of the proton, gives
\[R_{D}\approx 109,707 \, cm^{-1}\label{12}\]
Another interesting example involving reduced mass concerns positronium, a short-lived combination of an electron and a positron-the electron's antiparticle. The electron and position mutually annihilate with a half-life of approximately 10-7 sec. and positroium decays into gamma rays. The reduced mass of positronium is
\[ \mu = \frac{m \times m}{m+m} = \frac{m}{2} \label{13} \]
half the mass of the electron. Thus the ionization energy equals 6.80 eV, half that of hydrogen atom. Positron emission tomography (PET) provides a sensitive scanning technique for functioning living tissue, notably the brain. A compound containing a positron-emitting radionuclide, for example, 11C, 13N, 15O or 18F, is injected into the body. The emitted positrons attach to electrons to form short-lived positronium, and the annihilation radiation is monitored.
Vibration of Diatomic Molecules
A diatomic molecule with nuclear masses MA, MB has a reduced mass
\[\mu =\frac{M_{A}M_{B}}{M_{A}+M_{B}}\label{14}\]

Solution of the electronic Schrödinger equation gives the energy as a function of internuclear distance Eelec(R). This plays the role of a potential energy function for motion of the nuclei V(R), as sketched in Fig. 2. We can thus write the Schrödinger equation for vibration
\[\begin{Bmatrix}
-\frac{\hbar^2}{2\mu }\frac{d^2}{dR^2} +V(R)\end{Bmatrix}\chi (R)=E_{\chi }(R)\label{15}\]
If the potential energy is expanded in a Taylor series about R = Re
\[V(R)=V(R_{e})+(R-R_{e})V'(R_{e})+\frac{1}{2}(R-R_{e})^2V"(R_{e})+...\label{16}\]
An approximation for this expansion has the form of a harmonic oscillator with
\[V(R)\approx \frac{1}{2}k(R-R_{e})^2\label{17}\]
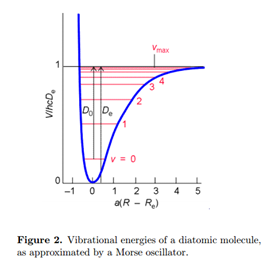
The energy origin can be chosen so V (Re) = 0. At the minimum of the potential, V'(Re) = 0. The best fit to the parabola (17) is obtained with a force constant set equal to
\[k\approx \frac{d^2V(R)}{dR^2}\mid _{R\, =\, R_{e}}\label{18}\]
From the solution for the harmonic oscillator, we identify the ground state vibrational energy, with quantum number \(\nu\) = 0
\[E_{0}=\hbar\omega =\hbar\sqrt{\frac{k}{\mu }}\label{19}\]
The actual dissociation energy from the ground vibrational state is then approximated by
\[D_{0}\approx D_{e}-\frac{1}{2}\hbar\omega\label{20}\]
In wavenumber units
\[hcD_{0}\approx hcD_{e}-\frac{1}{2}\tilde{\nu }\: cm^{-1}\label{21}\]
An improved treatment of molecular vibration must account for anharmonicity, deviation from a harmonic oscillator. Anharmonicity results in a finite number of vibrational energy levels and the possibility of dissociation of the molecule at sufficiently high energy. A very successful approximation for the energy of a diatomic molecule is the Morse potential:
\[V(R)=hcD_{e}\begin{Bmatrix}1-e^{a(R-R_{e})}\end{Bmatrix}^2\; \; \; a=\begin{pmatrix}\frac{\mu \omega ^2}{2hcD_{e}}\end{pmatrix}^{\frac{1}{2}}\label{22}\]
Note that V (Re) = 0 at the minimum of the potential well. The Schrödinger equation for a Morse oscillator can be solved to give the energy levels
\[E_{\upsilon }=(\upsilon +\frac{1}{2})\hbar\omega-(\upsilon+\frac{1}{2} )^2\hbar\omega x_{e}\label{23}\]
or, expressed in wavenumber units,
\[hcE_{\upsilon }=(\upsilon +\frac{1}{2})\tilde{\nu }-(\upsilon +\frac{1}{2})^2x_{e}\tilde{\nu }\label{24}\]
Higher vibrational energy levels are spaced closer together, just as in real molecules. Vibrational transitions of diatomic molecules occur in the infrared, roughly in the range of 50-12,000 cm-1. A molecule will absorb or emit radiation only if it has a non-zero dipole moment. Thus HCl is infrared active while H2 and Cl2 are not.
Vibration of Polyatomic Molecules
A molecule with N atoms has a total of 3N degrees of freedom for its nuclear motions, since each nucleus can be independently displaced in three perpendicular directions. Three of these degrees of freedom correspond to translational motion of the center of mass. For a nonlinear molecule, three more degrees of freedom determine the orientation of the molecule in space, and thus its rotational motion. This leaves 3N - 6 vibrational modes. For a linear molecule, there are just two rotational degrees of freedom, which leaves 3N - 5 vibrational modes. For example, the nonlinear molecule H2O has three vibrational modes while the linear molecule CO2 has four vibrational modes. The vibrations consist of coordinated motions of several atoms in such a way as to keep the center of mass stationary and nonrotating. These are called the normal modes. Each normal mode has a characteristic resonance frequency \(\tilde{\nu _{i}}\), which is usually determined experimentally. To a reasonable approximation, each normal mode behaves as an independent harmonic oscillator of frequency \(\tilde{\nu _{i}}\). The normal modes of H2O and CO2 are pictured below.

A normal mode will be infrared active only if it involves a change in the dipole moment. All three modes of H2O are active. The symmetric stretch of CO2 is inactive because the two C-O bonds, each of which is polar, exactly compensate. Note that the bending mode of CO2 is doubly degenerate. Bending of adjacent bonds in a molecule generally involves less energy than bond stretching, thus bending modes generally have lower wavenumbers than stretching modes.
Rotation of Diatomic Molecules
The rigid rotor model assumes that the internuclear distance R is a constant. This is not a bad approximation since the amplitude of vibration is generally of the order of 1% of R. The Schrödinger equation for nuclear motion then involves the three-dimensional angular momentum operator, written \(\hat{J}\) rather than \(\hat{L}\) when it refers to molecular rotation. The solutions to this equation are already known and we can write
\[\frac{\hat{J}^2}{2\mu R^2}Y_{JM}(\theta ,\phi )=E_{J}Y_{JM}(\theta,\phi)\; \; \; J=0,1,2...\; \; \; M=0,\pm \, 1...\pm\,J\label{25}\]
where YJM(\(\theta,\phi\)) are spherical harmonics in terms of the quantum numbers J and M, rather than l and m. Since the eigenvalues of \(\hat{J}^2\) are \(J(J +1)\hbar^2\), the rotational energy levels are
\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\label{26}\]
The moment of inertia is given by
\[I=\mu R^2=M_{A}R^{2}_{A}+M_{B}R^{2}_{B}\label{27}\]
where RA and RB are the distances from nuclei A and B, respectively, to the center of mass. In wavenumber units, the rotational energy is expressed
\[hcE_{J}=BJ(J+1)cm^{-1}\label{28}\]
where B is the rotational constant. The rotational energy-level diagram is shown in Fig.5. Each level is (2J + 1)-fold degenerate. Again, only polar molecules can absorb or emit radiation in the course of rotational transitions. The radiation is in the microwave or far infrared region. The selection rule for rotational transitions is \(\Delta\)J = \(\pm\)1.

Molecular Parameters from Spectroscopy
Following is a table of spectroscopic constants for the four hydrogen halides:

The force constant can be found from the vibrational constant. Equating the energy quantities \(\hbar\omega=hc\tilde{\nu }\), we find
\[\omega=2\pi c\tilde{\nu }=\sqrt{\frac{k}{\mu }}\label{29}\]
Thus
\[k=(2\pi c\tilde{\nu })^2\mu\label{30}\]
with
\[\mu=\frac{m_{A}m_{B}}{m_{A}+m_{B}}=\frac{M_{A}M_{B}}{M_{A}+M_{B}}u\label{31}\]
where u = 1.66054 x 10-27 kg, the atomic mass unit. MA and MB are the conventional atomic weights of atoms A and B (on the scale 12C = 12). Putting in numerical factors
\[k=58.9\, \times \, 10^{-6}(\tilde{\nu }/cm^{-1})^2\frac{M_{A}M_{B}}{M_{A}+M_{B}}N/m \label{32}\]
This gives 958.6, 512.4, 408.4 and 311.4 N/m for HF, HCl, HBr and HI, respectively. These values do not take account of anharmonicity.
The internuclear distance R is determined by the rotational constant. By definition,
\[hcB=\frac{\hbar^2}{2I}\label{33}\]
Thus
\[B=\frac{\hbar}{4\pi cI}\label{34}\]
with
\[I=\mu R^2=\frac{m_{A}m_{B}}{m_{A}+m_{B}}R^2=\frac{M_{A}M_{B}}{M_{A}+M_{B}}uR^2\; \; kg\: m^2\label{35}\]
Solving for R,
\[R=410.6 / \sqrt{\frac{M_{A}M_{B}}{M_{A}+M_{B}}(B/cm^{-1})}\: \: pm\label{36}\]
For the hydrogen halides, HF, HCl, HBr, HI, we calculate R = 92.0, 127.9, 142.0, 161.5 pm, respectively.
Rotation of Nonlinear Molecules
A nonlinear molecule has three moments of inertia about three principal axes, designated Ia, Ib and Ic. The classical rotational energy can be written
\[E=\dfrac{J^2_{a}}{2I_{a}}+\frac{J^2_{b}}{2I_{b}}+\dfrac{J^2_{c}}{2I_{c}}\label{37}\]
where Ja, Jb, Jc are the components of angular momentum about the principal axes. For a spherical rotor, such as CH4 or SF6, the three moments of inertia are equal to the same value I. The energy simplifies to J2/2I and the quantum-mechanical Hamiltonian is given by
\[\hat{H}=\frac{\hat{J}^2}{2I}\label{38}\]
The eigenvalues are
\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\; \;\; J=0,1,2..\label{39}\]
just as for a linear molecule. But the levels of a spherical rotor have degeneraciesof (2J + 1)2 rather than (2J + 1).
A symmetric rotor has two equal moments of inertia, say Ic = Ib \(\neq \) Ia. The molecules NH3, CH3Cl and C6H6 are examples. The Hamiltonian takes the form
\[ \hat H = \frac{\hat J_a^2}{2I_a}+\frac{\hat J_b^2 + \hat J_c^2}{2I_b} = \frac{\hat J^2}{2I_b} + (\frac{1}{2I_a} - \frac{1}{2I_b}) \hat J_a^2 \label{40} \]
Since it is possible to have simultaneous eigenstates of \(\hat J^2\) and one of its components \(\hat J_a\), the energies of a symmetric rotor have the form
\[E_{JK}=\frac{J(J+1)}{2I_{b}}+(\frac{1}{2I_{a}}-\frac{1}{2I_{b}})K^2\; \; J=0,1,2...\; \;\; K=0\pm 1,\pm2,...\pm J\label{41}\]
There is, in addition, the (2J + 1)-fold M degeneracy.
Electronic Excitations in Diatomic Molecules
The quantum states of molecules are composites of rotational, vibrational and electronic contributions. The energy spacing characteristic of these different degrees of freedom vary over many orders of magnitude, giving rise to very different spectroscopic techniques for studying rotational, vibrational and electronic transitions. Electronic excitations are typically of the order of several electron volts, 1 eV being equivalent to approximately 8000 cm-1 or 100 kJ mol-1. As we have seen, typical energy differences are of the order of 1000 cm-1 for vibration and 10 cm-1 for rotation. Fig. 6 gives a general idea of the relative magnitudes of these energy contributions. Each electronic state has a vibrational structure, characterized by vibrational quantum numbers v and each vibrational state has a rotational structure, characterized by rotational quantum numbers J and M.
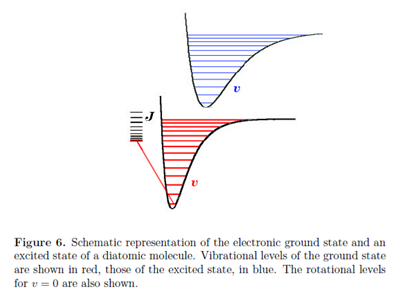
Every electronic transition in a molecule is accompanied by changes in vibrational and rotational states. Generally, in the liquid state, individual vibrational transitions are not resolved, so that electronic spectra consist of broad bands comprising a large number of overlapping vibrational and rotational transitions. Spectroscopy on the gas phase, however, can often resolve individual vibrational and even rotational transitions.
When a molecule undergoes a transition to a different electronic state, the electrons rearrange themselves much more rapidly than the nuclei. To a very good approximation, the electronic state can be considered to occur instantaneously, while the nuclear configuration remains fixed. This is known as the Franck-Condon principle. It has the same physical origin as the Born-Oppenheimer approximation, namely the great disparity in the electron and nuclear masses. On a diagram showing the energies of the ground and excited states as functions of internuclear distance, Franck-Condon behavior is characterized by vertical transitions, in which R remains approximately constant as the molecule jumps from one potential curve to the other.
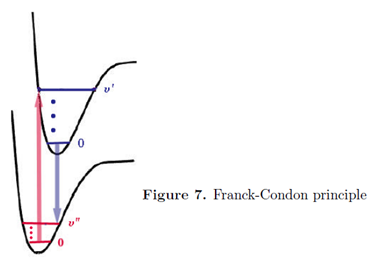
In a vibrational state \(\upsilon \) = 0 the maximum of probability for the internuclear distance R is near the center of the potential well. For all higher values vibrational states, maxima of probability occur near the two turning points of the potential-where the total energy equals the potential energy. These correspond on the diagrams to the end points of the horizontal dashes inside the potential curve.
Contributors and Attributions
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)

