WavePackets
- Page ID
- 38834
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)De Broglie's explanation of the Bohr atom quantization rules, together with the accidental discovery of electron diffraction scattering by Davisson and Germer, make a very convincing case for the wave nature of the electron. Yet the electron certainly behaves like a particle sometimes. An electron has a definite mass and charge, it can move slowly, it can travel through a piece of apparatus from a gun to a screen. What, then, is the relationship between the wave and particle viewpoints? De Broglie himself always felt both were always present. He called the wave a pilot wave, and thought it guided the motion of the particle. Unfortunately, that viewpoint leads to contradictions. The standard modern interpretation is that the intensity of the wave (measured by the square of its amplitude) at any point gives the relative probability of finding the particle at that point. This interpretation, originally presented by Max Born in 1926, is parallel to the relation between the electromagnetic field and quanta -- the probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of the magnetic field vector. The standard notation for the de Broglie wave function associated with the electron is \(\psi (x,t)\). Thus, \(|\psi (x,t)|^2\Delta x\) is the relative probability of finding the electron in a small interval of length \(\Delta x\) near point \(x\) at time \(t\). (For the moment, we restrict the electron to move in one dimension for simplicity. The generalization is straightforward.)
Keeping the Wave and the Particle Together?
Suppose following de Broglie we write down the relation between the "particle properties" of the electron and its "wave properties":
\[\dfrac{mv^2}{2} = E = h\nu \label{1a}\]
\[mv = p = \dfrac{h}{\lambda} \label{1b}\]
It would seem that we can immediately figure out the speed of the wave, just using \(\lambda \nu = v\), say. We find:
\[ \lambda \nu = \left(\dfrac{h}{mv} \right) \times \left(\dfrac{mv^2}{2h} \right) = \dfrac{v}{2} \label{2}\]
So the speed of the wave seems to be only half the speed of the electron! How could they stay together? What's wrong with this calculation?
Localizing an Electron
To answer this question, it is necessary to think a little more carefully about the wave function corresponding to an electron traveling through a vacuum tube, say. The electron leaves the cathode, shoots through the vacuum, and impinges on an anode of a grid. At an intermediate point in this process, it is moving through the vacuum and the wave function must be nonzero over some volume, but zero in the places the electron has not possibly reached yet, and zero in the places it has definitely left.
However, if the electron has a precise energy, say fifty electron volts, it also has a precise momentum. This necessarily implies that the wave has a precise wavelength. But the only wave with a precise wavelength \(\lambda\) has the form
\[\psi(x,t)= A\sin(kx-\omega t) \label{3}\]
where \(k = 2\pi /\lambda\), and \(\omega = 2\pi \nu\). The problem is that this plane sine wave extends to infinity in both spatial directions, so cannot represent a particle whose wave function is non zero in a limited region of space.
Therefore, to represent a localized particle, we must superpose waves having different wavelengths. The principle is best illustrated by superposing two waves with slightly different wavelengths, and using the trigonometric addition formula:
\[ \sin [(k-\Delta k)x - (\omega - \Delta \omega)t] + \sin [(k+\Delta k)x -(\omega + \Delta \Omega)t]= \]
\[ \sin (kx - \omega t) \cos [(\Delta k)x - (\Delta \omega) t ] \label{4}\]
This formula represents the phenomenon of beats between waves that are close in frequency. The first term, \(\sin(kx-\omega t)\), oscillates at the average of the two frequencies. It is modulated by the slowly varying second term, which oscillates once over a spatial extent of order \(\frac{\pi}{\Delta k}\). This is the distance over which waves initially in phase at the origin become completely out of phase. Of course, going a further distance of order \(\frac{\pi }{\Delta k}\), the waves will become synchronized again.
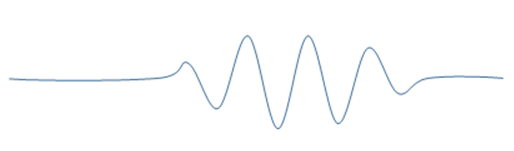
That is, beating two close frequencies together breaks up the continuous wave into a series of packets, the beats. To describe a single electron moving through space, we need a single packet. This can be achieved by superposing waves having a continuous distribution of wavelengths, or wave numbers within of order \(\Delta k\), say of \(k\). In this case, the waves will be out of phase after a distance of order \(\frac{\pi}{\Delta k}\), but since they have many different wavelengths, they will never get back in phase again.
The Uncertainty Principle
It should be evident from the above argument that to construct a wave packet representing an electron localized in a small region of space, the component waves must get out of phase rapidly. This means their wavelengths cannot be very close together. In fact, it is not difficult to give a semi-quantitative estimate of the spread in wavelength necessary, just from a consideration of the two beating waves.
A packet localized in a region of extent \(\Delta x\) can be constructed of waves having k's spread over a range \(\Delta k\), where \(\Delta x ~ \dfrac{\pi}{\Delta k}\).
Now, \(k = 2\pi /\lambda\), and \(p = \dfrac{h}{\lambda}\), so \(k = 2\pi \dfrac{p}{h}\).
Therefore the uncertainly of \(k\) can be expanded
\[\Delta k = 2\pi \dfrac{\Delta p}{h} \label{5a}\]
and
\[\Delta x ~ \dfrac{p}{\Delta k} \approx \dfrac{h}{\Delta p} \label{5b}\]
(ignoring the factor of 2 for now).
Thus:
\[\Delta x \Delta p \approx h \label{6}\]
This is Heisenberg's Uncertainty Principle.
Reconciling the "conflicting" Wave/Particle Properties
Establishing that an electron moving through space must be represented by a wave packet also resolves the paradox that the velocity of the waves seems to be different from the velocity of the electron. The point is that the electron waves, like water waves but unlike electromagnetic waves, have differing phase and group velocities. To see this, consider again the beating of two waves of slightly different wavelengths in Equation \(\ref{4}\).
The waves described by the term \(\sin(kx - \omega t)\) have velocity \(½v\), as previously derived. However, the envelope, the shape of the wave packet, has velocity \(\frac{\Delta \omega}{\Delta k}\) rather than \(\frac{\omega}{k}\). These velocities would be the same if \(\omega\) were linear in \(k\), as it is for ordinary electromagnetic waves. However, the \(\omega - k\) relationship follows from the energy-momentum relationship for the (non-relativistic) electron:
\[E = \dfrac{mv^2}{2} = \dfrac{p^2}{2m}. \label{7}\]
So
\[\dfrac{dE}{dp} = \dfrac{p}{m} = v. \label{8}\]
Equations \(\ref{7}\) and \(\ref{8}\) address the particle nature, but considering the wave nature:
\[E = h\nu = \dfrac{h\omega}{2pi}\label{9}\]
and
\[p = \dfrac{h}{\lambda} = \dfrac{hk}{2\pi}. \label{10}\]
Therefore,
\[\dfrac{\Delta \omega}{\Delta k} = \dfrac{dE}{dp} = v \label{11}\]
So the packet travels at the speed we know the electron must travel at, even though the wave peaks within the packet travel at one-half the speed.
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)

