Fractional Distillation of Non-ideal Mixtures (Azeotropes)
- Page ID
- 78268
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Positive Deviation from Raoult's Law
Remember that a large positive deviation from Raoult's Law produces a vapor pressure curve with a maximum value at some composition other than pure A or B. If a mixture has a high vapor pressure it means that it will have a low boiling point. The molecules are escaping easily and you won't have to heat the mixture much to overcome the intermolecular attractions completely. The implication of this is that the boiling point / composition curve will have a minimum value lower than the boiling points of either A or B.
In the case of mixtures of ethanol and water, this minimum occurs with 95.6% by mass of ethanol in the mixture. The boiling point of this mixture is 78.2°C, compared with the boiling point of pure ethanol at 78.5°C, and water at 100°C. You might think that this 0.3°C doesn't matter much, but it has huge implications for the separation of ethanol / water mixtures. The next diagram shows the boiling point / composition curve for ethanol / water mixtures. I've also included on the same diagram a vapor composition curve in exactly the same way as we looked at on the previous pages about phase diagrams for ideal mixtures.
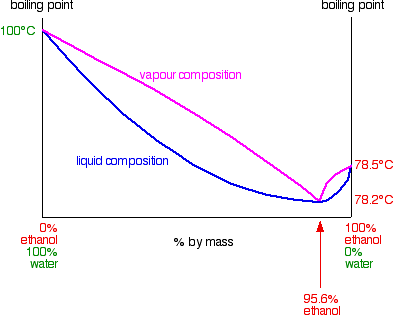
Suppose you are going to distil a mixture of ethanol and water with composition C1 as shown on the next diagram. It will boil at a temperature given by the liquid curve and produce a vapor with composition C2.
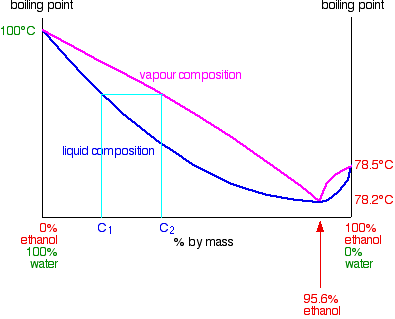
When that vapor condenses it will, of course, still have the composition C2. If you reboil that, it will produce a new vapor with composition C3.
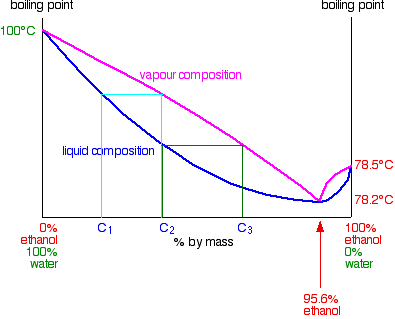
You can see that if you carried on with this boiling-condensing-reboiling sequence, you would eventually end up with a vapor with a composition of 95.6% ethanol. If you condense that you obviously get a liquid with 95.6% ethanol.
What happens if you reboil that liquid? The liquid curve and the vapor curve meet at that point. The vapor produced will have that same composition of 95.6% ethanol. If you condense it again, it will still have that same composition. You have hit a barrier. It is impossible to get pure ethanol by distilling any mixture of ethanol and water containing less than 95.6% of ethanol. This particular mixture of ethanol and water boils as if it were a pure liquid. It has a constant boiling point, and the vapor composition is exactly the same as the liquid. It is known as a constant boiling mixture or an azeotropic mixture or an azeotrope.
The implications of this for fractional distillation of dilute solutions of ethanol are obvious. The liquid collected by condensing the vapor from the top of the fractionating column cannot be pure ethanol. The best you can produce by simple fractional distillation is 95.6% ethanol. What you can get (although it isn't very useful!) from the mixture is pure water. As ethanol rich vapor is given off from the liquid boiling in the distillation flask, it will eventually lose all the ethanol to leave just water.
To Summarize
Distilling a mixture of ethanol containing less than 95.6% of ethanol by mass lets you collect:
- a distillate containing 95.6% of ethanol in the collecting flask (provided you are careful with the temperature control, and the fractionating column is long enough);
- pure water in the boiling flask.
What if you distil a mixture containing more than 95.6% ethanol? Work it out for yourself using the phase diagram, and starting with a composition to the right of the azeotropic mixture. You should find that you get:
- a distillate containing 95.6% of ethanol in the collecting flask (provided you are careful with the temperature control and the fractionating column is long enough);
- pure ethanol in the boiling flask.
A negative deviation from Raoult's Law
Nitric acid and water form mixtures in which particles break away to form the vapor with much more difficulty than in either of the pure liquids. You can see this from the vapor pressure / composition curve discussed further up the page. That means that mixtures of nitric acid and water can have boiling points higher than either of the pure liquids because it needs extra heat to break the stronger attractions in the mixture.
In the case of mixtures of nitric acid and water, there is a maximum boiling point of 120.5°C when the mixture contains 68% by mass of nitric acid. That compares with the boiling point of pure nitric acid at 86°C, and water at 100°C. Notice the much bigger difference this time due to the presence of the new ionic interactions (see above). The phase diagram looks like this:
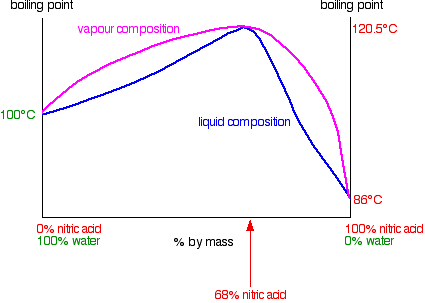
Distilling dilute nitric acid. Start with a dilute solution of nitric acid with a composition of C1 and trace through what happens.
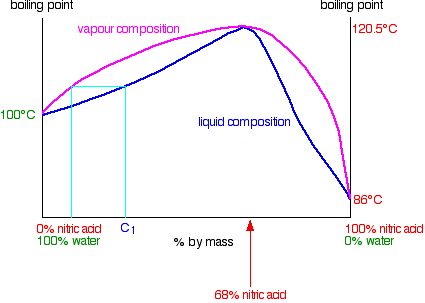
The vapor produced is richer in water than the original acid. If you condense the vapor and reboil it, the new vapor is even richer in water. Fractional distillation of dilute nitric acid will enable you to collect pure water from the top of the fractionating column. As the acid loses water, it becomes more concentrated. Its concentration gradually increases until it gets to 68% by mass of nitric acid. At that point, the vapor produced has exactly the same concentration as the liquid, because the two curves meet. You produce a constant boiling mixture (or azeotropic mixture or azeotrope) and if you distil dilute nitric acid, that's what you will eventually be left with in the distillation flask. You cannot produce pure nitric acid from the dilute acid by distilling it.
You cannot produce pure nitric acid from the dilute acid (<68%) by distilling it.
Distilling nitric acid more concentrated than 68% by mass
This time you are starting with a concentration C2 to the right of the azeotropic mixture.
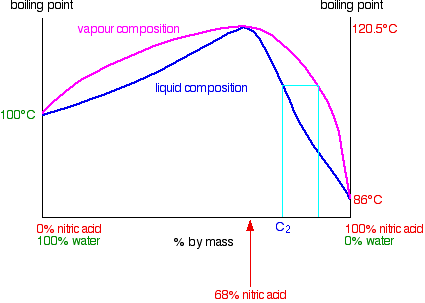
The vapor formed is richer in nitric acid. If you condense and reboil this, you will get a still richer vapor. If you continue to do this all the way up the fractionating column, you can get pure nitric acid out of the top. As far as the liquid in the distillation flask is concerned, it is gradually losing nitric acid. Its concentration drifts down towards the azeotropic composition. Once it reaches that, there cannot be any further change, because it then boils to give a vapor with the same composition as the liquid. Distilling a nitric acid / water mixture containing more than 68% by mass of nitric acid gives you pure nitric acid from the top of the fractionating column and the azeotropic mixture left in the distillation flask.
You can produce pure nitric acid from the concetrated acid (>68%) by distilling it.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


