Immiscible Liquids and Steam Distillation
- Page ID
- 3871
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page looks at systems containing two immiscible liquids. Immiscible liquids are those which won't mix to give a single phase. Oil and water are examples of immiscible liquids - one floats on top of the other. It explains the background to steam distillation and looks at a simple way of carrying this out.
The vapor pressure of mixtures of immiscible liquids
Obviously if you have two immiscible liquids in a closed flask and keep everything still, the vapor pressure you measure will simply be the vapor pressure of the one which is floating on top. There is no way that the bottom liquid can turn to vapor. The top one is sealing it in. For the purposes of the rest of this topic, we always assume that the mixture is being stirred or agitated in some way so that the two liquids are broken up into drops. At any one time there will be drops of both liquids on the surface. That means that both of them contribute to the overall vapor pressure of the mixture.
Total vapor pressure of the mixture
Assuming that the mixture is being agitated, then both of the liquids will be in equilibrium with their vapors. The total vapor pressure is then simply the sum of the individual vapor pressures:
\[\text{Total vapor pressure} = p_A^o + p_B^o\]
where \(p^o\) refers to the saturated vapor pressure of the pure liquid. Notice that this is independent of the amount of each sort of liquid present. All you need is enough of each so that both can exist in equilibrium with their vapor.
For example, phenylamine and water can be treated as if they were completely immiscible. (That isn't actually true, but they are near enough immiscible to be usable as an example.)
At 98°C, the saturated vapor pressures of the two pure liquids are:
| phenylamine | 7.07 kPa |
| water | 94.30 kPa |
The total vapor pressure of an agitated mixture would just be the sum of these - in other words, 101.37 kPa
Boiling point of the mixture
Liquids boil when their vapor pressure becomes equal to the external pressure. Normal atmospheric pressure is 101.325 kPa. Compare that with the figure we have just got for the total vapor pressure of a mixture of water and phenylamine at 98°C. Its total vapor pressure is fractionally higher than the normal external pressure. This means that such a mixture would boil at a temperature just a shade less than 98°C - in other words lower than the boiling point of pure water (100°C) and much lower than the phenylamine (184°C).
Exactly the same sort of argument could be applied to any other mixture of immiscible liquids. I've chosen the phenylamine-water mixture just because I happen to have some figures for it!
Important conclusion
Agitated mixtures of immiscible liquids will boil at a temperature lower than the boiling point of either of the pure liquids. Their combined vapor pressures are bound to reach the external pressure before the vapor pressure of either of the individual components get there.
Steam distillation
Notice that in the presence of water, phenylamine (or any other liquid which is immiscible with water) boils well below its normal boiling point. This has an important advantage in separating molecules like this from mixtures. Normal distillation of these liquids would need quite high temperatures. On the whole these tend to be big molecules we are talking about. Quite a lot of molecules of this sort will be broken up by heating at high temperatures. Distilling them in the presence of water avoids this by keeping the temperature low. That's what steam distillation achieves.
We will carry on with the phenylamine example for now. During the preparation of phenylamine it is produced as a part of a mixture containing a solution of all sorts of inorganic compounds. It is removed from this by steam distillation.
Steam is blown through the mixture and the water and phenylamine turn to vapor. This vapor can be condensed and collected.
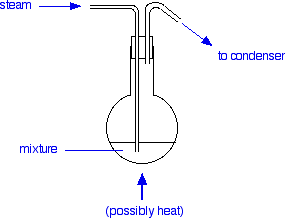
The steam can be generated by heating water in another flask (or something similar). As the hot steam passes through the mixture it condenses, releasing heat. This will be enough to boil the mixture of water and phenylamine at 98°C provided the volume of the mixture isn't too great. For large volumes, it is better to heat the flask as well to avoid having to condense too much steam and increase the volume of liquid in the flask too much.
The condensed vapor will consist of both water and phenylamine. If these were truly immiscible, they would form two layers which could be separated using a separating funnel. In fact, the phenylamine has a slight solubility in water and various other techniques have to be used in this particular case to get the maximum yield of phenylamine. These aren't relevant to this topic.
Some other applications of steam distillation
Steam distillation can be used to extract some natural products - for example, to extract eucalyptus oil from eucalyptus, citrus oils from lemon or orange peel, and to extract oils used in perfumes from various plant materials.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


