Liquid-Solid Phase Diagrams: Salt Solutions
- Page ID
- 3867
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page looks at the phase diagram for mixtures of salt and water - how the diagram is built up, and how to interpret it. It includes a brief discussion of solubility curves.
Two Typical Solubility Curves
A solubility curve shows how the solubility of a salt like sodium chloride or potassium nitrate varies with temperature. The solubility is often (although not always) measured as the mass of salt which would saturate 100 grams of water at a particular temperature. A solution is saturated if it will not dissolve any more of the salt at that particular temperature - in the presence of crystals of the salt.
For most, but not all, substances, solubility increases with temperature. For some (like potassium nitrate), the increase is quite fast. For others (like sodium chloride), there is only a small change in solubility with temperature.
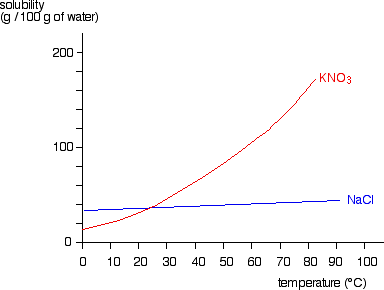
Obviously, a solubility curve shows you the solubility of a substance at a particular temperature. For phase diagram purposes, one important way of looking at this is to examine what happens if you decrease the temperature of a solution with some given concentration. For example, suppose you have a near-boiling solution of potassium nitrate in water. We'll take a solution containing 100 g of potassium nitrate and 100 g of water. Now let the solution cool.

At all temperatures above that marked on the graph (about 57°C), 100 g of water will dissolve more than 100 g of potassium nitrate. All the potassium nitrate will stay in solution.
At 57°C, you hit the solubility curve. This is the temperature at which 100 g of water will dissolve 100 g of potassium nitrate to give a saturated solution. If the temperature falls even the tiniest bit below 57°C, the water will no longer dissolve as much potassium nitrate - and so some crystallises out. The lower the temperature falls, the more potassium nitrate crystallizes, because the water will dissolve less and less of it.
You can think of this as a simple phase diagram. If you have a mixture of 100 g of potassium nitrate and 100 g of water and the temperature is above 57°C, you have a single phase - a solution of potassium nitrate. If the temperature is below 57°C for this mixture, you will have a mixture of two phases - the solution and some solid potassium nitrate. The solubility curve represents the boundary between these two different situations. We'll look now at the phase diagram for sodium chloride solution in some detail.
The phase diagram for sodium chloride solution
We'll talk through what everything means in detail, but first of all notice two things compared with the similar tin-lead phase diagram I hope you have already read about.
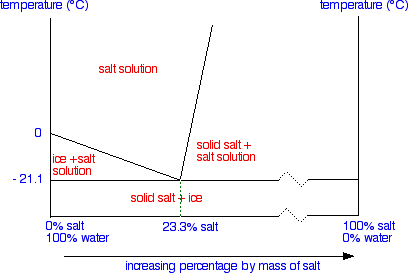
First we are only looking at a very restricted temperature range. The top of this particular diagram is only about 50°C - although it could go higher than that. Secondly, all the action takes place in the left-hand side of the diagram. That's why a lot of the horizontal scale is missing (represented by the broken zigzag in the scale).
The labeled areas in the phase diagram
These areas all show what you would see if you had a particular mixture of salt and water at a given temperature. For example, if the temperature was below -21.1°C, you would always see a mixture of solid salt and ice. There would never be any liquid whatever proportions of salt and water you had. At temperatures above this, what you would see would depend on where your particular set of conditions fell in the diagram. You just need to notice what area the conditions fall into.
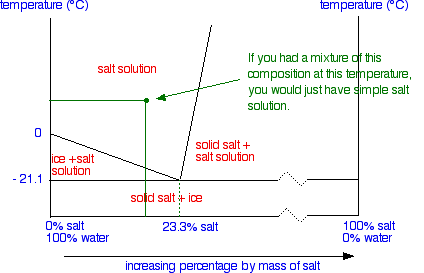
What the lines mean
Let's take the lines one at a time. The first one to look at is the one in bold green in the next diagram.

This line represents the effect of increasing amounts of salt on the freezing point of water. Up to the point where there is 23.3% of salt in the mixture, the more salt the lower the freezing point of the water. The second line is actually a solubility curve for salt in water - although it doesn't look quite like the one we described earlier on this page.

The reason that it looks different is because the axes have been reversed. On a normal solubility curve, temperature is the horizontal axis and the vertical axis shows the solubility in grams per 100 g of water - a measure of concentration.
This time the measure of concentration is the horizontal axis and temperature the vertical one.
If you have already read about the tin-lead system, you might think it strange to include a solubility curve in the phase diagram. In the tin-lead system, both of the sloping lines showed the effect of one of the components on the freezing point of the other. But if you think what this means, it isn't so odd.
The freezing point is the temperature at which crystals start to appear when you cool a liquid mixture. In the case of a salt solution with concentrations of salt greater than 23.3%, the solubility curve shows the temperature at which crystals of salt will appear when you cool a solution of a given concentration. If you aren't clear about that, go back and re-read the beginning of this page.
There is also a hidden difference between this line and the corresponding line on the tin-lead diagram. In that case, both of the sloping lines eventually reached the the left-hand or the right-hand axis. It was possible to talk about the case where you had 100% lead or 100% tin. In this case it is impossible to get to 100% salt. This line eventually comes to an end. At 1 atmosphere pressure it won't get very far above 100°C because the water will boil and you won't have a solution any more.
Even if you raise the pressure, the maximum temperature you could achieve would be 374°C - the critical temperature of the water. Water doesn't exist as a liquid above this temperature. To get to the right-hand side of the graph where you have 100% salt, you would have to get the temperature up to 801°C - the melting point of the salt.
After all this hassle, the final line is easy!
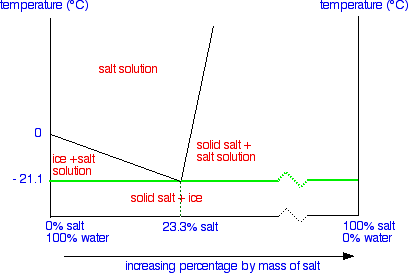
This line is simply drawn across at the lowest temperature at which a mixture of salt and water can contain any liquid. This is known as the eutectic temperature. The particular mixture of salt and water (containing 23.3% salt) which freezes at this temperature is known as a eutectic mixture.
Using Phase Diagrams
The phase diagram is used to find out what happens if you cool salt solution of a particular concentration. We need to look at three separate cases.
Cooling salt solution with the eutectic composition
This is the easy one!
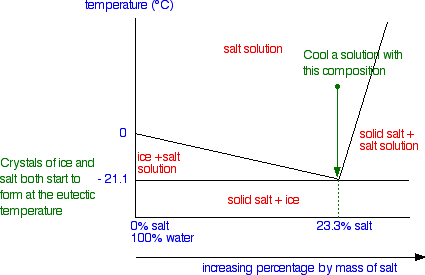
Nothing happens until you get down to the eutectic temperature. At that point, you will start to get both ice crystals and salt crystals forming. If you keep cooling it, you will obviously end up with a solid mixture of ice and salt. You are moving straight from the "salt solution" area of the phase diagram into the "solid salt + ice" area.
Cooling salt solution more dilute than the eutectic composition
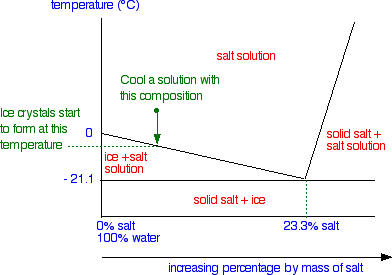
When the temperature drops enough so that it reaches the boundary between the two areas of the phase diagram, ice crystals start to form - in other words, the solution starts to freeze. As the solution continues to cool, it moves down into the "ice + salt solution" region. Obviously, the composition of the solution has changed because it contains less water - some of it has frozen to give ice. But the composition of the system as a whole is still the same, and so we continue down the same line.
To find out what is actually in the mixture, you draw a horizontal tie line through the point showing the temperature you have got to, and look at what it hits at either end.
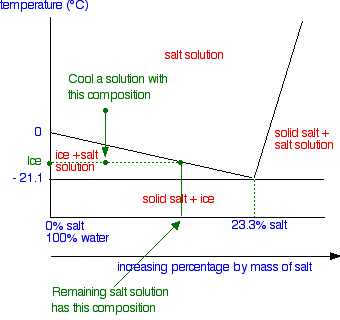
- On the left it hits the vertical axis showing 100% water - in this case, that's the pure ice crystals.
- On the other end, it hits the sloping line - this tells you the composition of the remaining salt solution.
As the mixture continues to cool, it will eventually reach the eutectic temperature, and at this point all of the rest of the solution will turn to solid - a mixture of ice and salt crystals.
Cooling salt solution more concentrated than the eutectic composition
The phase diagram is interpreted in just the same way - except that this time, salt crystals are formed at first rather than ice crystals. In the next diagram, the first salt crystals will form when the temperature hits the boundary line. As the temperature continues to drop into the "solid salt + salt solution" area, more and more salt will crystallize out. To find out exactly what is present at any temperature, you can again draw a tie line and look at what is at either end.
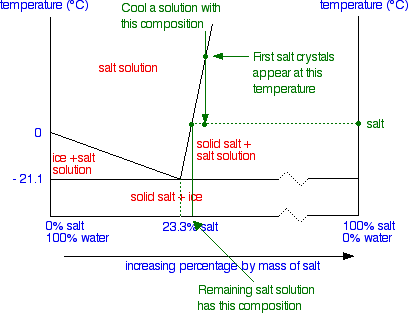
The diagram shows the tie line when the temperature has dropped to some random place in the "solid salt + salt solution" area. Again, by looking at the ends of this tie line, you can see that the mixture contains solid salt (the 100% salt at the right-hand end of the line) and a solution whose concentration can be found by looking at the left-hand end of the line. As the temperature continues to fall, you will eventually reach the eutectic temperature, when everything left - salt and water - will turn to solid giving you a mixture of solid salt and ice.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


