10.2: Energy Minimization - Four Methods Using Mathcad
- Page ID
- 135896
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Using \( \psi ( \alpha , r) = \frac{ \alpha ^{3}}{ \pi} exp( - \alpha r)\) as a trial wave function for the helium atom electrons leads to the following energy expression in terms of the variational parameter, α.
\( E( \alpha ) = \alpha ^{2} - 4 \alpha + \frac{5}{8} \alpha\)
The first term is electron kinetic energy, the second electron‐nucleus potential energy and the final term electron‐electron potential energy.
Mathcad provides four methods for energy minimization with respect to \(α\). The second and third methods require a seed value for \(α\).
First method
\[ \alpha = \frac{d}{d \alpha} E( \alpha ) = 0 |_{float, 5}^{solve, \alpha} \rightarrow 1.6875 \nonumber \]
\( E ( \alpha ) = -2.8477\)
Second method
α = 1. Given \( \frac{d}{d \alpha} E ( \alpha ) = 0\) \( \alpha = Find ( \alpha )\) α = 1.685 \( E ( \alpha ) = -2.8477\)
Third method
α = 1. α : = Minimize(E, α) α = 1.685 \( E ( \alpha ) = -2.8477\)
Fourth method
Clear memory of α and X: α = α Z = Z
\( En ( \alpha ,~Z) = \alpha ^{2} - 2 Z \alpha + \frac{5}{8} \alpha\) \( \frac{d}{d \alpha} En( \alpha ,~Z) = 0~solve, \alpha \rightarrow Z - \frac{5}{16}\)
\( En ( \alpha ,~Z) = \alpha ^{2} - 2 Z \alpha + \frac{5}{8}~substitute, \alpha = Z - \frac{5}{16} \rightarrow - \frac{(16 Z - 5)^{2}}{256}\)
\( En ( \alpha ,~2) = -2.8477\) \( En \alpha ,~3) = -7.2227\) \( En( \alpha ,~4) = -13.5977\)
Two variables: a molecular orbital calculation yields the following result for the energy of the hydrogen molecule ion as a function of the internuclear separation and the orbital decay constant.
\( 1s_{a} = \frac{ \alpha ^{3}}{ \pi} exp(- \alpha r_{a})\)
\( 1s_{b} = \frac{ \alpha ^{3}}{ \pi} exp(- \alpha r_{b})\)
\( S_{ab} = \int 1s_{a} 1s_{b} d \tau\)
\( \psi_{mo} = \frac{1s_{a} + 1s_{b}}{ \sqrt{2+2 S_{ab}}}\)
\[ E( \alpha, R) = \frac{- \alpha^{2}}{2} + \frac{[ \alpha^{2} - \alpha - \frac{1}{R} + \frac{1 + \alpha R}{R} exp(-2 \alpha R) + \alpha ( \alpha - 2) (1+ \alpha R) exp(- \alpha R)]}{[1 + exp(- \alpha R) (1+ \alpha R + \frac{ \alpha^{2} R^{3}}{3})]} + \frac{1}{R} \nonumber \]
α = 1 R = 1 \( \begin{pmatrix}
\alpha \\
R
\end{pmatrix}\) = Minimize(E, α, R) \( \begin{pmatrix}
\alpha \\
R
\end{pmatrix}\) = \( \begin{pmatrix}
1.2380 \\
2.0033
\end{pmatrix}\) E(α, R) = -0.5865
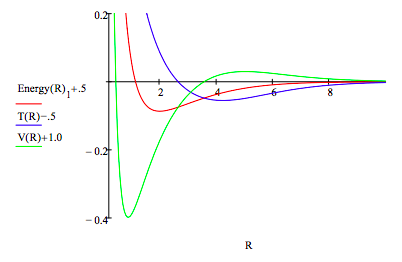
α = 1 Energy = -2 Given Energy = E(α, R) \( \frac{d}{d \alpha}\) E(α, R) = 0 Energy(R) = Find(α, Energy)
R = .2, .25 .. 10 T(R) = -Energy(R)1 - R \( \frac{d}{dR}\) Energy(R)1 V(R) = 2 \( \) Energy(R)1 + R \( \frac{d}{dR}\) Energy(R)1