1.84: A Brief Tutorial on Wavepackets
- Page ID
- 157648
“A wavepaccket is a superposition of wavefunctions that is usually strongly peaked in one region of space and virtually zero elsewhere. The peak of the wavepacket denotes the most likely location of the particle; it occurs where the contributing wavefunctions are in phase and interfere constructively. Elsewhere the wavefunctions interfere destructively, and the net amplitude is small or zero.
A wavepacket moves because all the component functions change at different rates, and at different times the point of maximum constructive interference is in different locations. The motion of the wavepacket corresponds very closely to the motion predicted for a classical particle in the same potential. An important difference from classical physics is that the wavepacket spreads with time, but this tendency is very small for massive, slow particles.” P. W. Atkins, Quanta, page 395.
The time dependent coordinate-space wavefunction for a free particle with momentum p is, in atomic units:
\[
\begin{array}{l}{\mathrm{m} :=1 \qquad \mathrm{p} :=1} \qquad {\mathrm{x} :=-10,-9.95 \ldots 10}\end{array} \\ \Psi_{\mathrm{p}}(\mathrm{x}, \mathrm{t}) :=\frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \exp \left(\frac{-\mathrm{i} \cdot \mathrm{p}^{2} \cdot \mathrm{t}}{2 \cdot \mathrm{m}}\right) \quad \text{where} \quad \mathrm{E}_{\mathrm{p}}=\frac{\mathrm{p}^{2}}{2 \mathrm{m}}
\nonumber \]
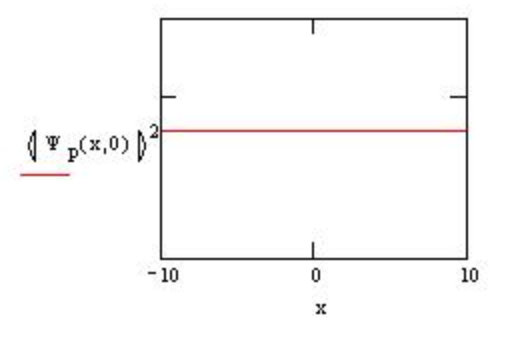
In quantum mechanics a state such as this with a precisely known momentum must have a completely uncertain position as is shown in the graph above for p=1. To use this wavefunction to model a particle it is necessary to form a linear superposition of momentum states. This adds enough uncertainty to momentum to localize the position of the particle to some degree. Because the momentum of a free particle is a continuous variable the discrete summation is replaced by the integral summation in forming the linear superpositon.
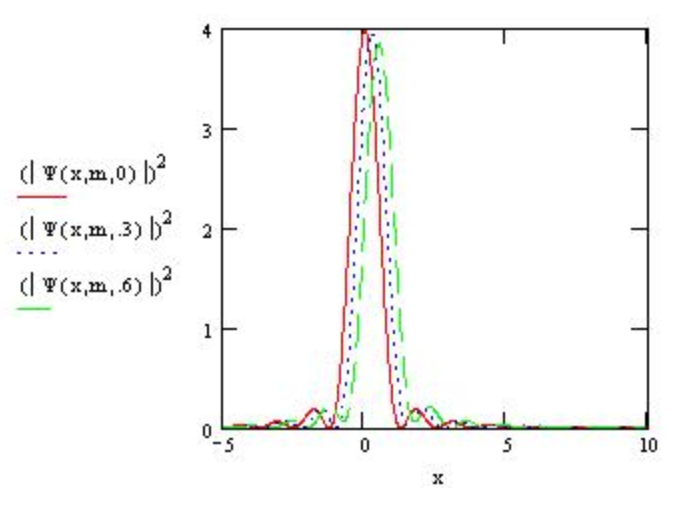
For example, the wavefunction for a particle of mass =1 moving to right with momentum between 5 and 10 atomic units is calculated below and the probability distribution is plotted for several times. Note that the wavepacket is indeed spreading as Atkins said it would.
\[
\mathrm{m} :=1 \qquad \mathrm{x} :=-5,-4.98 \ldots 10 \\ \Psi (x,m,t) : = \frac{1}{\sqrt{2 \cdot \pi}} \int_{5}^{10} \exp \left[i \cdot \left(p \cdot x - \frac{p^{2} \cdot t}{2 \cdot m}\right)\right]dp
\nonumber \]
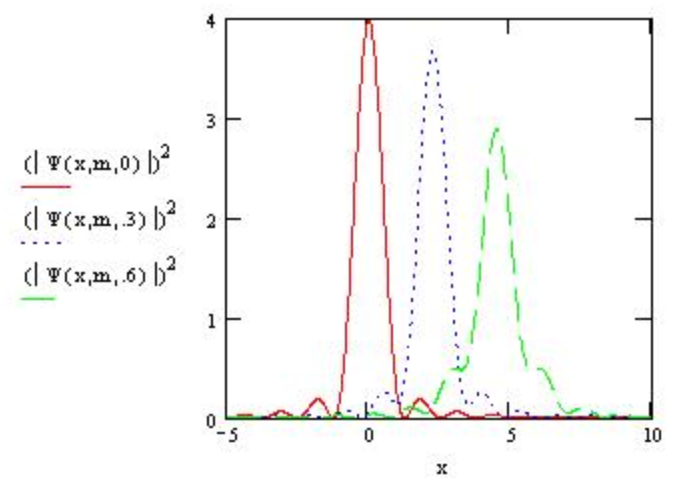
The spreading is not as great for more massive particles as can be seen by increasing the mass to 3.
\[m : = 3 \nonumber \]
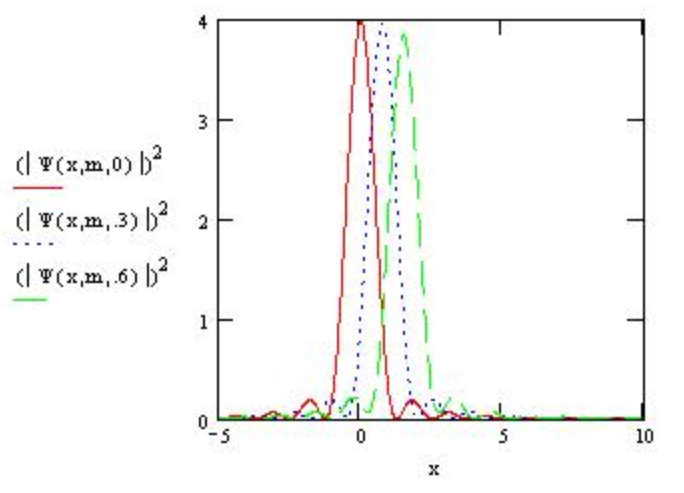
Atkins also said the spreading is not as great for slower participles. This is shown below by summing momentum values from 0 to 5 instead of 5 to 10.
\[
\Psi(x, m, t) :=\frac{1}{\sqrt{2 \cdot \pi}} \int_{0}^{5} \exp \left[i \cdot\left(p \cdot x-\frac{p^{2} t}{2 \cdot m}\right)\right] d p
\nonumber \]