1.31: The Position and Momentum Commutation Relation in Coordinate and Momentum Space
- Page ID
- 143938
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The purpose of this exercise is to illustrate the commutation relation between position and momentum in the coordinate and momentum representations using a one‐dimensional representation of the hydrogen atom. The relevance of the uncertainty principle to these calculations will also be demonstrated. All calculations are done in atomic units: e = me = \(4 \pi \epsilon_{o} = \frac{h}{2 \pi}\) = 1.
Coordinate Representation
| Position operator: \(x \cdot \Box\) | Momentum operator: \(p=\frac{1}{i} \cdot \frac{d}{d x} \Box\) | Integral: \( \int_{0}^{\infty} \Box d x\) | Kinetic energy operator: \( K E=-\frac{1}{2} \cdot \frac{d^{2}}{d x^{2}} \Box\) | Potential energy operator: \(P E=\frac{-1}{x}\) |
The 1s state of the hydrogen can be represented in one‐dimension by the following wave function:
\[
\Psi(x)=2 \cdot x \cdot \exp (-x) \qquad \int_{0}^{\infty} \Psi(x)^{2} d x \rightarrow 1
\nonumber \]
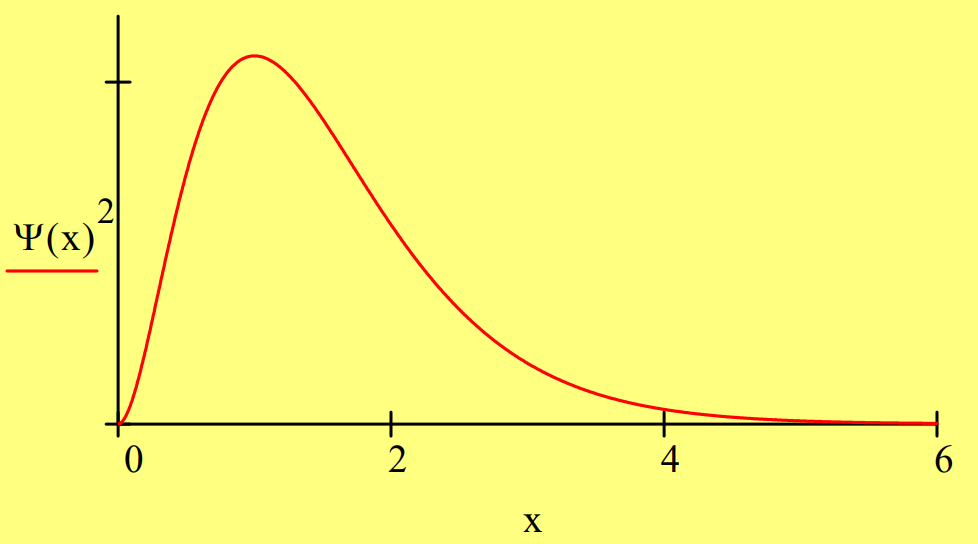
First we demonstrate that \(\Psi\)(x) is an eigenfunction of the energy operator with eigenvalue ‐0.5 in atomic units.
\[
\frac{-\frac{1}{2} \cdot \frac{d^{2}}{d x^{2}} \Psi(x)-\frac{1}{x} \cdot \Psi(x)}{\Psi(x)} \rightarrow \frac{-1}{2}
\nonumber \]
It is easy to show that \(\Psi (x)\) is not an eigenfunction of the position or momentum operators. This means that while the electron in the hydrgogen atom ground state has a well‐defined energy, it does not have a well‐defined position or momentum. This fact is consistent with the commutator and uncertainty calculations shown below.
Next it is shown that the position and momentum operators do not commute.
\[
\frac{x \cdot\left(\frac{1}{i} \cdot \frac{d}{d x} \Psi(x)\right)-\frac{1}{i} \cdot \frac{d}{d x}(x \cdot \Psi(x))}{\Psi(x)} \text { simplify } \rightarrow i
\nonumber \]
This result indicates that \(\Psi (x)\) is not an eigenstate of the position and momentum operators, and therefore the order of measurement is important. Gaining knowledge of one observable through measurement destroys information about the other. The commutation relation is closely related to the uncertainty principle, which states that the product of uncertainties in position and momentum must equal or exceed a certain minimum value, 0.5 in atomic units.
The uncertainties in position and momentum are now calculated to show that the uncertainty principle is satisfied.
\[
\Delta x :=\sqrt{\int_{0}^{\infty} \Psi(x) \cdot x^{2} \cdot \Psi(x) d x-\left(\int_{0}^{\infty} \Psi(x) \cdot x \cdot \Psi(x) d x\right)^{2}} \rightarrow \frac{1}{2} \cdot 3^{\frac{1}{2}}
\nonumber \]
\[
\Delta p :=\sqrt{\int_{0}^{\infty} \Psi(x) \cdot \frac{d^{2}}{d x^{2}} \Psi(x) d x-\left(\int_{0}^{\infty} \Psi(x) \cdot \frac{1}{i} \cdot \frac{d}{d x} \Psi(x) d x\right)^{2}} \rightarrow 1
\nonumber \]
\[
\Delta x \cdot \Delta p=0.866
\nonumber \]
We now move to momentum space to show that the results are identical to those calculate in coordinate space.
Momentum Representation
| Position operator: \(i \cdot \frac{d}{dp} \Box\) | Momentum operator: \(p \cdot \Box\) | Momentum space integral: \(\int_{-\infty}^{\infty} \Box d p\) |
A momentum wave function is obtained by a Fourier transform of the coordinate wave function.
\[
\Phi(\mathrm{p}) :=\frac{1}{\sqrt{2 \cdot \pi}} \cdot \int_{0}^{\infty} \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \Psi(\mathrm{x}) \mathrm{dx} \text { simplify } \rightarrow \frac{2^{\frac{1}{2}}}{\pi^{\frac{1}{2}} \cdot(\mathrm{i} \cdot \mathrm{p}+1)^{2}}
\nonumber \]
\[
\int_{-\infty}^{\infty}(|\Phi(p)|)^{2} d p \rightarrow 1
\nonumber \]
The coordinate and momentum wave functions are equivalent representations of the hydrogen‐atom ground state. That they contain the same information as is illustrated below.
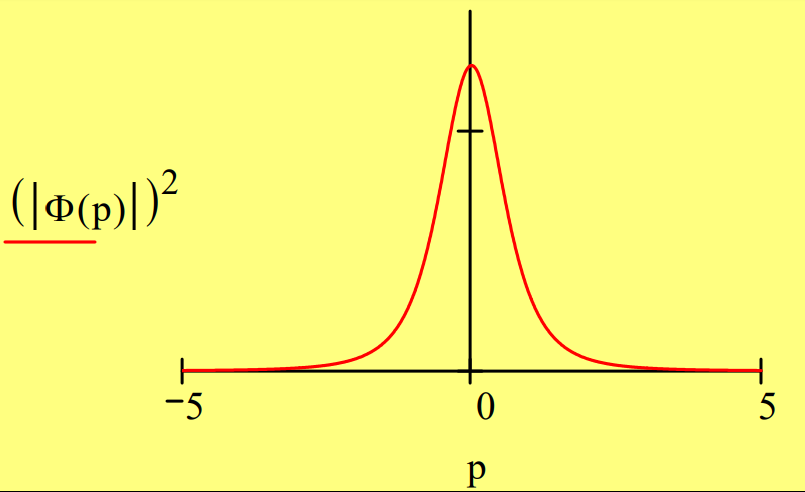
The position and momentum operators do not commute in momentum space.
\[
\frac{\mathrm{i} \cdot \frac{\mathrm{d}}{\mathrm{dp}}(\mathrm{p} \cdot \Phi(\mathrm{p}))-\mathrm{p} \cdot \mathrm{i} \cdot \frac{\mathrm{d}}{\mathrm{dp}} \Phi(\mathrm{p})}{\Phi(\mathrm{p})} \text { simplify } \rightarrow \frac{-(\mathrm{p}-\mathrm{i})}{\mathrm{i} \cdot \mathrm{p}+1}
\nonumber \]
It is easy to show that this result is equal to i.
The product of the position‐momentum uncertainty is the same in momentum space as it is in coordinate space.
\[
\Delta \mathrm{p} :=\sqrt{\int_{-\infty}^{\infty} \mathrm{p}^{2} \cdot(|\Phi(\mathrm{p})|)^{2} \mathrm{d} \mathrm{p}-\left[\int_{-\infty}^{\infty} \mathrm{p} \cdot(|\Phi(\mathrm{p})|)^{2} \mathrm{d} \mathrm{p}\right]^{2}} \rightarrow 1
\nonumber \]
\[
\Delta x :=\sqrt{\int_{-\infty}^{\infty} \overline{\Phi(p)} \cdot -\frac{d^{2}}{d p^{2}} \Phi(p) d p-\left[\int_{-\infty}^{\infty} \overline{\Phi(p)} \cdot i \cdot\left(\frac{d}{d p} \Phi(p)\right) d p \right]^{2}} \rightarrow \frac{1}{2} \cdot 3^{\frac{1}{2}}
\nonumber \]
\[
\Delta \mathrm{x} \cdot \Delta \mathrm{p}=0.866
\nonumber \]

