1.32: Simulating the Aharonov-Bohm Effect

Last updated
Save as PDF

Page ID: 143947

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Aharonov–Bohm effect is a phenomenon by which an electron is affected by the vector potential, A, in regions in which both the magnetic field B, and electric field E are zero. The most commonly described case occurs when the wave function of an electron passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being zero in the region through which the particle passes.

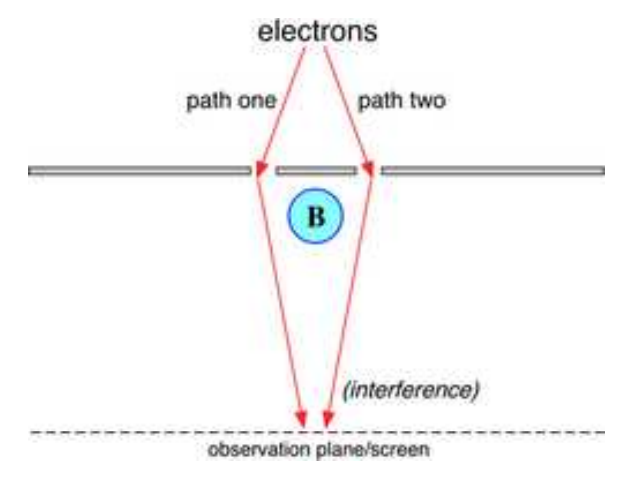
Schematic of double-slit experiment in which Aharonov–Bohm effect can be observed: electrons pass through two slits, interfering at an observation screen, with the interference pattern shifted when a magnetic field B is turned on in the cylindrical solenoid. (All of the above adapted from Wikipeida)

The effect on the interference fringes is calculated and displayed below. Please consult other tutorials on the double-slit interference effect on my page for background information.

Slit positions: \(x_{L} : = 1 \quad x_{R} : = 2\)

Slit width: \(\delta : = 0.2\)

Relative phase shift: \(\phi : = \pi\)

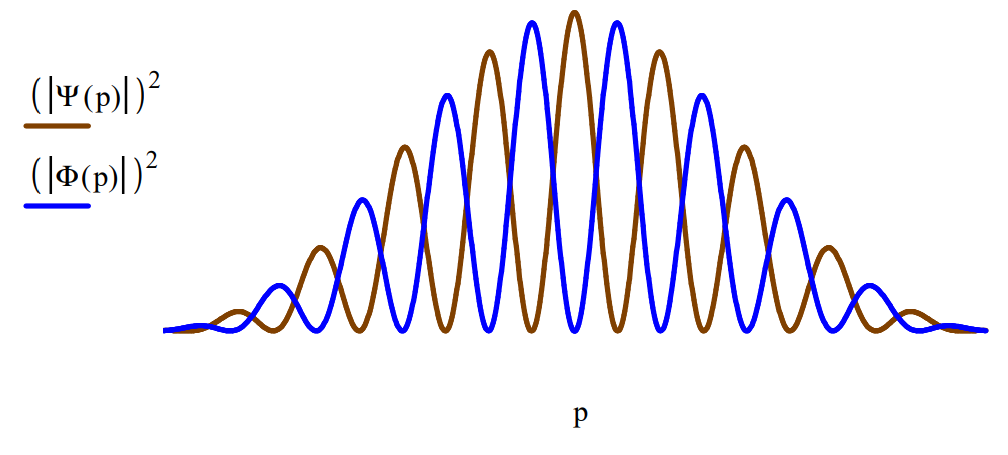
Momentum Distribution/Diffraction Pattern for B = 0:

\[
\Psi(p) :=\frac{1}{\sqrt{2}}\left(\int_{x_{L}-\frac{\delta}{2}}^{x_{L}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x+\int_{x_{R}-\frac{\delta}{2}}^{x_{R}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x\right)
\nonumber \]

Relative phase shift, \(\phi\), introduced at right-hand slit for B not equal to zero:

\[
\Phi(\mathrm{p}) :=\frac{1}{\sqrt{2}}\left(\int_{\mathrm{x}_{\mathrm{L}}-\frac{\delta}{2}}^{\mathrm{x}_{\mathrm{L}}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}+\exp (\mathrm{i} \cdot \phi) \cdot \int_{\mathrm{x}_{\mathrm{R}} +\frac{\delta}{2}}^{\mathrm{x}_{\mathrm{R}}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} \right)
\nonumber \]

Display both diffraction patterns: