1.24: Getting Accustomed to the Superposition Principle
- Page ID
- 143931
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is impossible to simulate a quantum mechanical superposition with a mixture of M&M candies, or any other ensemble of macroscopic objects (1). Among the defining characteristics of a superposition is that it is not a mixture. Miller acknowledges that while his demonstration is not "strictly accurate", it is "quite effective and achieves a variety of educational goals." In spite of Miller's claims it is my contention that the students have not been provided with a concrete or correct picture of the superposition principle with his exercise.
Here is what Dirac had to say about the linear superposition in his famous treatise on quantum mechanics:
The nature of the relationships which the superposition principle requires to exist between the states of any system is of a kind that cannot be explained in terms of familiar physical concepts. One cannot in the classical sense picture a system being partly in each of two states and see the equivalence of this to the system being completely in some other state. There is an entirely new idea involved, to which one must get accustomed and in terms of which one must proceed to build up an exact mathematical theory, without having any detailed classical picture. (2)
With regard to the desire for classical pictures, Dirac said,
...the main object of physical science is not the provision of pictures, but is the formulation of laws governing phenomena and application of these laws to the discovery of new phenomena. If a picture exists, so much the better; but whether a picture exists or not is a matter of only secondary importance. In the case of atomic phenomena no picture can be expected to exist in the usual sense of the word 'picture' by which is meant a model functioning essentially on classical lines. (3)
We do more harm than good by constructing facile, but false classical analogies for non-classical concepts. Therefore, the only reliable way to get accustomed to the non-classical nature of the quantum mechanical superposition is by direct appeal to experiment. One must study those cases in optics and spectroscopy, for example, where the superposition principle manifests itself most directly. The available examples are edifying, plentiful, and usually quite surprising.
Before reviewing some of these experimental examples I would like to comment on two errors in Miller's application of the superposition principle to the particle in a one-dimensional box. First, he incorrectly writes that the wave function is \(\Psi(x) :=N \cdot \sin (n \cdot k \cdot x)\), but clearly the argument of the sine function is either (knx) or \(\frac{n \pi x}{a}\)), where a is the box dimension. This initial error is compounded by the assertion that the coordinate-space wave function is an equal superposition of two momentum eigenstates with eigenvalues "proportional" (?) to \(\frac{kh}{2 \pi}\). Basically the same error is made by Atkins (4), Miller's primary reference.
The expectation value for momentum is indeed zero, but to describe in more detail the outcome of momentum measurements on a particle in a one-dimensional box a momentum-space wave function is required. Such a wave function can be obtained by a Fourier transform of the coordinate-space wave function into momentum space (5, 6, 7). For the particle in a one-bohr box, in atomic units, the Fourier transform is,
\[
\Phi(\mathrm{p}) :=\frac{1}{\sqrt{2 \cdot \pi}} \cdot \int_{0}^{1} \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \sqrt{2} \cdot \sin (\mathrm{n} \cdot \pi \cdot \mathrm{x}) \mathrm{d} \mathrm{x}
\nonumber \]
Evaluation of this integral yields,
\[
\Phi(\mathrm{p}) :=\frac{\mathrm{n} \cdot \pi-\mathrm{n} \cdot \exp (-\mathrm{i} \cdot \mathrm{p}) \cdot \cos (\mathrm{n} \cdot \mathrm{p})-\mathrm{i} \cdot \mathrm{p} \cdot \exp (-\mathrm{i} \cdot \mathrm{p}) \cdot \sin (\mathrm{n} \cdot \pi)}{\sqrt{\pi} \cdot\left(\mathrm{n}^{2} \cdot \pi^{2}-\mathrm{p}^{2}\right)}
\nonumber \]
Graphical representations of the momentum-space distribution, \(|\Phi(\mathrm{p})|^{2}\), as a function of the quantum number n demonstrate that the momentum distribution is never simply \(\frac{kh}{2 \pi}\) (5, 6, 7).
Turning now to empirical examples of the superposition principle, we consider first the double-slit experiment which Richard Feynman made so famous.
We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by "explaining" how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics. (8)
Amplifying the last sentence of this quotation Feynman said, at another time, the double-slit experiment is so fundamental that if asked a question about quantum mechanics one can always reply, "You remember the case of the experiment with the two holes? It's the same thing." (9)
The salient feature of all double-slit experiments is, as shown in Fig. 1, that between source (S) and detector (D) the particle is offered two paths (P1, P2).
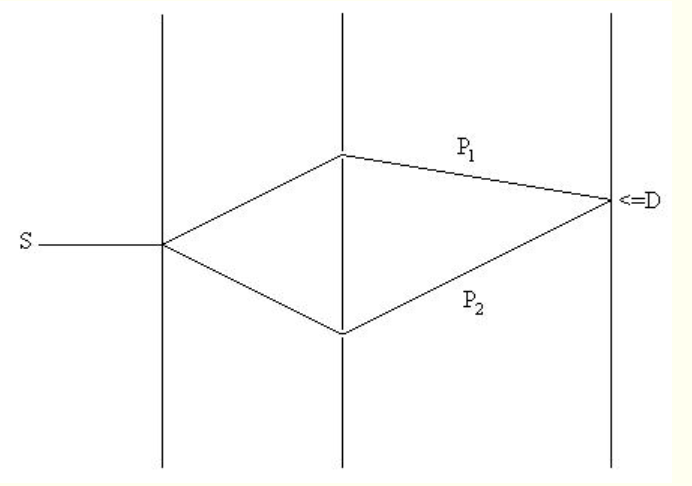
Fig. 1 - Schematic diagram of the double-slit experiment. S = source; D = detector; P1 = path 1; P2 = path 2.
If the path of the particle is not observed quantum mechanics requires its wave function to be a linear superposition of arriving at D by taking both paths. Under these circumstances, the probability that a particle leaving S will be detected at D is calculated as the absolute square of the sum of the probability amplitudes for arriving at D via P1and P2. (10)
\[
P(S \rightarrow D)=|\langle D| S\rangle\left.\right|^{2}=|\langle D| P_{1}\rangle\langle P_{1}|S\rangle+|\langle D\left|P_{2}\rangle\langle P_{2}\right| S\rangle\left.\right|^{2}
\nonumber \]
Calculation of the double-slit interference pattern is straightforward (11). The probability amplitude for reaching the detector via P1, for example, is proportional to \(\frac{\exp \left(\frac{2 \pi i \delta_{1}}{\lambda}\right) }{ \delta_{1}}\), where \(\lambda\) is the de Broglie wavelength of the particle and \(\delta_{1}\) is the distance between source and detector via P1. Substitution of this expression and a similar one for P2 into the previous equation yields,
\[P(S, D) : = \left[ \left| \frac{\exp \left(2 \cdot \pi \cdot i \cdot \frac{\delta_{1}}{\lambda}\right)}{\delta_{1}} + \frac{\exp \left(2 \cdot \pi \cdot i \cdot \frac{\delta_{2}}{\lambda}\right)}{\delta_{2}} \right| \right]^{2} \nonumber \]
The addition of probability amplitudes before squaring (rather than squaring the individual probability amplitudes) leads to interference effects, a signature of the linear superposition, and one of its essential features that Miller's mixtures of M&Ms can't capture.
While Feynman presented the double-slit example pedagogically as a 'thought experiment' in his text, it has ample empirical verification for a variety of particles. For example, a demonstration of the double-slit experiment involving single electrons (only one electron in the apparatus at a time) has been reported in the pedagogical literature (12). Quite recently a striking interference pattern has been observed for C60 in a multi-slit apparatus using a diffraction grating. C60 is the most massive particle, so far, to demonstrate the wave-particle duality underlying the double-slit experiment (13). Very recently a temporal double-slit experiment with attosecond windows in the time domain has been reported. 13a
The results reported above, and those that will follow, are stunning examples of quantum mechanical behavior with roots deep in the superposition principle. In these experiments the source produces particles and the detector registers particles, but between source and detector the behavior is wave-like with the particle apparently traversing both paths simultaneously. In light of this bizarre behavior Feynman said,
I think I can safely say that nobody understands quantum mechanics... Do not keep saying to yourself, if you can possibly avoid it, 'But how can it be like that?' because you will 'get down the drain', into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that. (9)
I think Feynman's comment, delivered in his well-known colloquial style, carries the same message as the more formal statements by Dirac quoted earlier. Dirac and Feynman are saying we must get accustomed to the fact that the nano-world is not simply a miniature of the macro-world. We must resist the expectation of being able to employ naive, visually-based, classical concepts in the nanoscopic realm. When we can't resist, we fail and then blame quantum theory for being abstract and remote from experience. However, our blame is misplaced as Marvin Chester points out in the following quotation.
The mathematical predictions of quantum mechanics yield results that are in agreement with experimental findings. That is the reason we use quantum theory. That quantum theory fits experiment is what validates the theory, but why experiment should give such peculiar results is a mystery." (14)
We continue with manifestations of the superposition principle using an example from chemistry. Chemical reactions that occur by more than one mechanism create the possibility, under favorable circumstances, of a chemical double-slit phenomena with accompanying interference effects. This is how Dixon, et al. (15) have recently interpreted some unusual results in the photo-dissociation of water. The reaction H2O + h\(\nu\) ---> H + OH can occur through two linear intermediates I1 (HOH), and I2 (HHO). The OH moiety has a relative 180o phase difference in the two intermediates, which leads to an observed even-odd intensity oscillation in the rotational states of the product OH. For the transition from reactants (R) to products (P) by a two-intermediate mechanism the previous equation becomes,
\[
\mathrm{P}(\mathrm{R} \rightarrow \mathrm{P})=|\langle\mathrm{P}| \mathrm{R}\rangle\left.\right|^{2}= |\langle\mathrm{P}| \mathrm{I}_{1}\rangle\langle\mathrm{I}_{1}|\mathrm{R}\rangle+|\langle\mathrm{P}\left|\mathrm{I}_{2}\rangle\langle\mathrm{I}_{2}\right| \mathrm{R}\rangle\left.\right|^{2} =|\Psi\left(I_{1}\right)+(-1)^{N} \Psi\left.\left(I_{2}\right)\right|^{2}
\nonumber \]
where N is the rotational quantum number and the term (-1)N takes into account that even rotational states are symmetric with respect to a 180o rotation, while odd rotational states are anti-symmetric to such rotations. Clearly the interference term in this equation will be alternatively positive and negative, in agreement with the spectroscopic data.
Perhaps the most simple and striking version of the double-slit experiment is single-photon interference performed with a Mach-Zehnder interferometer (16). This apparatus, as Fig. 2 shows, consists of a photon source S, two 50-50 beam splitters BS, two mirrors M, and two detectors, D1 and D2.
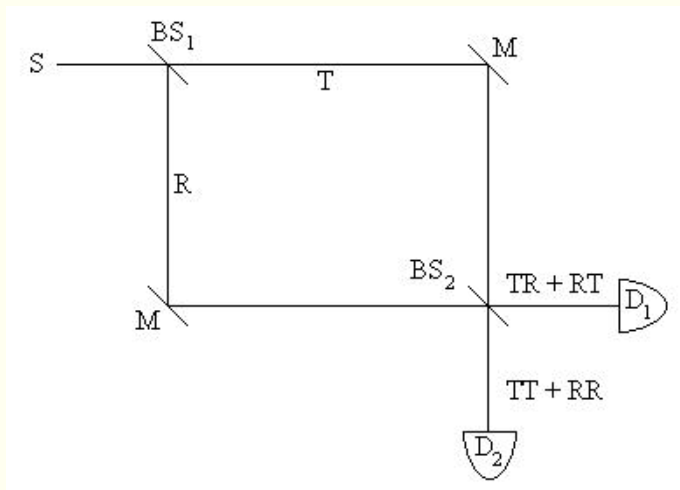
Fig. 2 - Schematic diagram of a Mach-Zehnder interferometer. S = source; BS = beam splitter; M = mirror; R = reflected; T = transmitted; D = detector; TT = transmitted at BS1 and transmitted at BS2; TR = transmitted at BS1 and reflected at BS2; etc.
The experiment can be performed with a low intensity source such that there is only one photon in the interferometer at any time. With equal path lengths to the detectors, the photon is always detected at D1. Each detector can be reached by both paths and this requires the addition of probability amplitudes for each path, just as in the previous examples.
For D1 the amplitudes are in phase and for D2 they are 180 out of phase, so the photon is never detected at D2. At the beam splitters the probability amplitude for transmission is 2-1/2 (= 0.707), while for reflection it is i 2-1/2 (= 0.707 i). A 90o phase difference between transmission and reflection at the beam splitters (17, 18) is assigned by convention to the reflected beam. The probability for the arrival of a photon at D1 or D2is calculated using the same formalism as in the previous examples.
\[
\left|\langle D_{1}\right| S\rangle\left.\right|^{2}=\left|\langle D_{1}\right| I\rangle\langle T|S\rangle+|\langle D_{1}|R \times R| S\rangle\left.\right|^{2} =|(0.707 i)(0.707)+ (0.707)\left.(0.707 i)\right|^{2}=1
\nonumber \]
\[
\left|\langle D_{2}\right| S\rangle\left.\right|^{2}=\left|\langle D_{2}\right| I\rangle\langle T|S\rangle+|\langle D_{2}|R \times R| S\rangle\left.\right|^{2} =|(0.707)(0.707)+ (0.707i)\left.(0.707 i)\right|^{2}=0
\nonumber \]
If either path is blocked 50% of the photons get through, and 25% reach D1 and 25% reach D2. If the second beam splitter is removed 50% of the photons are detected at D1and 50% at D2. In both cases there is only one path to each detector, so there is no opportunity for interference of probability amplitudes.
In the examples presented so far particles have been described as being in a linear superposition of having taken both paths, not a mixture of some particles taking one path and some taking the other. The evidence in favor of the superposition has been interference effects, something which doesn't occur with mixtures of particles. However, it is possible to distinguish superpositions from mixtures without observing interference.
This example will treat Stern-Gerlach measurements in the x-z plane on spin-\(\frac{1}{2}\) particles (19). Spin in the x- and z-directions are incompatible observables because their associated operators do not commute, which means that they cannot have simultaneous eigenstates. If a particle has a well-defined spin in the z-direction, its spin in the x-direction is uncertain, and vice versa. There are two eigenstates for each spin direction.
Let's say they are \(| \uparrow \rangle\) and \(| \downarrow \rangle\) in the z-direction, and \(| \rightarrow \rangle\) and \(| \leftarrow \rangle\) in the x-direction. The incompatibility of these observables is expressed by the following superpositions, which may also be expressed in vector form (19).
\[
| \uparrow \rangle=\frac{1}{\sqrt{2}}[ |\rightarrow\rangle+| \leftarrow \rangle ] \qquad | \downarrow \rangle=\frac{1}{\sqrt{2}}[ |\rightarrow\rangle-| \leftarrow \rangle ]
\nonumber \]
\[
| \rightarrow \rangle=\frac{1}{\sqrt{2}}[ |\uparrow\rangle+| \downarrow \rangle ] \qquad | \leftarrow \rangle=\frac{1}{\sqrt{2}}[ |\uparrow\rangle-| \downarrow \rangle ]
\nonumber \]
Now suppose that a beam of spin-\(\frac{1}{2}\) particles is passed through a Stern-Gerlach apparatus oriented in the z-direction. A statistically meaningful number of measurements yields 50% \(| \uparrow \rangle\) and 50% \(| \downarrow \rangle\). Two hypotheses that are consistent with this outcome will be considered: the beam of particles could be completely un-polarized in the x-z plane, a random mixture of \(| \uparrow \rangle\), \(| \downarrow \rangle\), \(| \rightarrow \rangle\), and \(| \leftarrow \rangle\); or it could be a linear superposition, \(| \uparrow \rangle \pm | \downarrow \rangle\). To distinguish between these alternatives it is only necessary to rotate the Stern-Gerlach magnet so that it is oriented along the x-direction. If the beam is an un-polarized mixture a large number of measurements will yield 50% \(| \rightarrow \rangle\) and 50% \(| \leftarrow \rangle\). However, if it is a linear superposition of \(| \uparrow \rangle\) and \(| \downarrow \rangle\), by the equations shown above, it will yield either 100% \(| \rightarrow \rangle\) or 100% \(| \leftarrow \rangle\). Experiments of this type have been reported in the primary literature (20) and summarized in the review literature (21).
Another example of the importance of the linear superposition is the ammonia maser which was first achieved experimentally in 1953. In an early paper on the maser in the popular scientific literature, J. P. Gordon (22) correctly described it as a "quantum-mechanical device." The maser is based on the ammonia molecule's umbrella inversion which in the classical view the nitrogen atom oscillates "back and forth" through the plane of the hydrogen atoms. This inversion vibration can be modeled quantum mechanically by a dominant harmonic potential supplemented with an internal Gaussian barrier which creates the required double potential well (23).
\[
\mathrm{V}=\frac{1}{2} \mathrm{k} \mathrm{x}^{2}+\mathrm{b} \exp \left(-\mathrm{c} \mathrm{x}^{2}\right)
\nonumber \]
The presence of the internal barrier causes a bunching of adjacent symmetric (+) and anti-symmetric (-) harmonic oscillator states. All states are raised in energy by the presence of the barrier, but the (-) states are elevated less than the (+) states because they have a node in the barrier and the (+) states do not. Thus v = 0 and v = 1, v = 2 and v = 3, etc. become paired with the effect declining in importance with increasing v quantum number as the magnitude of the energy barrier becomes less significant.
The ammonia maser is based on a microwave transition involving the first pair of symmetric and anti-symmetric states, v = 0 and v = 1. Numerical integration of Schrödinger's equation (24) for the first two states yields the wave equations shown in Fig. 3.
Fig. 3 - First two states ( v = 0 and v = 1) for the harmonic oscillator with an internal Gaussian barrier. The wave functions are off-set on the vertical axis for clarity of presentation.
Clearly these states represent in-phase and out-of-phase superpositions of the nitrogen atom being on both sides of the plane of the hydrogen atoms. If |NH3> represents the left-hand well and |H3N> the right-hand well, we can write the wave functions for these states symbolically as shown below.
\[
|\Psi\rangle_{0}=2^{-1 / 2}\left[\mathrm{NH}_{3}\rangle+| \mathrm{H}_{3} \mathrm{N}\rangle\right] \quad \text{and} \quad | \Psi\rangle_{1}=2^{-1 / 2}\left[\left|\mathrm{NH}_{3}\rangle-\right| \mathrm{H}_{3} \mathrm{N}\rangle\right]
\nonumber \]
The energy difference between these states is only 0.79 cm-1 (23), so they are essentially equally populated at room temperature. However, \(| \Psi \rangle_{1}\) can be separated from \(| \Psi \rangle_{0}\) by electrostatic means and directed to a resonant cavity. Irradiation of the v = 1 state with a 24 GHz signal causes stimulated emission and coherent amplification of the original signal.
Up to this point we have been dealing with "one-particle" superpositions in which a single particle or system is assumed to occupy a linear superposition of two states. However, there is no limit to the number of particles or the number of states involved in the linear superposition. Einstein, in collaboration with Podolsky and Rosen (EPR), was first to explore bizarre implications of the two-particle superposition (25). Schrödinger called this an entangled state and identified it as a fundamental trait of quantum mechanical systems.
For example, suppose that an excited atom (calcium for example) emits two photons in a cascade in opposite directions (26). Conservation of angular momentum requires that the photons are either both right circularly polarized or left circularly polarized. According to the superposition principle the wave function of the composite system must be,
\[
|\Psi \rangle =2^{-1 / 2}\left[\left|\mathrm{R}\rangle_{1}\right| \mathrm{R}\rangle_{2}+\left|\mathrm{L}\rangle_{1}\right| \mathrm{L}\rangle_{2}\right]
\nonumber \]
An EPR-like analysis demonstrated, and experiment confirmed, that such a quantum mechanically entangled state violated the realistic principle of locality and permitted in Einstein's words "spooky action at a distance." Once together, always together, or according to Lucien Hardy, "When two particles are in an entangled state they appear to continue to talk to each other even after they have finished interacting directly." (27) Einstein and his co-authors took this unusual prospect (at that time) as evidence that quantum mechanics was not complete and would ultimately have to be superseded by a more comprehensive theory that did not have its unpleasant non-local characteristics.
The EPR thought experiment, in the light of more recent suggestions by Bohm (28) and the penetrating analysis of Bell (29), has generated a remarkable experimental effort during the last 20 years that has confirmed Einstein's worst fear - "spooky action at a distance" is permitted, at least, in the nano-world (30, 31). The experimental study of the Greenberger-Horne-Zeilinger three-particle entanglement by Pan, et al. (32) is among the latest confirmations of the non-locality inherent in entangled superpositions.
The empirical support for the superposition principle outlined above validates its use for theoretical interpretation. For example, we can use the superposition principle to understand the electronic ground state of the hydrogen atom, which in atomic units is, \(\langle\mathrm{r}|\Psi\rangle=\Psi(\mathrm{r})=\pi^{-1 / 2} exp(-r)\). This equation says that the hydrogen atom's electron is in a weighted superposition of all possible distances, r, from the nucleus. It is not orbiting the nucleus in a circular orbit or an elliptical orbit, it is not moving at all in any ordinary sense. The electron does not execute a classical trajectory within the atom. This is why in quantum mechanics we say the electron is in a stationary state, and why, un-like moving charges, it does not radiate or absorb energy unless it is making a transition from one allowed stationary state to another.
The superposition principle also provides a simple interpretation of the covalent chemical bond. In H2+, for example, at the most rudimentary level of theory, we write the molecular orbital as a linear superposition of the 1s orbitals of the two hydrogen atoms: \(\Psi_{\mathrm{MO}}=2^{-1 / 2}\left(\psi_{1 \mathrm{sa}}+\psi_{1 \mathrm{sb}}\right)\). Adding the probability amplitudes, \(\psi_{1sa}\) and \(\psi_{1sb}\), is equivalent to saying the electron is delocalized over the molecule as a whole, and just as in the hydrogen atom case it is not correct to think of the electron as executing a trajectory or hopping back and forth between the two atoms. Squaring \(\Psi_{MO}\) (the sum of two probability amplitudes) to obtain the probability density yields an interference term, \(2\psi_{1sa}\psi_{1sb}\), which leads to a build-up of charge in the internuclear region. Thus constructive interference associated with an in-phase linear superposition of atomic states provides an understanding of the mechanism of chemical bond formation.
Of course, a linear superposition in which the atomic orbitals are 180o (\(\pi\) radians)out of phase leads to destructive interference (charge depletion in the internuclear region) and an anti-bonding molecular orbital. If the atomic orbitals are 90o \(\frac{\pi}{2}\) radians) out of phase, the interference term disappears yielding a non-bonding molecular orbital. In fact the superposition principle supports a continuum of atomic orbital combinations from in-phase bonding to out-of-phase anti-bonding interactions.
Moving from H2+ to larger molecules of more interest to chemists, we employ the same general procedure by writing a trial molecular orbital as a linear combination of all relevant atomic orbitals (LCAO-MO). Application of the variation method to solve Schrödinger's equation yields a set of optimized cannonical molecular orbitals in which the electron density is delocalized (DMO) over the molecule as a whole. While these DMOs have the most direct experimental support through photo-electron spectroscopy (and are, therefore, also called spectroscopic orbitals), they frequently are not the most useful to the chemist who has found localized electron pairs extremely helpful in understanding chemistry. The superposition principle comes to the rescue of the chemist as a number of excellent articles in this Journal have demonstrated over the years (33, 34, 35, 36, 37, 38). Any linear combination of the cannonical orbitals is also a valid solution to Schrödinger's equation. This is the theoretical justification for hybridizing atomic orbitals and forming localized molecular orbitals (LMOs) from DMOs. The superposition principle also provides a quantum mechanical justification for the use of the schematic, but also very useful, Lewis resonance structures (39).
When quantum mechanical principles are applied to atomic and molecular systems, the result is an explanation of atomic and molecular stability (the emergence of a ground state), and a manifold of quantized energy states for the internal degrees of freedom of the system being studied. Spectroscopy deals with the interaction of electromagnetic radiation with matter, and spectra are, therefore, usually interpreted as manifesting "quantum jumps" between the allowed energy levels. The superposition principle provides, as McMillen clearly showed some years ago in this Journal (40), a simple and serviceable model for the ubiquitous quantum jump.
To illustrate this model we consider an electron in the ground state of a one-dimensional box that is exposed to electromagnetic radiation. Under the influence of this perturbation the electron moves into a state that is a time-dependent linear superposition of the ground state and the manifold of excited states (in atomic units).
\[
\Psi :=c_{1} \cdot \psi_{1} \cdot \exp \left(-i \cdot E_{1} \cdot t\right)+\sum_{n=2}^{\infty} c_{n} \cdot \psi_{n} \cdot \exp \left(-i \cdot E_{n} \cdot t\right)
\nonumber \]
For a transition to occur between the ground state and the first excited state, for example, two conditions must be met according to the model proposed by McMillin. First, the Bohr frequency condition must be satisfied, \(\nu = \frac{E_{2} - E_{1}}{h}\) Second, the electron density represented by the square of the absolute magnitude of the time-dependent linear superposition,
\[
\left|\Psi_{1 \rightarrow 2}\right|^{2}=\left|c_{1} \psi_{1} \exp \left(-i \mathrm{E}_{1} \mathrm{t}\right)+\mathrm{c}_{2} \psi_{2} \exp \left(-i \mathrm{E}_{2} \mathrm{t}\right)\right|^{2}
\nonumber \]
must exhibit oscillating dipole character (41). This latter criterion is the selection rule and provides a mechanism for a coupling between the radiation field of frequency n and the electron density also oscillating with frequency \(\nu\). By comparison the n = 1 to n = 3 transition is forbidden, even if the Bohr frequency condition is satisfied, because the time-dependent superposition of these states does not exhibit oscillating dipole character; the electron density oscillates symmetrically about the center of the box and there is no coupling with the oscillating electromagnetic field (41).
These examples, and others not discussed here (26), show that the linear superposition is indeed a fundamental concept in the nanoscopic world of photons, atoms, and molecules. It has in it "the heart of quantum mechanics" to repeat Feynman's words, but what is its status in our macro-world? If quantum mechanics has universal validity, why don't we find macroscopic examples of the superposition principle? Einstein and Schrödinger answered by saying that quantum theory wasn't universally valid and that it did not present a complete physics for even the nano-world.
As noted previously, Einstein and his collaborators (25) demonstrated that quantum mechanics challenged certain scientific assumptions about the nature of physical reality, in particular calling into question traditional ideas regarding determinism, causality, and locality. Schrödinger formulated his famous 'cat paradox' (42) to demonstrate the absurdity of thinking that quantum mechanics and the superposition principle applied to the macro-world. In this ingenious thought experiment he created an entangled linear superposition which coupled the nano-world to the macro-world. Schrödinger postulated that a cat and a radioactive atom with a half-life of one hour were sealed in a box with a device (diabolical, in his words) that kills the cat if the atom decays. Therefore, after one hour the cat is presumably in an even superposition of being both alive and dead - clearly an absurd outcome from the macroscopic point of view. Furthermore, in order to reconcile quantum theory with macro-reality it is necessary to postulate that opening the box for the purpose of observing the actual state of the cat causes the wave function to "collapse" into one or the other of the equally likely contributions to the linear superposition.
\[
|\Psi>=2^{-1 / 2}[|\text { cat alive }\rangle| \text { atom not decayed }\rangle+|\text { cat dead }\rangle| \text { atom decayed }\rangle]
\nonumber \]
In this thought-experiment Schrödinger exposed a serious conflict between the formalism of quantum theory and our everyday experience, and a significant experimental and theoretical effort to resolve the conflict ensued. At the experimental level researchers have attempted to create mesocopic and macroscopic "cat" states (43 - 45). Theorists, for their part, have put considerable effort into creating a mechanism to explain the "collapse" of the wave function and to delineate the border between the quantum and classical worlds (46). For a recent survey of both experimental and theoretical work in this area the interested reader is directed to reference (26).
In summary, my premise has been that there are no classical analogs for the quantum mechanical superposition. To understand it one must study its experimental manifestations which, fortunately, are numerous at the nanoscopic level. To this end I have provided a brief survey of some of the more well-known empirical examples of the superposition principle. Areas of current research involving the quantum mechanical superposition that have been omitted from this presentation in the interest of brevity include quantum computing, quantum cryptography, and quantum teleportation.
Literature Cited
- Miller, J. B. J. Chem. Educ. 2000, 77, 879.
My critique of Miller's paper is not meant to imply that there are no pedagogically effective classical analogs for quantum mechanical principles. For successful attempts to simulate the superposition principle with macro objects see the following:
- de Barros Neto, B. J. Chem. Educ. 1984, 61, 1044.
- Fleming, P. E. J. Chem. Educ. 2001, 78, 57.
- Dirac, P. A. M. Principles of Quantum Mechanics, 4th ed.; Oxford U. P.: London, 1958, p. 12.
- Ibid., p. 10.
- Atkins, P. W. Physical Chemistry, 6th ed.; Freeman: New York, 1998; p. 316.
- Markley, F. L. Am. J. Phys. 1972, 40, 1545.
- Liang, Y. Q.; Zhang, H; Dardenne, Y. X. J. Chem. Educ. 1995, 72, 148.
- Rioux, F. J. Chem. Educ. 1999, 726, 156. See also,http://www.users.csbsju.edu/~frioux/...b-momentum.htm.
- Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965, p. 1-1.
- Feynman, R. P. The Character of Physical Law; MIT Press: Cambridge, 1967; p. 130.
- Dirac's bra-ket notation is used throughout this paper. Feynman's text, ref 8, is perhaps the most accessible introduction to bra-ket notation. In addition, the author has posted a Dirac notation tutorial at: http://www.users.csbsju.edu/~frioux/dirac/dirac.htm.
- See reference 8 page 3 - 4 and www.users.csbsju. edu/~frioux/two-slit/2slit.htm for an example of how to do this calculation using Mathcad.
- Tonomura, A.; Endo, T.; Matsuda, T.; Kawasaki, T.; Ezawa, H. Am. J. Phys. 1989, 57, 117.
- Arndt. M.; Nairz, O.; Vos-Andreae, J.; Keller, C.; Van der Zouw, G.; Zeilinger, A. Nature, 1999, 401, 680.
- For a description and analysis of the temporal double-slit experiment see http://www.users.csbsju.edu/~frioux/...oral-2slit.pdf and references therein.
- For the short version see http://www.users.csbsju.edu/~frioux/...poral2slit.pdf.
- Chester, M. Primer of Quantum Mechanics; Krieger Publishing Co.:Malabar, FL, 1992.
- Dixon, R. N.; Hwang, D. W.; Yang, X. F.; Harich, S.; Lin, J. J.; Yang. X. Science, 1999, 285, 1249.
- Scarani, V.; Suarez, A. Am. J. Phys. 1998, 66, 718. For additional methods of analysis of single photon interference see:
- Degiorgio, V. Am. J. Phys. 1980, 48, 81.
- Zeilinger, A. Am. J. Phys. 1981, 49, 882.
- Rae, A. I. M. Quantum Mechanics, 3rd ed.; Institute of Physics Publishing, Ltd.: Bristol, 1992, pp 110-115.
- Sumhammer, J.; Badurek, G.; Rauch, H.; Kisko, J.; Zeilinger, A. Phys. Rev. A. 1983. 27, 2523.
- Leggett, A. J. Contemp. Phys. 1984, 25, 583.
- Gordon, J. P. Sci. Amer. 1958, 199(6), 42.
- Swalen, J. D.; Ibers, J. A. J. Chem. Phys. 1962, 36, 1914.
- The numerical integration was carried out using Mathcadwww.users.csbsju.edu/~...er/AMMONIA.pdf. with the integration algorithm described in, Hansen, J. C. JCE: Software 1996, 8C(2).
- Einstein, A.; Podolsky, B.; Rosen, N. Phys. Rev. 1935, 45, 777.
- Greenstein, G.; Zajonc, A. G. The Quantum Challenge; Jones and Bartlett Pub.: Sudbury, 1997, and references cited therein.
- Hardy, L. Contemp. Phys. 1998, 39, 419. For a simple example of two-photon entanglement see: http://www.users.csbsju.edu/~frioux/2photon.htm.
- Bohm, D. Quantum Theory; Prentice-Hall: New York, 1951.
- Bell, J. S. Physics 1964, 1, 195. Reprinted in: Bell, J. S. Speakable and Unspeakable in Quantum Mechanics, Cambridge, U. P.: Cambridge, 1987.
- Aspect, A.; Grangier, P.; Roger, G. Phys. Rev. Lett. 1981, 41, 460.
- Greenberger, D. M.; Horne, M. A.; Zeilinger, A. Phys. Today, 1993, 44(8), 22.
- Pan, J-W.; Bouwmeester, D.; Daniel, M.; Winfurter, H.; Zeilinger, A. Nature2000, 403, 515.
- Cohen, I.; Del Bene, J. J. Chem. Educ. 1969, 46, 487.
- Bernett, W. A. J. Chem. Educ. 1969, 46, 746.
- Hoffman, D. K,; Ruedenberg, K. ; Verkade, J. G. J. Chem. Educ. 1977, 54, 590.
- Liang, M. J. Chem. Educ. 1987, 64, 124.
- Gallup, G. A. J. Chem. Educ. 1988, 65, 671.
- Martin, R. B. J. Chem. Educ. 1988, 65, 668.
- Feynman, R. P.; Leighton, R. B.; Sands, M., op. cit., chapter 15.
- McMillin, D. R. J. Chem. Educ. 1978, 55, 7.
- Rioux, F. JCE: Software 1993, 1D(2). See also: http://www.users.csbsju.edu/~frioux/q-jump/njump.pdf.
- Wheeler, J. A.; Zurek, W. H., Editors. Quantum Theory and Measurement; Princeton, U. P.: Princeton, 1983, pp 152-167.
- Monroe, C.; Meekhof, D. M.; King, B. E.; Wineland, D. J. Science 1996, 272, 1131.
- Friedman, J. R.; Patel, V.; Chen, W.; Tolpygo, S. K.; Lukens, J. E. Nature 2000, 406, 43.
- van der Wal, C., et al. Science 2000, 290, 773. See also:www.sciencemag.org/cgi/conten...l/290/5492/720
- Zurek, W. Phys. Today, 1991, 44(10), 36.

