1.25: The Dirac Delta Function

Last updated
Save as PDF

Page ID: 143933

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Dirac delta function expressed in Dirac notation is: \(\Delta(x - x_1) = \langle x | x_1 \rangle \). The \(\langle x | x_1 \rangle\) bracket is evaluated using the momentum completeness condition. See the Mathematical Appendix for definitions of the required Dirac brackets and other mathematical tools used in the analysis that follows.

\[\langle x | x_{1}\rangle=\int_{-\infty}^{\infty}\langle x | p\rangle\langle p | x_{1}\rangle d p=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \exp (i p x) \exp \left(-i p x_{1}\right) d p=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \exp \left[i p\left(x-x_{1}\right)\right] d p \nonumber \]

Evaluation of this integral over a finite range of momentum values shows that the delta function is small except in the immediate neighborhood of x₁. Integrating from -20 to 20 to reduce computational time shows that < x | x₁= 2> is small except in the area x = 2.

\[\mathrm{x}_{1} =2 \quad \mathrm{x} =0,0 .01 \ldots 4 \quad \operatorname{Dirac}\left(\mathrm{x}, \mathrm{x}_{1}\right) =\frac{1}{2 \cdot \pi} \cdot \int_{-20}^{20} \exp \left[\mathrm{i} \cdot \mathrm{p} \cdot\left(\mathrm{x}-\mathrm{x}_{1}\right)\right] \mathrm{d} \mathrm{p} \nonumber \]

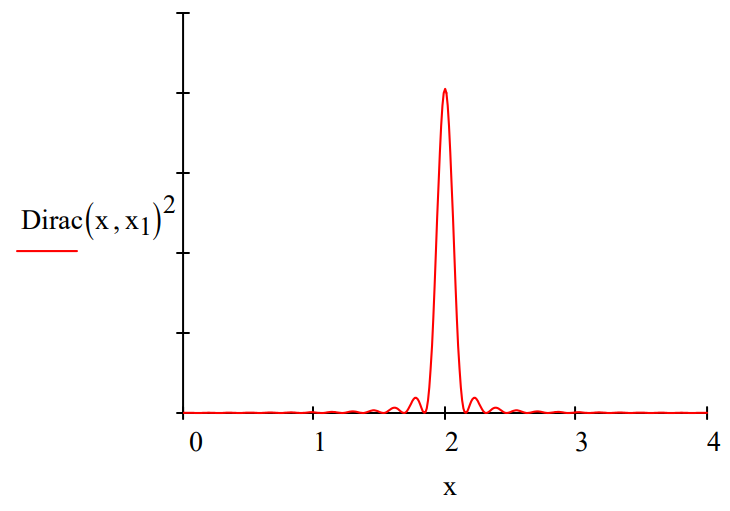
The Fourier transform of the Dirac delta function into the momentum representation yields the following result.

\[
\int_{-\infty}^{\infty}\langle p | x\rangle\langle x | x_{1}\rangle d x=\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{1}\right)=\langle p | x_{1}\rangle
\nonumber \]

The normalization constant is omitted for clarity of expression and the previous value of x₁ is cleared to allow symbolic calculation.

\[
\mathrm{x}_{1} =\mathrm{x}_{1} \qquad \int_{-\infty}^{\infty} \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \Delta\left(\mathrm{x}-\mathrm{x}_{1}\right) \mathrm{d} \mathrm{x} \text { simplify } \rightarrow \; \mathrm{e}^{-\mathrm{p} \cdot \mathrm{x}_{1} \cdot \mathrm{i}}
\nonumber \]

Mathematical Appendix

The position and momentum completeness conditions:

\[
\int | x \rangle\langle x|d x=1 \qquad \int| p\rangle\langle p|d p=1
\nonumber \]

The momentum eigenstate in the coordinate representation:

\[
\langle x | p\rangle=\frac{1}{\sqrt{2 \pi}} \exp (i p x)
\nonumber \]

The position eigenstate in the momentum representation:

\[
\langle p | x\rangle=\frac{1}{\sqrt{2 \pi}} \exp (-i p x)
\nonumber \]