3.E: Exercises

Q3.6

Calculate the work done by the reaction

\[\ce{Zn(s) + H2SO4(aq) → ZnSO4(aq) + H2(g)}\]

when 1 mole of hydrogen gas is collected at 273 K and 1.0 atm. (Neglect volume changes other than the change in gas volume, and assume that the has behaves ideally.)

Q3.11a

If the internal energy of 3 moles of Cl₂ is 3.96 KJ, what is the temperature of the system?

Q3.11b

The internal energy of 3 moles of neon gas (Ne) is 4.87 kJ. Assuming conditions are ideal, what is the temperature of the system?

S3.11b

Since we can assume that conditions are ideal, we know that the temperature is 25°C or 298 K. This assumption allows us to ignore the small change in volume of the gas.

Q3.12a

Some ice cubes are placed inside a sealed plastic bag on a hot day, what is the sign of \(w\), \(q\), \(ΔH\), \(ΔU\)? What does this mean about the system?

Q3.12b

A sports bottle containing Gatorade is held in a man's hand while running on a treadmill. Suppose the Gatorade is the system in question. Answer the subsequent questions.

1. Will the temperature rise due to the movement caused by the man's running?
2. Was any heat actually added to the system? If so, what was the source?
3. Was work done onto the system?
4. In what ways has the internal energy of the system been affected, if affected at all?

S3.12b

1. The man's running motion causes the Gatorade to be shaken. The shaking motion adds energy to the system and increases the random motion of the molecules. Since the motion of the molecules rises, so does the temperature of the system.
2. Yes, heat exchange did occur between the system and its surroundings (the heat given off from the man's hand).
3. Yes, work was done onto the system via the shaking motion.
4. The internal energy has been increased.

Q3.12c

Consider an ice cube melting.

1. Is the change of enthalpy positive or negative for this process?
2. Is the change of entropy positive or negative for this process?

S3.12c

1. Enthalpy is positive because the ice must gain heat in order to melt.
2. Entropy is also positive because the water molecules are gaining kinetic energy and moving to a more disordered state.

Q3.13

2.5 moles of CO₂ expands against an external pressure of 1.5 atm. It was initially at 9.0 atm and 30^ºC. The final volume is 35.0 L.

1. What is the final temperature?
2. Calculate q, w, and \(\Delta U\) for the process.

S3.13

a) \(T=\dfrac{PV}{Rn}= \dfrac{(1.5atm)(35L)}{(.08206\dfrac{L\cdot atm}{mol\cdot K})(2.5 mol)}= 255K\)

b) \(w=-(nRT)ln\dfrac{P_1}{P_2}=-(2.5mol)(8.314\dfrac{J}{mol\cdot K})(255K)ln\dfrac{9.0atm}{1.5atm}=-9.5\dfrac{kJ}{mol}\)

\(q_p=nCpT= n\dfrac{3}{2}RT= (2.5mol)\dfrac{3}{2}(8.314\dfrac{J}{mol\cdot K})(255K)= 7.95\dfrac{kJ}{mol}\)

\(\Delta U=q+w= 7.95\dfrac{kJ}{mol} + -9.5\dfrac{kJ}{mol}= -1.55\dfrac{kJ}{mol}\)

- For calculating work, expression for Isothermal reversible process has been used instead of correct -Pext*dV as it is a irreversible expansion against external pressure. -Wrong method for calculating q. Instead Internal energy would be calculated using nCv*dT.

Q3.17

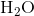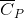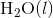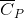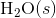Determine the at 343.15 K for . (Note: The heat of vaporization for water is known to be 40.79 kJ mol^-1 at 273.15 K, the of was determined to be 85.6 J K^-1 mol^-1 and the of was determined to be 54.35 J K^-1 mol^-1). Use the reaction below and give your final answer in kJ mol^-1.

S3.17

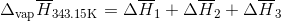
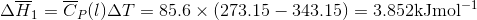
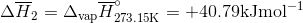
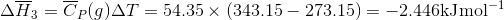
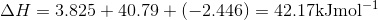
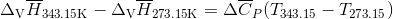
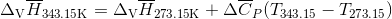
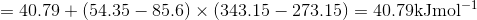
Q3.18

,Is \((q= -w\) true for a cyclic process?

S3.18

Yes, \(q= -w\) is a true statement. It is true because \(\Delta U\) for any cyclic process is equal to zero.

Q3.22

A 10.0 g sheet of gold with a temperature of 18.0°C is laid flat on a sheet of iron that weights 20.0 g and has a temperature of 55.6°C. Given that the specific heats of Au and Fe are 0.129 J g^_-1 °C^-1 and 0.444 J g^_-1 °C^-1, respectively, what is the final temperature of the combined metals? (Hint: The heat gained by the gold must be equal to the heat lost by the iron.)

Q3.23

You are cooking 100 grams of chicken soup at 300K. You know that it will take 500 J to raise the temperature of your soup to the desired 350K. Assuming constant pressure, calculate the molar heat capacity of this chicken soup.

Q3.24

Why does the molar heat of vaporization for water decrease as temperature increases?

Q3.24

The value of ∆H for heating 1 mole of hexane is 28.9kJ/mole at 342 K and 25.6 kJ/mole at 298 K. Explain why those values are different.

Q3.25

What is ΔH if of 3.00 moles of O₂(g) are cooled from 175^ºC to 35.0^ºC and \[\bar{C_{p}} = (7.50 \times 10^{-3}T - 2.30 \times 10^{-6}T^{2} J mol^{-1} K^{-1}\]

S3.25

\[dH = n\bar{C_{p}}dT\]

\[\Delta H = (3 mol) \int_{448K}^{308K}(7.50 \times 10^{-3}T - 2.30 \times 10^{-6}T^{2}) J mol^{-1} K^{-1}dT\]

\[\Delta H = (3 mol) (\dfrac{7.50 \times 10^{-3}}{2}T^{2} - \dfrac{2.30 \times 10^{-6}}{3}T^{3} J mol^{-1} K^{-1} | _{448K}^{308K})\]

\[\Delta H = (3 mol) [(3.75 \times 10^{-3}(308K)^{2}-7.67 \times 10^{-7}(308K)^{3})-(3.75 \times 10^{-3}(448K)^{2}-7.67 \times 10^{-7}(448K)^{3})]J mol^{-1} K^{-1}\]

\[\Delta H = (3 mol) [(333.3)-(683.7)]J mol^{-1}\]

\[\Delta H = -1050 J \]

Q3.25

For a constant-pressure process, the heat capacity per mole is given by the expression:

C_p per mole = (16.0 + 4.35 x 10^-3 T + 1.15 T²) J K^-1 mol^-1

Find the molar heat capacity of oxygen gas from 38°C to 115^oC

S3.25

\[\begin{align} \Delta H &=\int_{38}^{115}(16+4.35 \times 10^{-3}T+1.15T^{2})dT \\ &= (16*115+(4.35 \times 10^{-3})/2 * 115^2 + 1.15/3 *115^3) - (16*38 +(4.35 \times 10^{-3})/2 *38^2 +1.15/3 * 38^3) \\ &= 5.63 J/mol \end{align}\]

Q3.26

What is the heat capacity ratio (\(γ\)) if of an ideal gas if its \(C_V = 42\, J\, K^{-1} mol^{-1}\)?

S3.26

since \(\overline{C_{P}} = \overline{C_{V}} + R\)

\[\begin{align} \gamma = \dfrac{\overline{C_{P}}}{\overline{C_{V}}} &= \dfrac{\overline{C_{V}}+R}{\overline{C_{V}}} \\ \gamma &= \dfrac{(42+8.314) J K^{-1} mol^{-1}}{42J K^{-1} mol^{-1}} \\ \gamma &= 1.2 \end{align}\]

Q3.29

Explain (in terms of thermo chemistry) why Emperor Penguins huddle together in the Antarctic.

Q3.30a

Through laboratory experiment, a group of students found out that molar mass of a solid element can be calculated in term of the specific heat capacity :

Molar mass x the specific heat of metals= 25 (Eq.1)

They were also obtaining the values of the three metals, Aluminum (0.900 J/g ^oC), Zinc (0.381 J/g ^oC), and Arsenic (0.329 J/g ^oC).

Determine which metal violate the above equation (Eq.1)

S3.30a

Aluminum (Al) can not be applied in this equation because the specific heat capacity of Al is approximately equal 1.0 J g^-1 (^oC^-1)

Q3.30b

What is the molar heat capacity of lead given its specific heat is 0.128J/(gºC) at 25ºC?

S3.30b

The first thing we do is find the molar mass of lead which is 207.2 g/mol.

We multiply our molar mass by the specific heat to get the molar heat capacity.

Q3.31

What is the total work done on 2.00 moles of an ideal monatomic gas at 3.00 atm and 4.00 L when it adiabatically expands to 7.00 L?

S3.31

The equation for work is

\[w = n \bar{C_{V}} (T_{2} - T_{1})\]

For a monatomic gas,

\[\bar{C_{V}} = \dfrac{3}{2}R \ and \ \bar{C_{P}} = \dfrac{5}{2}R\]

\[\gamma = \dfrac{\bar{C_{P}}}{\bar{C_{V}}} = 1.67\]

Solve for T₁:

\[PV=nRT\]

\[T_{1}=\dfrac{PV}{nR}=\dfrac{(3 atm)(4L)}{(2 moles)(0.08206 \dfrac{L \ atm}{mol \ K})}\]

\[T_{1} = 73.12 K\]

Solve for T₂:

\[P_{1}V_{1}^{\gamma} = P_{2}V_{2}^{\gamma}\]

\[P_{2}=\dfrac{(3atm)(4L)^{1.67}}{(7L)^{1.67}}=1.178atm\]

\[T_{2}=\dfrac{PV}{nR}=\dfrac{(1.178 atm)(7L)}{(2 moles)(0.08206 \dfrac{L \ atm}{mol \ K})}\]

\[T_{2}=50.24K\]

Solve for work:

\[w = n \bar{C_{V}} (T_{2} - T_{1})\]

\[w = (2 mol)(\dfrac{3}{2})(8.314 \dfrac{J}{mol \ K})(50.24K - 73.12 K)\]

\[w = -571 J\]

Q3.31

You notice your system changes volume from 10 L to 30 L with a constant pressure at 770 torr. Then, there is a decrease in pressure to 740 torr with the volume staying constant at 30 L. Calculate the total amount of work done.

S3.31

We split up the solution into two parts.

Work done during the volume change and the work done during the pressure change.

First part:

Second part:

Convert pressure to atm:

=107.4 J

Then add up the two works

w_tot= -2046.3+107.4=-1938.9 J

Q3.33

Calculate the values of q, w, ΔU, and ΔH for the reversible adiabatic expansion of 1 mole of a diatomic ideal gas from 10.00 m³ to 35.0 m³ with an initial temperature of 298 K.

Q3.33

Calculate the values of q, w, ΔU, and ΔH for the reversible adiabatic expansion of 1 mole of a diatomic ideal gas from 10.00 m³ to 40.0 m³ with an initial temperature of 298K.

Q3.34

A quantity of 0.27 mole of argon is confined in a container at 3.0 atm and 298 K and then allowed to expand adiabatically under two different conditions: (a) reversibly to 0.80 atm and (b) against a constant pressure of 0.80 atm. Calculate the final temperature in each case.

Q3.34

In an adiabatic process 0.5 moles of He_2­ in a container are allowed to expand against a constant pressure of 1.00 atm and 298 K. The final temperature after the gas has expanded is 205 K. Calculate the initial pressure inside the container.

S3.34

In an adiabatic process

\(C_{V}=(T_{2}-T_{1})=-P_{ex}(V_{2}-V_{1})\)

we get

\(\dfrac{3}{2}(T_{2}-T_{1})=-P_{ex}\left ( \dfrac{T_{2}}{P_{2}}-\dfrac{T_{1}}{P_{1}} \right )\)

we rearrange and get

 \(\dfrac{3}{2}(T_{2}-T_{1})=\dfrac{P_{ex}T_{1}}{P_{1}}-T_2\)

we solve for

\(P_{1}\) and get \(P_{1}=\dfrac{P_{2}}{\dfrac{T_{2}}{T_{1}}(\dfrac{5}{2})-\dfrac{3}{2}}\)

\(P_{1}=\dfrac{1.00atm}{\dfrac{205K}{298K}(\dfrac{5}{2})-\dfrac{3}{2}}\)

\(P_{1}=4.5 atm\)

Q3.34

A quantity of 0.27 mole of argon is confined in a container at 3.0 atm and 298 K and then allowed to expand adiabatically under two different conditions:

1. reversibly to 0.80 atm and
2. against a constant pressure of 0.80 atm.

Calculate the final temperature in each case.

Q3.35a

Two moles of ideal diatomic gas \(H_2\) expand from 2.00 atm to 1.30 atm while being cooled from 550 K to 250 K. Compute the Change of Enthalpy (∆H) and Change of Internal Energy (∆U) for 2 different processes: a. reversible and b. irreversible. Explain and calculate the difference a and b?

Q3.35b

0.5 mole of Helium at 298 K are allowed to expand reversibly from 5 atm to 1 atm. Find q, w and ΔU if

1. the process is adiabatic and
2. if the process is isothermal.

Q3.36a

808 kJ/mol of heat is released by burning x (gram) amount of Iron in a constant volume bomb calorimeter. The calorimeter containing 100 g water inside has a heat capacity of 2100 JoC^-1. Evaluate the amount of Iron needed to increase the water by 5.20C?

Q3.36b

In your constant-volume bomb calorimeter you have a 0.3677 g sample of Potassium. The water surrounding the sample increase from 18.08 ºC to 20.667 ºC. The calorimeter has a heat capacity of 1515 J/(gºC). What is the change in internal energy?

S3.36b

Since the bomb calorimeter has a constant volume \(\Delta V\), there is no (PV) work so the first law of thermodynamics

\[\Delta U =q +w\]

can be simplified to

\[ \Delta U = q\]

Then the relationship between heat and temperature change

\[q = c_v \Delta T\]

can be changed

\[\Delta U = m \,c_v\, \Delta T\]

which for this case is

\[\Delta U= ( 0.3677\;g ) (1,515\; J/(gºC)) (20.667 \;ºC -18.08 \; ºC)\]

\[\Delta U =1411.1\]

Q3.37

The enthalpy of combustion for benzoic acid (\(C_6H_5COOH\)) is commonly used as the standard \(\Delta H_{combustion} = -3226.7\,kJ\,mol^{-1}\), for calibrating bomb calorimeters at a constant-volume process.

1. When 1.567 g of benzoic acid burned in a calorimeter the temperature increased by \(3.678^{o}C\). Calculate the heat capacity of the calorimeter.
2. For a different experiment 0.6792g of ethanol was burned in the calorimeter which rose from 16.42\(^{o}\)C to 26.58\(^{o}\)C. Calculate the enthalpy of combustion for ethanol, the value of \(\Delta rU\) for the combustion, and the molar enthalpy of formation.

S3.37

(a)

\[q_{calorimeter}=-q_{benzoic\,acid} \]

\[q_{calorimeter}(3.678^{o}C)=-(\dfrac{1.567g}{122.1g\,mol{-1}})(-3226.7kj\,mol^{-1})\]

\[c_{calorimeter}=\dfrac{41.41kj}{3.678^{o}C}=11.26kj^{o}C^{-1}\]

(b) (Hint: Calorimeter absorbs heat transfered from the combustion of maltose)

\[q_{calorimeter}=-q{maltose}\]

Step 1: Calculate \(\Delta rU\)

\[(11.26kj\,^{o}C^{-1})(26.58^{o}C-16.42^{o}C)=-(\dfrac{.6792g}{46.06844gmol^{-1}})(\Delta rU^{o})\]

\[\Delta\,rU^{o}=-\dfrac{114.4016kj}{.014743282mol}=-7.759\times10^{3} jk\, mol^{-1}\]

Step 2: Calculation of enthalpy of combustion

\[C_2H5OH_{(s)}+3O_{2\,(g)}\rightarrow2CO_{2(g)}+3H_2O_{(l)}\]

\(\Delta n=-1\)

Therefore,

\[\Delta rH^{o}=\Delta rU^{o}+RT\Delta n=(-7.759\times10^{3}kj\,mol^-1)+(8.3146\times10^{-3}kj\,mol^{-1}K^{-1})(298.15K)(-1)=-7.761\times10^{3}kj\,mol^{-1}\]

Step 3: Calculate the molar enthalpy of formation.

\[\Delta rH=2\Delta _f\bar{H}^{o}[CO_{2(g)}]+3\Delta _f\bar{H}^{o}[H_2O_{(l)}]-\Delta _f\bar{H}^{o}[C_2H_5OH_{(s)}]-3\Delta _f\bar{H}^{o}[O_{2(g)}]\]

\[=2(-393.5kj\,mol^{-1})+3(-285.8kj\,mol^{-1})-3(0kj\,mol^{-1})-(-7.761\times10^{3}kj\,mol^{-1})\]

\[=6.116\times10^{3}kj\,mol^{-1}\]

Q3.38a

A quantity of 2.50 x 10² mL of 0.468 M HBr is mixed with 2.50 x 10² mL of 0.425 M KOH in a constant-pressure calorimeter that has a heat capacity of 437 J °C^-1. The initial temperature if the HBr and KOH solutions is the same at 21.35°C. For the process

\[H^+(aq) + OH^-(aq) \rightleftharpoons H_2O(l)\]

the heat of neutralization is -56.2 kJ mol^-1. What is the final temperature of the mixed solution?

Q3.38b

In a constant-pressure calorimeter with a heat capacity of 395\(J\,^{o}C^{-1}\), you mix \(1.5\times10^{3}\,mL\) of HBr at 0.788M and \(1.5\times10^{3}mL\) \(Ca(OH)_2\) at .394M. For this process to occur the heat of neutralization is \(-56.2kj\,mol^{-1}\). The initial temperature of both solutions is \(23.08^{o}C\).

\[H^+_{(aq)}+OH^-_{(aq)}\rightarrow H_2O_{(l)}\]

Find the final temperature of the mixed solution.

S3.38b

Step 1: (Hint: Determine the number of moles of the reactants)

\[n_{H^{+}}=(1.5L)(0.788\,mol\,L^{-1})=1.182\,mol\]

\[n_{OH^{-}}=2(1.5L)(0.394\,mol\,L^{-1})=1.182\,mol\]

Step 2: (Hint: Calculate the the thermal energy released by the reaction)

\[q_P=(-52.2\,kJ\,mol^{-1})(1.182\,mol)=-66.42\, kJ\]

Step 3: (Hint: Assume the the density of the solutions are the same as water and specific heat is same as water too.)

\[s_{solution}=4.184\,J\, g^{-1}^{o}C^{-1}\]

\[m_{solution}=m_{HBr}+m_{Ca(OH)_2}\]

\[=(1.5 \times 10^{3}mL)(1.00gmL^{-1})+(1.5 \times 10^{3}mL)(1.00gmL^{-1})=3.00 \times 10^3g\]

Step 4:

\[66.4284\, kJ=395J^{o}C^{-1}+(3.00 \times 10^{3}g)(4.184\, J\, g^{-1}\,^{o}C^{-1})(\dfrac{1kJ}{1000\,J})\Delta T\]

\[66.4284=(12.947^{o}C^{-1})\Delta T\]

\[\Delta T=5.13^{o}C\]

Step 5:

\[\Delta T=T_f-T_i\]

\[T_f=28.21^{o}C\]

Q3.38

A quantity of \(2.50 \times 10^2\; mL\) of \(0.468;\; M \;HBr\) is mixed with \(2.50 \times 10^2\; mL\) of \(0.425\; M\; KOH\) in a constant-pressure calorimeter that has a heat capacity of 437 J °C^-1. The initial temperatures of the \(HBr\) and \(KOH\) solutions are the same at 21.35 °C. The heat of neutralization for the below reaction is \(-56.2\; kJ/mol^\)

\[H^+_{(aq)} + OH^-_{(aq)} \rightarrow H_2O_{(l)}\]

What is the final temperature of the mixed solution?

Q3.39

1.52 g of toluene \((C_7H_8)\) is combusted in a constant volume bomb calorimeter at 25°C. Calculate the \(\Delta _r\bar{U}\) and \(\Delta _r\bar{H}\) for this reaction given that 39.183 kJ of heat was released.

S3.39

First we need to construct the balanced reaction that occurs

\[C_7H_8(l)+9O_2(g)\rightarrow7CO_2(g)+4H_2O(l)\]

\(\Delta _r\bar{U}=q_r=-q_{cal}=\dfrac{-39.183kJ}{\dfrac{1.52g}{92.14(g/mol)}}=-2375\; kJ/mol\)

\(\begin{align*}
\Delta _r\bar{H}&=\Delta _r\bar{U}+\Delta (PV)=\Delta _r\bar{U}+\Delta n(RT)\\&=-2375 \; kJ/mol + (-2)(8.314 \times 10^{-3}\; kJ/K*mol)(298.15\; K)=-2380 \; kJ/mol \end{align*} \)

Q3.39

The of ΔU a of the combustion of naphthalene (C₁₀H₈) are -480 kj mol^-1. The heat evolved from the combustion in a constant-volume calorimeter is 7.5 KJ. Calculate the mass of naphthalene in grams in the calorimeter.

Q3.40

For the reaction

\[C_2H_5OH_{(l)} + O_{2 (g)} \rightarrow CO_{2 (g)} + H_2O_{(l)}\]

1. Balance the reaction
2. Calculate the \(∆_rH\) of reaction using the \(∆_fH\) data

Q3.40B

Consider the following reaction:

\[\begin{align*}C_2H_6(g)+\dfrac{7}{2}O_2(g)\rightarrow &2CO_2(g)+3H_2O(l)\\
&\Delta_rH^\circ=-1560kJ/mol\end{align*}\]

What is the value of \(\Delta_rH^\circ\) if

1. the equation is multiplied throughout by 4;
2. the direction of the reaction is reversed;
3. \(C_2H_6\) was a liquid instead of gas?

S3.40B

1. \(\Delta_rH^\circ=4(-1560kJ/mol)=-6240kJ/mol\);
2. \(\Delta_rH^\circ=1560kJ/mol\);
3. Ethane exist as a liquid at temperatures of below 184.6 K. If we used ethane liquid instead of ethane gas, then according to \[\Delta H=\Delta U+\Delta n(RT)\] the number of moles would change and the temperature of the reaction would also change.

Q3.41a

On what basis is the 0 value for standard enthalpy of formation assigned to a substance at a specific temperature? Base on that, identify which substances have Δ_fH° = 0 and which do not at 1 atm and 25°C (give explanation for those that do not).

H₂(g), O₃(g), Al(s), Br₂(g), NaCl(s), Cl2(g)

Hint: Look at standard enthalpy of formation

S3.41a

0 value for standard enthalpy of formation is assigned to elemental substances that are in their natural/standard physical state at that specific condition of temperature and pressure.

1. H₂(g), Al(s), Cl₂(g) are substances with Δ_fH° = 0 kJ/mol
2. O₃(g) is an elemental substance but does not occur naturally at 25°C, O₂(g) is.
3. Br₂(g) is also not the standard state of bromine. At STP, the physical state of bromine is liquid
4. NaCl does not have a 0 value because it is not an elemental substance

Q3.41b

Which of the following substances has a standard enthalpy of formation, at 298 K, of 0 K?

O₂(g), Br₂(g), Hg(s), CH₄(g)

Q3.41c

Why is the standard enthalpy of formation of O₂ zero at a temperature of 298 K?

S3.41c

The standard enthalpy of formation of O₂ is zero at 298 K since O₂ is the most stable allotropic form of oxygen at that particular temperature.

Q3.42a

a) The ionization of a weak acetic acid is written as:

\[ CH_{3}COOH(aq) \rightleftharpoons CH_{3}COO^{-} + H^+ \]

Suppose the change of reaction enthalpy for this reaction is +1.0 kJ/mol and the Δ_fH° of CH₃COO^- is -486.01 kJ/mol. What would be the molar enthalpy of formation of aqueous acetic acid?

b) The acetic acid is reacted with a strong base NaOH. Calculate the enthalpy of neutralization for this reaction of weak acid strong base.

Δ_fH°[OH^-(aq)] = -229.6 kJ/mol and Δ_fH°[H₂O(l)] = -285.8 kJ/mol

Hint: Look at enthalpy of neutralization

S3.42a

a) \[\Delta _r \bar{H}^{\circ} = \sum{[\Delta_{f} \bar{H}^{\circ}}]reactants - \sum{[\Delta_{f} \bar{H}^{\circ}}]products\]

\[\Delta _r \bar{H}^{\circ} = \Delta_{f} \bar{H}^{\circ}[CH_{3}COO^-] + \Delta_{f} \bar{H}^{\circ}[H^+] - \Delta_{f} \bar{H}^{\circ}[CH_{3}COOH]\]

\[+1.0 \dfrac{kJ}{mol} = -486.01 \dfrac{kJ}{mol} + 0 \dfrac{kJ}{mol} - \Delta _f \bar{H}^{\circ}[CH_{3}COOH]\]

\[ {\color{red} \Delta _f \bar{H}^{\circ}[CH_{3}COOH] = -487.01 \dfrac{kJ}{mol}}\]

b) Note that acetic acid is a weak acid, therefore only dissociates partially or does not dissociate at all. Therefore the complete ionic reaction of reaction is:

\[CH_{3}COOH(aq) + Na^+ (aq) + OH^- (aq) = CH_3COO^- (aq) + Na^+ (aq) + H^2O(l)\]

Since Na⁺ cancels out, the net equation is

\[CH_{3}COOH(aq) + OH^- (aq) = CH_3COO^- (aq) + H^2O(l)\]

\[\Delta _r \bar{H}^{\circ} = \Delta_{f} \bar{H}^{\circ}[CH_{3}COO^-] + \Delta_{f} \bar{H}^{\circ}[H_2O] - \Delta_{f} \bar{H}^{\circ}[CH_{3}COOH] - \Delta_{f} \bar{H}^{\circ}[OH^-] \]

\[\Delta _r \bar{H}^{\circ} = (-486.01 -285.5 + 486.01+229.6) \dfrac{kJ}{mol}\]

\[ {\color{red}\Delta _r \bar{H}^{\circ} = -55.9 \dfrac{kJ}{mol}}\]

Q3.42b

Calculate the enthalpy of formation for Br^- ions in the following reactions:

1. \(HBr(g)\rightarrow Cl^-(aq) + Br^+(aq)\)
2.  \( \Delta _rH^\circ =-105.7\dfrac{kJ}{mol}\)

S3.42b

\[\Delta _rH^\circ =\Delta _f\overline{H}^\circ (H^+)+\Delta _f\overline{H}^\circ (Br^-)-\Delta _f\overline{H}^\circ (HBr)\]

\[ \Delta _f\overline{H}^\circ (Br^-)=\Delta _rH^\circ -\Delta _f\overline{H}^\circ (H^+)+\Delta _f\overline{H}^\circ (HBr)\]

\[\Delta _f\overline{H}^\circ (Br^-)=36.4\dfrac{kJ}{mol} -0+(-.105.7\dfrac{kJ}{mol})\]

\[\Delta _f\overline{H}^\circ (Br^-)=69.3\dfrac{kJ}{mol}\]

Q3.42c

When determining standard enthalpies of formation of ions in aqueous solutions, set the value of \(H^+\) ion to 0 for \(\Delta _{f}\bar{H}^o[H^{+}_{(aq)}]=0.\)

1. For the following reaction \(HBr_{(g)}\rightarrow H^+_{(aq)}+Br^-_{(aq)} \), \(\Delta rH^{o}=-98.4kj\,mol^{-1}\). Calculate the value of \(\Delta _f\bar{H}^o\) for the Br ions.
2. The standard enthalpy of neutralization between HBr and NaOH solutions is \(-53.4kj\,mol^{-1})\). At \(25^{o}C\), calculate the standard enthalpy of formation of the hydroxide ion.

S3.42c

(a)

$$\Delta rH^{o}=-98.4kj\,mol^{-1}=\Delta _f\bar{H}^{o}[H^+_{(aq)}]+\Delta _f\bar{H}^{o}[Br^-_{(aq)}]-\Delta _f\bar{H}^{o}[HBr_{(g)}]\]

$$\Delta _f\bar{H}^{o}[Br^-_{(aq)}]=-98.4kj\,mol^{-1}-\Delta _f\bar{H}^{o}[H^+_{(aq)}]+\Delta _f\bar{H}^{o}[HBr_{(g)}]\]

$$=-98.4kj\,mol^{-1}-0kj\,mol^{-1}+(-36.29kj\,mol^{-1})\]

$$=-134.69kj\,mol^{-1}\]

(b) The neutralization for 1 mole of \(H_2O\) is \(\Delta rH^{o}=-53.4kj\,mol^{-1}\)

$$\Delta rH^{o}=\Delta_f\bar{H}^{o}[H_2O_{(l)}]-\Delta_f\bar{H}^{o}[H^+_{(aq)}]-\Delta_f\bar{H}^{o}[OH^-_{(aq)}]\]

$$\Delta_f\bar{H}^{o}[OH^-_{(aq)}]=\Delta_f\bar{H}^{o}[H_2O_{(l)}]-\Delta_f\bar{H}^{o}[H^+_{(aq)}]+53.4kj\,mol^{-1}\]

$$=(-285.8kj\,mol^{-1})-0kj\,mol^{-1}+53.4kj\,mol^{-1}\]

$$=-232.4kj\,mol^{-1}\]

Q3.42d

For the following chemical reaction, calculate the Δ_rH^º.

\[ \begin{align} H_{3}PO_{4} (aq) & \rightarrow H_{2}PO_{4}^{2-}(aq) + H^{+} (aq) \\ \triangle _{f}H^{\circ}_{H_{3}PO_{4}(aq)} & = -1277 \ \ kJ \ mol^{-1} \\ \triangle _{f}H^{\circ}_{H^{+}(aq)} & = \ \ 0 \ \ kJ \ mol^{-1} \\ \triangle _{f}H^{\circ}_{H_{2}PO_{4}^{2-}(aq)} & = -1302.5 \ \ kJ \ mol^{-1} \end{align}\]

S3.42d

Use the following equation:

\[ \Delta H_{reaction}^o = \sum {\Delta H_{f}^o(products)} - \sum {\Delta H_{f}^o(Reactants)}\]

Solve

\[ \begin{align} \Delta H_{reaction}^o & = \Delta H_{f}^o(H_2PO_4^{2-})+\Delta H_{f}^o(H^{+}) - \Delta H_{f}^o(H_3PO_4)\\ & = -1302.5 \ kJ \ mol^{-1} - (-1277 \ kJ \ mol^{-1}) \\ & \underline {= -25.5 \ kJ \ mol^{-1}} \end{align}\]

Click here for more information about standard enthalpies of reaction.

Q3.42e

The reaction for the dissociation of hydrobromic acid in water is as follows:

\[HBr_{(g)}\rightleftharpoons H^{+}_{(aq)}+Br_{(aq)}^{-}\, \, \, \, \, \, \, \, \, \, \, \, \Delta _{r}H^{\circ}=-85.2\frac{KJ}{mol}\]

\[\Delta _{f}H^{\circ}(HBr)=-36.4\frac{KJ}{mol}\]

a.) Given the enthalpy of formation for HBr, what is the enthalpy of formation for the Bromine ion? Assume that the enthalpy of formation for the Hydrogen ion is 0.

b.) What is the enthalpy of reaction for the neutralization of HBr with KOH? Assume that the potassium and bromine ions remain in solution following the neutralization.

\[\Delta _{f}H^{\circ}(OH_{(aq)}^{-})=-36.4\frac{KJ}{mol} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \Delta _{f}H^{\circ}(H_{2}O_{(l)})=-285.8\frac{KJ}{mol} \]

S3.42e

a.) For any reaction,

\[\Delta _{r}H^{\circ}=\sum \nu \Delta _{f}\bar{H}^{\circ}(products)-\sum \nu \Delta _{f}\bar{H}^{\circ}(reactants)\]

For this reaction,

\[\Delta _{r}H^{\circ}= \Delta _{f}\bar{H}^{\circ}(Br^{-}_{(aq)})+\Delta _{f}\bar{H}^{\circ}(H_{(aq)}^{+})-\Delta _{f}\bar{H}^{\circ}(HBr_{(aq)})\]

\[\Delta _{f}\bar{H}^{\circ}(Br^{-}_{(aq)})=\Delta _{r}H^{\circ}+\Delta _{f}\bar{H}^{\circ}(HBr_{(aq)})\]

\[=\left (-85.2\frac{KJ}{mol} \right )+\left (-36.4 \frac{KJ}{mol} \right )=-121.6\frac{KJ}{mol}\]

b.) For any neutraliztion reaction in solution,

\[OH_{(aq)}^{-}+H_{(aq)}^{+}\rightleftharpoons H_{2}O_{(l)}\]

\[\Delta _{r}H^{\circ}= \Delta _{f}\bar{H}^{\circ}(H_{2}O_{(l)})-\Delta _{f}\bar{H}^{\circ}(OH_{(aq)}^{-})\]

\[=-285.8\frac{KJ}{mol}-\left ( -36.4 \frac{KJ}{mol}\right )=-249.4\frac{KJ}{mol}\]

Q3.43a

How much heat is given off when one explodes 24.65 grams of nitroglycerin? The equation for the combustion of nitroglycerin is given below:

\[ \begin{align} & 4 C_3H_5N_3O_9(l) \rightarrow 12 CO2(g) + 10 H_2O(g) + 6 N_2(g) + O_2(g) \\ & \triangle _{r}H^{\circ}_{C_3H_5N_3O_9(l)}= -1.529 \ MJ \ mol^{-1} \end{align}\]

S3.43a

The molar mass of nitroglycerin is 227.0865 g/mol.

To solve this question simply multiple the enthalpy of reaction by the amount moles of nitroglycerin.

\[ \begin{align} 24.65 \ g \div 227.0865 \ g \ mol^{-1} \ &= 0.109 \ moles \ of \ nitroglycerin \\ 1.529 \ MJ \ mol^{-1} \cdot 0.109 \ mol &= \underline{ 0.166 MJ \ of \ heat } \end{align}\]

Q3.43b

What is the enthalpy change from the formation of 5 grams of H₂CO₃ via CO_2(g) + H₂O_(g) àH­­₂CO_3(g) H₂CO_{3 (g)} via CO_{2 (g)} + H₂O _(g) → H₂CO_{3 (g)}? The change in enthalpy associated with this reaction is +360.19 kJ/mol.

S3.43b

The enthalpy change from this reaction is given by the molar enthalpy change times the number of moles of product formed. Thus:

m_co2 = 44.01 g mol_­^-1 ;

n_co2 = 5g /44.01 g mol^-1 = 0.1136 mol

ΔH =0.1136 mol * 360.19 kJ/mol = 40.9kJ

Q3.43c

The following reaction was carried out at standard temperature and pressure:

\[2C_{(graphite)}+3H_{2(g)}\rightarrow C_{2}H_{6(g)}\, \, \, \, \, \, \, \, \, \, \Delta _{r}H^{\circ}=-84.7\frac{KJ}{mol}\]

If -148.16 KJ of heat was released during this reaction, how many grams of Ethane were formed?

S3.43c

For any reaction:

\[q=n\Delta _{f}H^{\circ}=\frac{m}{\mathfrak{M}}\Delta _{f}H^{\circ}\]

This can be rearranged as

\[m=\frac{q\mathfrak{M}}{\Delta _{f}H^{\circ}}\]

The molar mass of ethane is

\[\mathfrak{M}=2(12.01 \frac{g}{mol})+6(1.008\frac{g}{mol})=30.07 \frac{g}{mol}\]

The mass of ethane produced, then, is

\[m=\frac{q\mathfrak{M}}{\Delta _{f}H^{\circ}}=\frac{(-148.16 KJ)(30.07\frac{g}{mol})}{-84.7\frac{KJ}{mol}}=52.6g\]

Q3.44a

When 2.3 g of calcium carbonate is decomposed under constant pressure, 178.3 kJ of heat were released. What is the \(\Delta_rH^\circ \) for this reaction?

\[CaCO_3(s)\rightarrow CaO(s)+CO_2(g)\]

S3.44a

\[\Delta _rH^\circ = q_p=\dfrac{178.3kJ}{\dfrac{2.3g}{100.09g/mol}}=7759.15kJ/mol\]

Q3.44b

In a high school chemistry experiment, 10 grams of methane were combusted in the presence of excess oxygen under standard conditions. A calorimeter measured that 554.9 kJ of heat were released by the reaction to the surroundings. Assuming the calorimeter’s measurement accounts for all heat changes associated with the reaction, write the reaction for the combustion of methane and calculate the change in enthalpy associated with it.

Q3.46

The isomerization process from 1-butene to 2-butene has a reaction enthalpy of -7.1 kJ/mol.

=

1-butene 2-butene

If the hydrogenation of 1 butene has a reaction enthalpy of -126.8 kJ/mol. How much energy would the hydrogenation of 2-butene takes? Keep in mind that both processes yield the same product.

Hint: Look at example problems of change of standard reaction enthalpy

S3.46

1-butene + 2H₂ → butane Δ_fH° = -126.8 kJ/mol

1-butene → 2-butene Δ_fH° = -7.1 kJ/mol

Reverse the 2nd reaction and combine the two reactions

1-butene + 2H₂ → butane Δ_fH° = -126.8 kJ/mol

2-butene → 1-butene Δ_fH° = +7.1 kJ/mol

Δ_rH° = -126.8 kJ/mol +7.1 kJ/mol

Δ_rH° = -119.7 kJ/mol

Q3.47a

From the reaction below, calculate the enthalpy of formation of methane gas.

\[ \begin{align} & CH_4(g) + 2 O_2(g) \rightarrow CO_2(g) + 2 H_2O(l) \\ & \triangle _{r}H^{\circ} = -891 kJ \ mol^{-1} \\ & \triangle _{f}H^{\circ}_{CO_2(g)} = -393.5 kJ \ mol^{-1} \\ & \triangle _{f}H^{\circ}_{H_2O (l)} = -285.8 kJ \ mol^{-1} \end{align}\]

S3.47a

Use the following equation:

\[ \Delta H_{reaction}^o = \sum {\Delta H_{f}^o(products)} - \sum {\Delta H_{f}^o(Reactants)}\]

Plug in appropriate values and solve. Change in enthalpy of oxygen is 0 because it is the reference form of a pure element.

\[ \Delta H_{r}^o = \Delta H_{f}^o(CO_2) + (2 \cdot \Delta H_{f}^o(H_2O)) - (2 \cdot \Delta H_{f}^o(O_2)) - \Delta H_{f}^o(CH_4)\]

\[ \begin{align} -891 \ kJ \ mol^{-1}&=(-393.5 \ kJ \ mol^{-1}) + (-285.8 \ kJ \ mol^{-1}) - (\Delta H_{f}^o(CH_4)) \\ \Delta H_{f}^o(CH_4)&= \underline{ 211.7\ kJ \ mol^{-1} } \end{align}\]

Click here for more information on standard enthalpies.

Q3.47b

For the following combustion reaction:

\[C_{3}H_{7}OH_{(l)}+3O_{2(g)}\rightarrow 4H_{2}O_{(l)}+3CO_{2(g)}\, \, \, \, \, \, \, \, \, \, \,\Delta _{r}H^{\circ}=-2005.8\frac{KJ}{mol}\]

Calculate the enthalpy of formation for 2-propanol, given the following enthalpies of formation

\[\Delta _{f}\bar{H}^{\circ}(H_{2}O)=-285.8 \frac{KJ}{mol}\, \, \, \, \, \, \, \, \, \, \, \, \, \, \Delta _{f}\bar{H}^{\circ}(CO_{2})=-393.5 \frac{KJ}{mol}\]

S3.47b

In general:

\[\Delta _{r}H^{\circ}=\sum \nu \Delta _{f}\bar{H}^{\circ}(products)-\sum \nu \Delta _{f}\bar{H}^{\circ}(reactants)\]

In general,

\[\Delta _{r}H^{\circ}=3 \Delta _{f}\bar{H}^{\circ}(CO_{2})+4\Delta _{f}\bar{H}^{\circ}(H_{2}O)-\Delta _{f}\bar{H}^{\circ}(C_{3}H_{7}OH)\]

\[\Delta _{f}\bar{H}^{\circ}(C_{3}H_{7}OH)=3 \Delta _{f}\bar{H}^{\circ}(CO_{2})+4\Delta _{f}\bar{H}^{\circ}(H_{2}O)-\Delta _{r}H^{\circ}\]

\[=3\left (-393.5\frac{KJ}{mol} \right )+4\left (-285.8\frac{KJ}{mol} \right )-\left (-2005.8\frac{KJ}{mol} \right )=-317.9 \frac{KJ}{mol}\]

Q3.48

Diatomic fluorine gas has a Cp of 31.3 J/K*mol. What is its molar enthalpy of formation on the surface of the planet Venus (at standard pressure), where temperature is commonly 465 C?

S3.48

At constant pressure, the change in enthalpy with respect to temperature is given by Cp. By determining the change in temperature and multiplying it by Cp we can find the change in enthalpy.

ΔT = 465 C - 25 C = 440K

ΔH = 31.3 J/K*mol * 440K = 13.772 kJ/mol

Q3.50

The combustion of graphite is

C(gr) + O₂(g) → CO₂(g)

Calculate the change in the enthalpy of combustion from 298 K to 398 K. The molar C_p values are (in J K^-1 mol^-1): C(gr):8.52, O₂(g):29.4, and CO₂(g):37.1

Q3.53

What values are needed to calculate the change in standard enthalpy of a reaction?

Q3.54

Consider the following reactions:

C(graphite) + O_{2 (g)} → CO (s) ∆_rH = -110.5 kJ/mole

CO₂ (g) → Co (s) + O_{2 (g)} ∆_rH = 283.0 kJ/mole

Find the enthalpy of formation of carbon dioxide (CO₂₎

S3.54

The \(\Delta H\) of the reaction is the sum of \(\Delta H_1\) and \(\Delta H_2\)

\[2C + O_2 \rightarrow 2CO \,\,, \Delta H_1 = -110.5 kJ/mol

\[2CO + O2 \rightarrow 2CO_2 \Delta H_2 = -283 kJ/mol

thus the \(\Delta H\) of reaction is (-110.5)+(-283.0) = -393.5 kJ/mol

Q3.55

What is Δ_rH^º of the following reaction? Δ_fH^º for O(g) is 249.4 kJ mol^-1 and Δ_fH^º for O₃(g) is 142.7 kJ mol^-1

\[2O_{2(g)} \rightarrow O_{(g)} + O_{3(g) }\]

S3.55

\[\Delta H^{\circ}_{rxn} = \sum \Delta H^{\circ}_{prod} - \sum \Delta H^{\circ}_{reactants}\]

\[\Delta H^{\circ}_{rxn} = [\Delta H^{\circ}(O(g)) +\Delta H^{\circ}(O_{3}(g))]-2\Delta H^{\circ}(O_{2}(g))\]

\[\Delta H^{\circ}_{rxn} = (249.4 + 142.7) \dfrac{kJ}{mol} \]

\[\Delta H^{\circ}_{rxn} = 392.1 \dfrac{kJ}{mol} \]

Q3.60

Methane combusts, what is the enthalpy of combustion for this reaction?

Substance	Standard Molar Enthalpies of Formation at 25ºC
CH4(g)	-74.85 kj/mol
CO2(g)	-393.5 kj/mol
H2O(g)	-241.8 kj/mol
H2O(l)	-285.8 kj/mol

S3.60

Write the balanced formula for this reaction to identify the coefficients

\[CH_{4(g)} +2 O_{2(g)} \rightarrow 2H_2O_{(l)} + CO_{2(g)}\]

\[\Delta H= \sum H_{products} - sum H_{reactants}\]

\[= 2x H(H_2O) + H(CO_2) - H(CH_4)\]

We do not include \(O_2\) because it is a standard state

\[=[(2 x -285.8 + -393.5) - (-74.85)] kJ/mol\]

\[=-890.25\; kJ/mol\]

Q3.62

Predict whether the values of q, w, ΔU, and ΔH are positive, zero, or negative for each of the following processes: (a) freezing of ice at 1 atm and 273 K, (b) melting of solid butanol at 1 atm and the normal melting point, (c) reversible isothermal compression of an ideal gas, and (d) reversible adiabatic compression of an ideal gas.

Q3.62

Predict whether the values of q, w, ΔU, and ΔH are positive, zero, or negative for each of the following processes: (a) freezing of ice at 1 atm and 273 K, (b) melting of solid butanol at 1 atm and the normal melting point, (c) reversible isothermal compression of an ideal gas, and (d) reversible adiabatic compression of an ideal gas.

Q3.63

The first law of thermodynamics states that energy is conserved. It cannot be destroyed nor created. Using Einstein’s equation E= mc² explain how large amounts of energy are necessary to fuse atoms together. If energy is conserved where did all this energy go?

S3.63

When large amounts of energy are used to fuse atoms together (eg: fusion) we can observe that the mass of the atoms is very small compared to the amount of energy used. However, using Einstein's equation E= mc² we see that the mass is multiplied times the speed of light squared which will result in a very large number. The energy was not destroyed but rather stored in the chemical bonds of the atoms.

Q3.64

For the nuclear process we cannot apply the assumption that \(∆_fH = 0\) for most stable elements because there are different components in the reactant and product sides. Explain this difference?

Q3.66

You eat 2 pounds of fries for lunch and the fuel value is approximately \(2.9kcal\,g^{-1}\). If you don't store any of the energy, calculate the amount of water (evaporated perspiration) needed to keep your body temperature constant.

S3.66

Step1: (Hint: Calculate the fuel value for 2 pound of fries)

\[(2\;pounds\;of\;fries)(\dfrac{454g\,fries}{1\,pound\,fries})(\dfrac{2.9kcal\,fries}{g\,fries})(\dfrac{4.184kJ}{1kcal})=1.1017\times10^4kj\]

Step 2: (Hint: Use \(\Delta _{vap}H\) to calculate grams of \(H_2O\))

\[H_2O_{(l)}\rightarrow H_2O{(g)}\]

\[\Delta _{vap}H=44.01kjmol^{-1} at\;298K\]

\[(\dfrac{1.1017\times10^4jk}{44.01kj\,mol^{-1}})(\dfrac{18.02H_2O}{1mol\,H_2O})=4.51\times10^3g\,H_2O\]

Q3.68

What is the final temperature of the following reaction:

\[C_3H_{8(g)}+5O_{2(g)} \rightarrow 3CO_{2(g)} +4H_2O_{(l)}\]

Hint: first find \(\Delta_rH^\circ\), then look up the standard molar heat capacities of the products.

S3.68

\(\begin{align*}\Delta _rH^\circ &=\sum n\Delta _fH^\circ_{product}-\sum n\Delta _fH^\circ_{reactant}\\&=3(-393.5kJ/mol)+4(-241.8kJ/mol)-(-104.6kJ/mol)-5(0kJ/mol)\\&=-2043.1kJ/mol\end{align*}\)

\(\Delta_rH^\circ=q_{p,rxn}=-q_{p,absorbed by product}= (n\bar{C}_{p,CO_2}+n\bar{C}_{p,H_2O})\Delta T\\
\Delta T=T_f-T_i=\dfrac{-q_{p,abs by prod}}{n\bar{C}_{p,CO_2}+n\bar{C}_{p,H_2O}}\)

\(\begin{align*}T_f&=T_i+\dfrac{-q_{p,abs by prod}}{n\bar{C}_{p,CO_2}+n\bar{C}_{p,H_2O}}\\
&=298.15K+\dfrac{2043.1kJ/mol}{3(37.1*10^{-3}kJ/K*mol)+4(33.6*10^{-3}kJ/K*mol)}=8613.6K\end{align*}\)

Q3.70

The reaction below is a oxidation of 2-propanol to make acetone

a) Calculate the change of enthalpy of reaction by using bond enthalpies

b) Compare the result with the reaction of the combustion 2-propanol that has an enthalpy of -1825.5 kJ/mol. What does this say about the two reactions. (Hint: Look at bond enthalpies).

S3.70

a)

Types of bonds formed	#of bonds formed	Bond Enthalpy (kJ/mol)	Enthalpy change (kJ/mol)
C-H	6	414	2484
C-C	2	347	694
C=O	1	724	724
O-H	1	460	460

\[\Delta _{r} H^{\circ} = \sum BE(reactants) - \sum BE(products) =[(2898 + 694+351+460) - (2484+694+724+460)] \frac{kJ}{mol} = {\color{red}+41 \frac{kJ}{mol}} \]

b) According to the enthalpy values, the enthalpy of the oxidation of 2-propanol into ketone is positive while its combustion is largely negative. This tells that although oxygen is involved, the two reactions are different. The combustion releases heat where as the other process needs an absorption of energy in order for the reaction to take place. In this case is usually the help of another catalyst.

Q3.71a

The molar enthalpy of sublimation for an unknown organic substance is found to be 58.05 KJ/mol, and the molar enthalpy of vaporization is 37.12 KJ/mol. Using these values, provide an estimate for the molar enthalpy of fusion for this substance.

Hint: Sublimination is the transition from solid to gas phase. Fusion and Vaporization, respectively, are the the transition from solid to liquid, then liquid to gas.

S3.71a

In general,

\[\Delta _{sub}\bar{H}^{\circ}=\Delta _{vap}\bar{H}^{\circ}+\Delta _{fus}\bar{H}^{\circ}\]

\[\Delta _{fus}\bar{H}^{\circ}=\Delta _{sub}\bar{H}^{\circ}-\Delta _{vap}\bar{H}^{\circ}=58.05\frac{KJ}{mol}-37.12\frac{KJ}{mol}=20.93\frac{KJ}{mol}\]

Q3.71b

Calculate the standard enthalpy of sublimation of ethanol. Δ_fusH^º(ethanol) = 4.9 kJ mol^-1 and Δ_vapH^º (ethanol) = 38.56 kJ mol^-1.

S3.71b

You can estimate the standard enthalpy of sublimation by adding up the standard enthalpies of fusion and vaporization since sublimation consists of two simultaneous phase changes. See here for more information on it.

Δ_subH^º(ethanol) = 4.9+38.56 = 43.46 kJ mol^-1

Q3.72

Nitric acid is neutralized by hydroxide via the reaction HNO₃ (aq) + OH^-(aq) → H₂O(l) + NO₃^-(aq). The dissociation of water has an enthalpy change of 55.8 kJ/mol. What is the enthalpy change for the dissociation of nitric acid?

Chemical	HNO3	OH^-	H2O	NO3^-
ΔfH (kJ/mol)	-207.6	-229.6	-285.8	-206.6

S3.72

The dissociation of water is H₂O(l) -> H⁺(aq) + OH^-(aq), which when added to the neutralization reaction above, gives the overall reaction

\[HNO_3 (aq) \rightarrow H^+(aq) + NO_3^-(aq)\]

which is the dissociation reaction for nitric acid. The enthalpy change of the first reaction is given by the difference in the total enthalpies of formation of the products and reactants, i.e.

Δ_rH=(-206.6 kJ/mol -285.8 kJ/mol) - (-229.6 kJ/mol -207.6 kJ/mol) = -55.2 kJ/mol.

When added to the enthalpy change for the dissociation of water to obtain the enthalpy change for the dissociation of nitric acid, we have:

Δ_netH=-55.2 kJ/mol + 55.8 kJ/mol = 0.6 kJ/mol