Bond Enthalpies
- Page ID
- 3809
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One of the most confusing things about this is the way the words are used. These days, the term "bond enthalpy" is normally used, but you will also find it described as "bond energy" - sometimes in the same article. An even older term is "bond strength". So you can take all these terms as being interchangeable.
Molecules
A diatomic molecule is one that only contains two atoms. They could be the same (for example, Cl2) or different (for example, HCl). The bond dissociation enthalpy is the energy needed to break one mole of the bond to give separated atoms - everything being in the gas state.
The point about everything being in the gas state is essential; you cannot use bond enthalpies to do calculations directly from substances starting in the liquid or solid state. As an example of bond dissociation enthalpy, to break up 1 mole of gaseous hydrogen chloride molecules into separate gaseous hydrogen and chlorine atoms takes 432 kJ. The bond dissociation enthalpy for the H-Cl bond is +432 kJ mol-1.
What happens if the molecule has several bonds, rather than just 1? Consider methane, CH4. It contains four identical C-H bonds, and it seems reasonable that they should all have the same bond enthalpy. However, if you took methane to pieces one hydrogen at a time, it needs a different amount of energy to break each of the four C-H bonds. Every time you break a hydrogen off the carbon, the environment of those left behind changes. And the strength of a bond is affected by what else is around it.
In cases like this, the bond enthalpy quoted is an average value. In the methane case, you can work out how much energy is needed to break a mole of methane gas into gaseous carbon and hydrogen atoms. That comes to +1662 kJ and involves breaking 4 moles of C-H bonds. The average bond energy is therefore +1662/4 kJ, which is +415.5 kJ per mole of bonds.
That means that many bond enthalpies are actually quoted as mean (or average) bond enthalpies, although it might not actually say so. Mean bond enthalpies are sometimes referred to as "bond enthalpy terms". In fact, tables of bond enthalpies give average values in another sense as well, particularly in organic chemistry. The bond enthalpy of, say, the C-H bond varies depending on what is around it in the molecule. So data tables use average values which will work well enough in most cases.
That means that if you use the C-H value in some calculation, you can't be sure that it exactly fits the molecule you are working with. So don't expect calculations using mean bond enthalpies to give very reliable answers. You may well have to know the difference between a bond dissociation enthalpy and a mean bond enthalpy, and you should be aware that the word mean (or average) is used in two slightly different senses. But for calculation purposes, it isn't something you need to worry about. Just use the values you are given.
Finding enthalpy changes of reaction from bond enthalpies
Case 1: Everything present is gaseous
Remember that you can only use bond enthalpies directly if everything you are working with is in the gas state.
Using the same method as for other enthalpy sums
We are going to estimate the enthalpy change of reaction for the reaction between carbon monoxide and steam. This is a part of the manufacturing process for hydrogen.
\[ CO(g) + H_2O(g) \rightarrow CO_2 (g) +H_2(g)\]
The bond enthalpies are :
| bond enthalpy (kJ mol-1) | |
|---|---|
| C≡O in carbon monoxide | +1077 |
| C-O in carbon dioxide | +805 |
| O-H | +464 |
| H-H | +436 |
So let's do the sum. Here is the cycle - make sure that you understand exactly why it is the way it is.
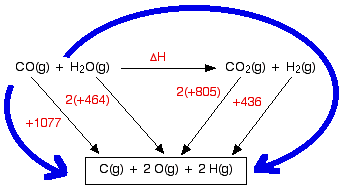
And now equate the two routes, and solve the equation to find the enthalpy change of reaction.
ΔH + 2(805) + 436 = 1077 + 2(464)
ΔH = 1077 + 2(464) - 2(805) - 436
ΔH = -41 kJ mol-1
Using a short-cut method for simple cases
You could do any bond enthalpy sum by the method above - taking the molecules completely to pieces and then remaking the bonds. If you are happy doing it that way, just go on doing it that way. However, if you are prepared to give it some thought, you can save a bit of time - although only in very simple cases where the changes in a molecule are very small.
For example, chlorine reacts with ethane to give chloroethane and hydrogen chloride gases (a ll of these are gases).

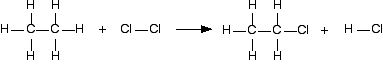
Solution
It is always a good idea to draw full structural formulae when you are doing bond enthalpy calculations. It makes it much easier to count up how many of each type of bond you have to break and make. If you look at the equation carefully, you can see what I mean by a "simple case". Hardly anything has changed in this reaction. You could work out how much energy is needed to break every bond, and how much is given out in making the new ones, but quite a lot of the time, you are just remaking the same bond.
All that has actually changed is that you have broken a C-H bond and a Cl-Cl bond, and made a new C-Cl bond and a new H-Cl bond. So you can just work those out.
Work out the energy needed to break C-H and Cl-Cl:
+413 + 243 = +656 kJ mol-1
Work out the energy released when you make C-Cl and H-Cl:
-346 - 432 = -778 kJ mol-1
So the net change is +656 - 778 = -122 kJ mol-1
Case 2: A Liquid is Present
You can only use bond enthalpies directly if everything you are working with is in the gas state. If you have one or more liquids present, you need an extra energy term to work out the enthalpy change when you convert from liquid to gas, or vice versa. That term is the enthalpy change of vaporization, and is given the symbol ΔHvap or ΔHv.
This is the enthalpy change when 1 mole of the liquid converts to gas at its boiling point with a pressure of 1 bar (100 kPa) (older sources might quote 1 atmosphere rather than 1 bar.)
For water, the enthalpy change of vaporization is +41 kJ mol-1. That means that it take 41 kJ to change 1 mole of water into steam. If 1 mole of steam condenses into water, the enthalpy change would be -41 kJ. Changing from liquid to gas needs heat; changing gas back to liquid releases exactly the same amount of heat.
You can only use bond enthalpies directly if everything you are working with is in the gas state.
To see how this fits into bond enthalpy calculations, we will estimate the enthalpy change of combustion of methane - in other words, the enthalpy change for this reaction:
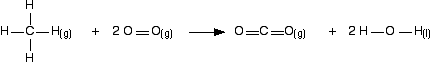
Notice that the product is liquid water. You cannot apply bond enthalpies to this. You must first convert it into steam. To do this you have to supply 41 kJ mol-1. The bond enthalpies you need are:
| bond enthalpy (kJ mol-1) | |
|---|---|
| C-H | +413 |
| O=O | +498 |
| C=O in carbon dioxide | +805 |
| O-H | +464 |
The cycle looks like this:
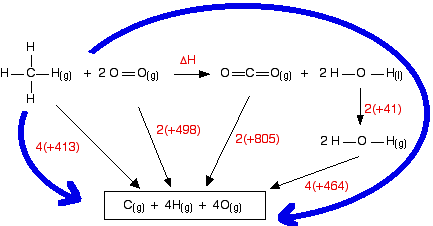
This obviously looks more confusing than the cycles we've looked at before, but apart from the extra enthalpy change of vaporization stage, it isn't really any more difficult. Before you go on, make sure that you can see why every single number and arrow on this diagram is there.
In particular, make sure that you can see why the first 4 appears in the expression "4(+464)". That is an easy thing to get wrong. (In fact, when I first drew this diagram, I carelessly wrote 2 instead of 4 at that point!) That's the hard bit done - now the calculation:
ΔH + 2(805) + 2(41) + 4(464) = 4(413) + 2(498)
ΔH = 4(413) + 2(498) - 2(805) - 2(41) - 4(464)
ΔH = -900 kJ mol-1
The measured enthalpy change of combustion is -890 kJ mol-1, and so this answer agrees to within about 1%. As bond enthalpy calculations go, that's a pretty good estimate.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


