Neutralization
- Page ID
- 1285
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A neutralization reaction is when an acid and a base react to form water and a salt and involves the combination of H+ ions and OH- ions to generate water. The neutralization of a strong acid and strong base has a pH equal to 7. The neutralization of a strong acid and weak base will have a pH of less than 7, and conversely, the resulting pH when a strong base neutralizes a weak acid will be greater than 7.
When a solution is neutralized, it means that salts are formed from equal weights of acid and base. The amount of acid needed is the amount that would give one mole of protons (H+) and the amount of base needed is the amount that would give one mole of (OH-). Because salts are formed from neutralization reactions with equivalent concentrations of weights of acids and bases: N parts of acid will always neutralize N parts of base.
| Strong Acids | Strong Bases |
|---|---|
| HCl | LiOH |
| HBr | NaOH |
| HI | KOH |
| HCIO4 | RbOH |
| HNO3 | CsOH |
| Ca(OH)2 | |
| Sr(OH)2 | |
| Ba(OH)2 |
Strong Acid-Strong Base Neutralization
Consider the reaction between \(\ce{HCl}\) and \(\ce{NaOH}\) in water:
\[\underset{acid}{HCl(aq)} + \underset{base}{NaOH_{(aq)}} \leftrightharpoons \underset{salt}{NaCl_{(aq)}} + \underset{water}{H_2O_{(l)}}\]
This can be written in terms of the ions (and canceled accordingly)
\[\ce{H^{+}(aq)} + \cancel{\ce{Cl^{-}(aq)}} + \cancel{\ce{Na^{+}(aq)}} + \ce{OH^{-} (aq)} → \cancel{\ce{Na^{+}(aq)}} + \cancel{\ce{Cl^{-}_(aq)}} + \ce{H_2O(l)}\]
When the spectator ions are removed, the net ionic equation shows the \(H^+\) and \(OH^-\) ions forming water in a strong acid, strong base reaction:
\(H^+_{(aq)} + OH^-_{(aq)} \leftrightharpoons H_2O_{(l)} \)
When a strong acid and a strong base fully neutralize, the pH is neutral. Neutral pH means that the pH is equal to 7.00 at 25 ºC. At this point of neutralization, there are equal amounts of \(OH^-\) and \(H_3O^+\). There is no excess \(NaOH\). The solution is \(NaCl\) at the equivalence point. When a strong acid completely neutralizes a strong base, the pH of the salt solution will always be 7.
Weak Acid-Weak Base Neutralization
A weak acid, weak base reaction can be shown by the net ionic equation example:
\(H^+ _{(aq)} + NH_{3(aq)} \leftrightharpoons NH^+_{4 (aq)} \)
The equivalence point of a neutralization reaction is when both the acid and the base in the reaction have been completely consumed and neither of them are in excess. When a strong acid neutralizes a weak base, the resulting solution's pH will be less than 7. When a strong base neutralizes a weak acid, the resulting solution's pH will be greater than 7.
| Strength of Acid and Base | pH Level |
|---|---|
| Strong Acid-Strong Base | 7 |
| Strong Acid-Weak Base | <7 |
| Weak Acid-Strong Base | >7 |
| Weak Acid-Weak Base | pH <7 if \(K_a > K_b\) pH =7 if \(K_a = K_b\) pH >7 if \(K_a< K_b\) |
Titration
One of the most common and widely used ways to complete a neutralization reaction is through titration. In a titration, an acid or a base is in a flask or a beaker. We will show two examples of a titration. The first will be the titration of an acid by a base. The second will be the titration of a base by an acid.
Suppose 13.00 mL of a weak acid, with a molarity of 0.1 M, is titrated with 0.1 M NaOH. How would we draw this titration curve?
Solution
Step 1: First, we need to find out where our titration curve begins. To do this, we find the initial pH of the weak acid in the beaker before any NaOH is added. This is the point where our titration curve will start. To find the initial pH, we first need the concentration of H3O+.
Set up an ICE table to find the concentration of H3O+:
| \(HX\) | \(H_2O\) | \(H_3O^+\) | \(X^-\) | |
|---|---|---|---|---|
| Initial | 0.1M | |||
| Change | -xM | +xM | +xM | |
| Equilibrium | (0.1-x)M | +xM | +xM |
\[Ka=(7)(10^{-3})\]
\[K_a=(7)(10^{-3})=\dfrac{(x^2)M}{(0.1-x)M}\]
\[x=[H_3O^+]=0.023\;M\]
Solve for pH:
\[pH=-\log_{10}[H_3O^+]=-\log_{10}(0.023)=1.64\]
Step 2: To accurately draw our titration curve, we need to calculate a data point between the starting point and the equivalence point. To do this, we solve for the pH when neutralization is 50% complete.
Solve for the moles of OH- that is added to the beaker. We can to do by first finding the volume of OH- added to the acid at half-neutralization. 50% of 13 mL= 6.5mL
Use the volume and molarity to solve for moles (6.5 mL)(0.1M)= 0.65 mmol OH-
Now, Solve for the moles of acid to be neutralized (10 mL)(0.1M)= 1 mmol HX
Set up an ICE table to determine the equilibrium concentrations of HX and X:
| \(HX\) | \(H_2O\) | \(H_3O^+\) | \(X^-\) | |
|---|---|---|---|---|
| Initial | 1 mmol | |||
| Added Base | 0.65 mmol | |||
| Change | -0.65 mmol | -0.65 mmol | -0.65 mmol | |
| Equilibrium | 0.65 mmol | 0.65 mmol |
To calculate the pH at 50% neutralization, use the Henderson-Hasselbalch approximation.
pH=pKa+log[mmol Base/mmol Acid]
pH=pKa+ log[0.65mmol/0.65mmol]
pH=pKa+log(1)
\[pH=pKa\]
Therefore, when the weak acid is 50% neutralized, pH=pKa
Step 3: Solve for the pH at the equivalence point.
The concentration of the weak acid is half of its original concentration when neutralization is complete 0.1M/2=.05M HX
Set up an ICE table to determine the concentration of OH-:
| \(HX\) | \(H_2O\) | \(H_3O^+\) | \(X^-\) | |
|---|---|---|---|---|
| Initial | 0.05 M | |||
| Change | -x M | +x M | +x M | |
| Equilibrium | 0.05-x M | +x M | +x M |
Kb=(x^2)M/(0.05-x)M
Since Kw=(Ka)(Kb), we can substitute Kw/Ka in place of Kb to get Kw/Ka=(x^2)/(.05)
\[x=[OH^-]=(2.67)(10^{-7})\]
\[pOH=-\log_{10}((2.67)(10^{-7}))=6.57\]
\[pH=14-6.57=7.43\]
Step 4: Solve for the pH after a bit more NaOH is added past the equivalence point. This will give us an accurate idea of where the pH levels off at the endpoint. The equivalence point is when 13 mL of NaOH is added to the weak acid. Let's find the pH after 14 mL is added.
Solve for the moles of OH-
\[ (14 mL)(0.1M)=1.4\; mmol OH^-\]
Solve for the moles of acid
\[(10\; mL)(0.1\;M)= 1\;mmol \;HX\]
Set up an ICE table to determine the \(OH^-\) concentration:
| \(HX\) | \(H_2O\) | \(H_3O^+\) | \(X^-\) | |
|---|---|---|---|---|
| Initial | 1 mmol | |||
| Added Base | 1.4 mmol | |||
| Change | -1 mmol | -1 mmol | 1 mmol | |
| Equilibrium | 0 mmol | 0.4 mmol | 1 mmol |
\[[OH-]=\frac{0.4\;mmol}{10\;mL+14\;mL}=0.17\;M\]
\[pOH=-log_{10}(0.17)=1.8\]
\[pH=14-1.8=12.2\]
We have now gathered sufficient information to construct our titration curve.
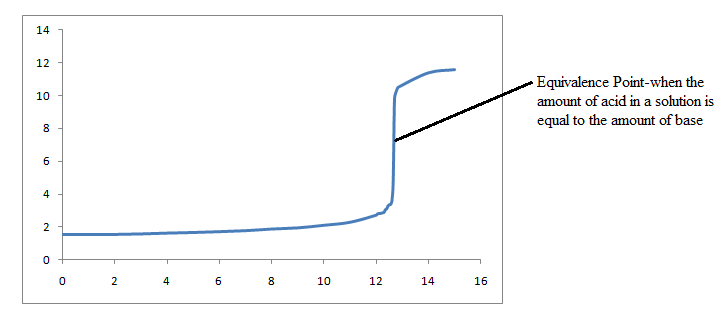
In this case, we will say that a base solution is in an Erlenmeyer flask. To neutralize this base solution, you would add an acid solution from a buret into the flask. At the beginning of the titration, before adding any acid, it is necessary to add an indicator, so that there will be a color change to signal when the equivalence point has been reached.
We can use the equivalence point to find molarity and vice versa. For example, if we know that it takes 10.5 mL of an unknown solution to neutralize 15 mL of 0.0853 M NaOH solution, we can find the molarity of the unknown solution using the following formula:
\[M_1V_1 = M_2V_2\]
where M1 is the molarity of the first solution, V1 is the volume in liters of the first solution, M2 is the molarity of the second solution, and V2 is the volume in liters of the second solution. When we plug in the values given to us into the problem, we get an equation that looks like the following:
\[(0.0835)(0.015) = M_2(0.0105)\]
After solving for M2, we see that the molarity of the unknown solution is 0.119 M. From this problem, we see that in order to neutralize 15 mL of 0.0835 M NaOH solution, 10.5 mL of the .119 M unknown solution is needed.
Problems
1. Will the salt formed from the following reaction have a pH greater than, less than, or equal to seven?
\(CH3COOH_{(aq)} + NaOH_{(s)} \leftrightharpoons Na^+ + CH3COO^- + H2O_{(l)}\)
2. How many mL of .0955 M Ba(OH)2 solution are required to titrate 45.00 mL of .0452 M HNO3?
3. Will the pH of the salt solution formed by the following chemical reaction be greater than, less than, or equal to seven?
\(NaOH + H_2SO_4 \leftrightharpoons H_2O + NaSO_4\)
4. We know that it takes 31.00 mL of an unknown solution to neutralize 25.00 mL of .135 M KOH solution. What is the molarity of the unknown solution?
Solutions
1. After looking at the net ionic equation,
\[CH_3CO_2H_{(aq)} + OH^- \leftrightharpoons CH_3COO^- + H_2O_{(l)}\]
we see that a weak acid, \(CH_3CO_2H\), is being neutralized by a strong base, \(OH^-\). By looking at the chart above, we can see that when a strong base neutralizes a weak acid, the pH level is going to be greater than 7.
2. By plugging the numbers given in the problem in the the equation:
\[M_1V_1= M_2V_2\]
we can solve for \(V_2\).
\[V_2= \dfrac{M_1V_1}{M_2} = \dfrac{(0.0452)(0.045)}{0.0955} = 21.2\; mL\]
Therefore it takes 21.2 mL of \(Ba(OH)_2\) to titrate 45.00 mL \(HNO_3\).
3. We know that NaOH is a strong base and H2SO4 is a strong acid. Therefore, we know the pH of the salt will be equal to 7.
4. By plugging the numbers given in the problem into the equation:
\[M_1V_2 = M_2V_2\]
we can solve for M2.
(0.135)(0.025) = M2(0.031)
M2 = 0.108 M. Therefore, the molarity of the unknown solution is .108 M.
References
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2007.
- Criddle, Craig and Larry Gonick. The Cartoon Guide to Chemistry. New York: HarperCollins Publishers, 2005.
Contributors and Attributions
- Katherine Dunn (UCD), Carlynn Chappell (UCD)

