2.E: Properties of Gases (Exercises)
- Page ID
- 41328
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.5: Condensation of Gases and the Critical State
Q2.2
There are some gases in existence, such as \(\ce{NS2}\) and \(\ce{NCl2}\), which do not follow Boyle's Law, regardless of the pressure conditions they're under. Explain why this is the case.
S2.2
Boyle's Law assumes that the only factors changing are pressure (\(P\)) and volume (\(V\)), therefore, in order to apply Boyle's Law, both number of molecules (\(n\)) and temperature (\(T\)) must remain constant. However, both \(NS_2\) and \(NCl_2\) do not have constant \(n\) because they undergo association reactions when in contact with like molecules.
\[ 2NH_2 \rightleftharpoons N_2S_2\]
\[ 2NCl_2 \rightleftharpoons N_2Cl_2\]
Therefore, Boyle's Law may not be applied for these gases.
Q2.3
An ideal gas originally at 0.85 atm and 66ºC was allowed to expand until its final volume, pressure, and temperature were 94 mL, 0.60 atm, and 45ºC, respectively. What was its initial volume?
S2.3
- \(P_1=0.85\;atm\)
- \(T_1=339\;K\)
- \({V_2=94\;mL}\)
- \(P_2=0.60\;atm\)
- \(T_2=318\;K\)
\[V_1=\dfrac{(P_2)(V_2)(T_1)}{(T_2)(P_1)}\]
\[=\dfrac{(0.60\;atm)(94\;mL)(339\;K)}{(318\;K)(0.85\;atm)}=71\;mL\]
Q2.4
Some ballpoint pens have a small hole in the main body of the pen. What is the purpose of the hole?
S2.4
The hole is there to allow the pressure to equalize and allow the ink to flow out of the pen.
Q2.5
Starting with the ideal-gas equation, show how you ca calculate the molar mass of a gas from a knowledge of its density
S2.5
Q2.6
At STP (standard temperature and pressure), 0.280 /;L of a gas weighs 0.400/;g. Calculate the molar mass of the gas.
S2.6
First, we need to determine the moles of gas in the sample:
\[n=\dfrac{(P)(V)}{(R)(T)}\]
\[=\dfrac{(1.00\;atm)(0.280\;L)}{(0.08206\;L-atm/mol-K)(273\;K)}=0.0125\;moL\]
\[=\dfrac{(0.400\;g)}{(0.0125\;mol)}=32.0\;g/moL\]
Q2.7
Ozone molecules in the stratosphere absorb much of the harmful radiation from the sun. Typically, the temperature and partial pressure of ozone in the stratosphere are 250 K and 0.0010 atm, respectively. How many ozone molecules are present in 1.0 L of air under these conditions? Assume ideal-gas behavior.
Q2.9
Dissolving 3.00 g of an impure sample of CaCO3 in an excess of HCl acid produced 0.656 L of CO2 (measured at 20ºC and 792 mmHg). Calculate the percent by mass of CaCO3 in the sample.
Q2.14
- What volume of air at 1.0 atm and 22ºC is needed to fill a 0.98 L bicycle tire to a pressure of 5.0 atm at the same temperature? (Note that the 5.0 atm is the gauge pressure, which is the difference between the pressure in the tire and the atmospheric pressure. Initially, the gauge pressure in the tire was 0 atm.)
- What is the total pressure in the tire when the gauge reads 5.0 atm?
- The tire is pumped with a hand pump full of air at 1.0 atm; compressing the gas in the cylinder adds all of the air in the pump to the air in the tire. If the volume of the pump is 33% of the tire's volume, what is the gauge pressure in the tire after 2 full strokes of the pump?
Q2.15
A student breaks a thermometer and spills most of the mercury (Hg) onto the floor of a laboratory that measures 15.2 m long, 6.6 m wide, and 2.4 m high. The vapor pressure of mercury at 20ºC is 1.7 x 10-6 atm.
- Calculate the mass of mercury vapor (in grams)in the room at 20ºC.
- Does the concentration of mercury vapor exceed the air quality regulation of 0.050 mm Hg m-3 of air?
- One way to treat small quantities of spilled mercury is to spray powdered sulfur over the metal. Suggest a physical and a chemical reason for this treatment.
S2.15
a) The volume of the room is 15.2 m x 6.6 m x 2.4 m = 240 m3.
The pressure is 1.7 x 10-6 atm x 101325 Pa/atm = 0.17 Pa
Ideal gas equation:
\[ PV=nRT\]
\[n=\dfrac{PV}{RT}\]
\[n=\dfrac{0.17\;Pa*(240)\;m^3}{\dfrac{8.314\;Pa-m^3}{K-mol}*(293K)}\]
\[=0.017\;mole\]
Mass of mercury vapor : mHg = nHg * MHg =(0.017 mole)(200.6 g/mole)(1000 mg/gram)} = 3400 mg
b) The mass density of mercury vapor :
[Hg] = mHg / VHg(l) = \[\dfrac{3400\;mg}{240\;m^{-3}}\]
=14 mg/m3
This value is indeed larger than the 0.050 mg Hg m-3 allowed.
c) Using powdered sulfur to absorb the spilled mercury works because the sulfur molecules will strongly bind to the mercury, and the mercury sulfide that forms is a solid. This makes removing spilled mercury (a liquid) easier.
Q2.16
An oxide has the density of 1.75 g L-1 at 1.12 atm and 100ºC. Is this oxide O2(g) or O3(g)?
S2.16
\[M = \dfrac{\rho RT}{P} \]
\[= \dfrac{(1.75 g L^{-1})(0.08206 L atm K^{-1}mol^{-1})(100+273)K)}{1.12 atm}=47.8 \dfrac{g}{mol}\]
The molar mass of O3(g) is 48 g mol-1, so the oxide must be O3(g)
Q2.21
You are given a gas at 750 torr with a volume of 0.62 Liters at 25°C. A while later, you measure the temperature and notice a 5°C temperature increase in the system. Assuming there is no pressure change and that this is an ideal gas, what is the new volume?
S2.21
First: List out what you have
.gif?revision=1&size=bestfit&width=276&height=39)
Vi=0.62 L
Ti=25ºC +273.15= 298.15
We do not know the amount of moles so we should find that.
PV=nRT
.gif?revision=1&size=bestfit&width=247&height=46)
So ni=2.47x10-4 moles
Pf=0.987 atm
Vf=?
Tf=298.15 K + 5 K= 303.15 K
Vf=(nRT)/P
.gif?revision=1&size=bestfit&width=315&height=46)
=0.631 L
Q2.23a
The composition of air in your alveoli is 75% N2, 14% O2, 5% CO2, and 6% H2O, by volume. (a) Calculate the average molar mass of this air sample. (b) Calculate the partial pressures of N2, O2, CO2, and H2O in your alveoli. assuming that alveolar pressure is 760 torr (At constant pressure and temperature, the volume of a gas is directly proportional to the number of moles of gas).
Q2.23b
The composition of air in your alveoli is 75% N2, 14% O2, 5% CO2, and 6% H2O, by volume. (a) Calculate the average molar mass of this air sample. (b) Calculate the partial pressures of N2, O2, CO2, and H2O in your alveoli. (At constant pressure and temperature, the volume of a gas is directly proportional to the number of moles of gas.)
Q2.24
In an expandable balloon we find a mixture of two gases only. The mass percent of the gases are: 65% 02 and 35 % HQ2. The mass of the gases combined is 4.6 grams. Calculate the total volume these two gases occupy at 298 K and 1.00 atm.
S2.24
You can find the Volume by using the Ideal Gas Law equation:
\[V=\dfrac{nRT}{P}\]
The mass of the two gases is given by:
\( m_{H_{2}}= 4.6\times 0.35=1.6g\)
\(m_{O_{2}}= 4.6\times 0.65=3.0g\)
The number of moles of the mixture= \(n_{total}=n_{H_{2}}+n_{O_{2}}\)
\( n_{total}=\dfrac{1.60g}{Q2.0g.mol^{-1}}+\dfrac{3.0g}{32g.mol^{-1}}=0.884mol\)
The volume the two gases occupy = \(V=\dfrac{(0.884mol)(0.08206\dfrac{L.atm}{K.mol})(298K)}{1.0 atm}= 21.6 L\)
Q2.25
The temperature in a small room in summer time is 31oC. The room (dimension 4mx4mx3m) is filled with 0.88 kg of water vapor. What is the partial pressure of water vapor in the air?
Q2.27
A flask contains a mixture of two ideal gases, A and B. Show graphically how the total pressure of the system depends on the amount of A present. That is, plot the total pressure versus the mole fraction of A. Do the same for B on the same graph. The total number of moles of A and B is remained as constant.
S2.27

Q2.29
When you drink something from a straw, how does the liquid get from the glass up through the straw into your mouth?
S2.29
When you close your mouth around the straw, you close off the atmosphere from outside to inside. During suction, you increase the volume inside your mouth, thus lowering the internal pressure and the atmospheric pressure exerted onto the liquid over comes the internal pressure and so the liquid flows into your mouth.
Q2.31
Consider the reaction of ferrous sulfide with a dilute acid:
\[FeS_{(s)} + 2HCl_{(aq)} \rightarrow H_2S_{(g)} + FeCl_{2(l)}\]
An amount of 5.10 grams of ferrous sulfide completely reacted in this reaction. The gas collected over the water at 27ºC has a volume 1.78 L. Find the pressure of the collected gas in atm. The vapor pressure of water at 27°C is 26.7 mmHg.
Hint: Look at Dalton's law of partial pressure
S2.31
Base on the amount of reactant, use stoichiometry to find the number of moles of H2S gas produced and get partial pressure of hydrogen sulfide gas. Then use Dalton's law of partial pressure to find the total pressure of collected gas.
\[ 5.10g FeS \times \dfrac{1mole FeS}{87.92g FeS} \times \dfrac{1mole H_{2}S}{1mole FeS} = 0.058mole H_{2}S\]
\[ P_{H_{2}S} = \dfrac{nRT}{V} = \dfrac{0.058 mole H_{2}S\times0.08206 \dfrac{L\cdot atm}{mole\cdot K}\times(27+273)K}{1.78 L} = 0.802 atm\]
\[ P_{total} = P_{H_{2}S} + P_{H_{2}O} = 0.802 atm + (26.7 mmHg \times \dfrac{1atm}{760mmHg}) = {\color{red} 0.837 atm} \]
Q2.32a
Tanks containing mixtures of oxygen and nitrogen are routinely lowered to the Aquarius underwater research lab in Florida. What is the percent composition of oxygen gas in the tank if the total pressure in the tank once it has reached Aquarius is 6.5 atm, and the partial pressure is 0.55 atm?
S2.32a
For any ideal gas,
\[PV=nRT\]
At constant pressure and temperature, V is proportional to n. Thus:
\[P_{O^{2}}=x_{O^{2}}P_{total}\]
\[x_{O^{2}}=\dfrac{P_{O^{2}}}{P_{total}}=\dfrac{0.55atm}{6.5atm}=.085\]
The percent composition is 8.5%
Q2.32b
A mixture of helium and oxygen gas is used to fill up an apparatus. If the total pressure within the apparatus is 10 atm and the partial pressure of helium is 2 atm within that apparatus, calculate the percent by volume of diatomic oxygen gas.
S2.32b
\[ \chi_{He}=\frac{P_{He}}{P_{total} }, \ where \ \chi = Mole \ Fraction\]
\[ \begin{align*} \chi_{He} &= \frac{2 atm}{10 atm} \\ \chi_{He} &= 0.2 \end{align*}\]
\[ \begin{align*} \% \ by \ volume \ He &= \chi_{He} \cdot 100 \\ &= 0.2\ \cdot 100= 20\%\ \end{align*}\]
\[ 100\% \ by \ volume \ total \ gas - 20\% \ by \ volume \ He= \ \underline{80\% \ by \ volume \ O_{2}}\]
Click here for more on mole fractions.
Q2.33
An unknown mass of NO2 in a closed chamber decomposes completely to oxygen and nitrogen gases. The final pressure in the chamber is 0.687 atm. What are the partial pressures of each component of the gas mixture in the chamber?
S2.33
Every two moles of NO2 produce one mole of N2 and O2. By the ideal gas equation, since we know that the gases are at the same temperature and occupy the same volume, the pressure of each gas is proportional to the number of moles of that gas present, and thus the pressure of each gas is proportional to the mole fractions of that gas. Because NO2 represents 1/3 of the total moles of gas present, and O2 represents 2/3 of the total gas present, NO2 represents 1/3 of the total pressure, and O2 represents 2/3 of the total pressure.
- PN2 = 1/3 * 0.687 atm = 0.229 atm
- PO2 = 2/3 * 0.687 atm = 0.458 atm
Q2.41
Choose the more ideal system
- H2O at 110 °C and 1 atm vs H2O at 100°C and I atm
- Cl2 at 10 atm vs Cl2 at 0.5 atm
- N2 at 60 °C vs N2 at 100°C
2.6: Kinetic Theory of Gases
Q2.41
List the ideal conditions (the conditions that help allow a gas to behave ideally).
S2.41
Ideal conditions come from the kinetic theory of gases. This theory relies on three primary assumptions (as follows):
- The gas is made up of a large amount of molecules. These molecules obey Newton's laws pertaining to motion and are always moving around in random motion.
- In comparison to the volume of the gas, the volume of the molecules are so negligible that they can essentially be ignored.
- No forces are capable of acting on the molecules except for extremely short durations of elastic collisions.
Ideal conditions are at:
- high temperatures, and
- low pressures
This is because at these conditions is when there are relatively large distance between molecules.
Q2.42
1.00 mole of an unknown gas occupies a 0.865 L container at 0.90 atm and 25ºC. If the value of van der Waals constant a= 0.550, what is the value of b for the gas? What does the value of b indicate about the gas?
S2.42
\[P=4.0atm\\V=0.70L\\T=77.2K\\a=2.50\dfrac{atm\cdot L^2}{mol^2}\]
\[(P+\dfrac{a n^2}{V^2})(V-nb)=nRT\rightarrow b=\dfrac{nRT}{P+\dfrac{an^2}{V^2}}-V(\dfrac{1}{-1})\]
\[b=\dfrac{(1mol)(.08206\dfrac{L\cdot atm}{mol\cdot K})(77.2K)}{4.0atm+\dfrac{(Q2.5)1mol^2}{.70L^2}}-.70L(\dfrac{1}{-1mol})\\=4\times 10^-3\dfrac{L}{mol}\]
The small value of \(b\) indicates that the gas molecules have a small molecular mass.
Q2.48
The compressibility for compound 1 is 0.84 and 0.56 for compound. Which compound will occupy a smaller volume?
S2.48
Z is a prediction of the behavior of gases. A smaller value means that there are stronger intermolecular forces amongst the molecules, meaning a smaller volume occupied. Therefore, compound 2 will occupy a smaller volume than compound 1.
Q2.50
True or false: The concept of temperature is a macroscopic. Explain your reasoning.
S2.50
True. The kinetic theory of gases hypothesizes that it deals with an extremely large amount of molecules. Therefore, temperature is a macroscopic concept since the average kinetic energy of the molecules within a given system is proportional to the temperature. A large amount of molecules must be included into this average in order for it to be properly utilized.
Q2.51
What assumptions are made when applying the kinetic molecular theory to gases? Are all of these assumptions necessary? Why or why not?
S2.51
There are five assumptions made when applying the kinetic molecular theory to gases are:
- Gases consist of a large amount of atoms or molecules and these atoms/ molecules have spaces of separation between them that are much larger than their size.
- Although the molecules have mass, we treat them as if they do not since their volume is negligibly small.
- The molecules are always moving around randomly.
- All collisions, both molecule-molecule collisions and molecule-wall collisions, are considered to be elastic rather than inelastic.
- The molecules are not considered to be attracted nor repulsed to/ by one another.
Most of these assumptions are in fact necessary to consider when applying the kinetic molecular theory to gases, however, assumption number 4 is not always crucial. This is due to the fact that it does not matter whether or not the collisions between the molecules and the walls are elastic if the walls of the container are at the same temperature as the molecules inside of the the container (i.e. the gas) because although kinetic energy may be transferred from molecule to molecule, it will not be converted into any other forms of energy.
Q2.52
A 3.50 L cube-shaped container container 3.5x1023 molecules of \(N_2\) at 30ºC. What is pressure exerted on one wall?
S2.52
\[N=3.5\times 10^{23}\\V=3.50L\\T=303K\\k_B=1.38\times 10^{-23} \]
\[ P=\dfrac{2N}{3V}\overline{E}_trans\rightarrow P=\dfrac{2N}{3V}(\dfrac{3}{2}k_BT)\]
\[=\dfrac{2(3.5\times 10^{23})}{3(3.50L)}[\dfrac{3}{2}(1.38\times 10^{-23})(303K)]\]
\[=4.18\times 10^2atm\]
Q2.53
Imagine a container with walls 123 cm³. Argon (with a speed of 700 m/s) atoms at 300 K are colliding at right angles with the container's walls at a rate of \(5.0 \times 10^{20} m/s\). What would the force and pressure exerted on the container's walls be?
2.7: The Maxwell Distribution Laws
Q2.54
Calculate the root-mean-square speed and the molar kinetic energy of N2 at 25oC
S2.54
The root-mean-square speed of \(N_2\) is:
\[v_{rms} = \sqrt{\dfrac{3k_BT}{m}}\]
or in terms of molar mass \(M\) instead of molecular mass (\(m\))
\[v_{rms} = \sqrt{\dfrac{3RT}{M}}\]
\[ =\sqrt{\dfrac{(3)(8.3145 \, J\,\cancel{K} \cancel{mol^{-1}})(298.15\; \cancel{K})}{ 28.02 \; \cancel{g} \, \cancel{mol^{-1}} \frac{1\; kg}{1000\; \cancel;{g}} }} = 5.15\; m/s\]
The molar kinetic energy of \(N_2\) at 25oC is:
= \(\dfrac{3}{2}*\dfrac{8.3145J}{K mol}*298.15K*\dfrac{1kJ}{1000J}\)
= 3.72 kJ/mol
Q2.55
Find the \(v_{rms}\) of N_{2(g)} at 25ºC. What temperature must \(Cl_{2(g)}\) be to have the same \(v_{rms}\)?
S2.55
\[v{_{rms}} = \sqrt{\dfrac{3 R T}{M}}\]
\[v_{rmsN_{2}} = \sqrt{\dfrac{3(8.314 J\cdot K^{-1}\cdot mol^{-1})(25+273)K}{28.02 x 10^{-3} kg\cdot mol^{-1}}}=515m \ s^{-1}\]
\[ since \ v_{rmsN_{2}} = v_{rmsCl_{2}}, then \ v_{rmsCl_{2}} = 515m \ s^{-1}\]
\[v_{rmsCl_{2}} = \sqrt{\dfrac{3(8.314 J\cdot K^{-1}\cdot mol^{-1})(T)}{70.9x10^{-3} g\cdot mol^{-1}}} = 515m \ s^{-1}\]
T = 754 K
Therefore, Cl2(g) must be 754 K to have the same vrms as N2(g) at 298 K
Q2.60
- Plot the distribution of speeds for Cl2 at 100 K, 300 K, 600 K, and 1000 K.
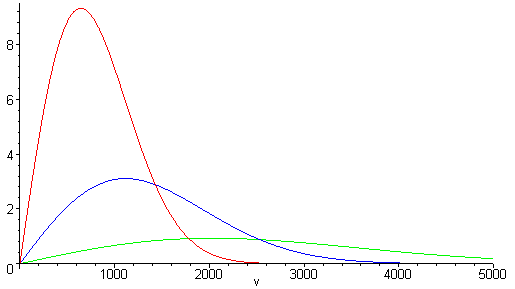
- Plot the distribution of speeds for three gases: N2, Cl2, and CH4 at the same temperature.
S2.60
a) The plot of the distribution of speeds for Cl2 at 100 K, 300 K, 600 K, and 1000 K
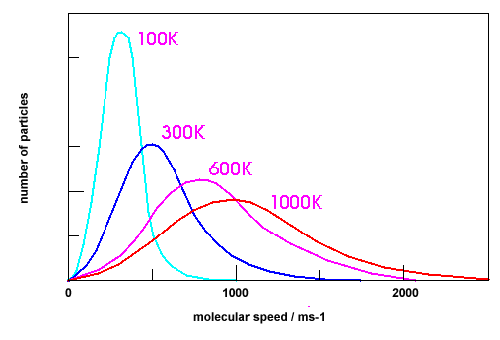
b) The plot of the distribution of N2,Cl2 and CH4 at the same temperature (300K)
Q2.60
Which gas would you expect to move faster at 255K, O2 or I2? And why?
S2.60
We'd expect O2 to move faster. This is because it is lighter. Think of the formula for average speed because it is divided by kg/mol the smaller the mass, the faster it goes.
Q2.61
According to the Maxwell speed distribution, would \(O_{2(g)}\) have a wider speed distribution at 200 K or 1000 K?
S2.61
At lower temperatures, the speed distribution will be narrower and there will will be a smaller most probable speed while the higher temperature will have a wider speed distribution and a higher most probable speed. Therefore, \(O_{2(g)}\) will have a wider speed distribution at 1000 K.
Q2.62a
A CO2 molecule at unknown temperature at sea level is released to travel upward. Assuming that the temperature is constant and that the molecule doesn’t collide with another molecules and reaches a terminal height of 8.5 meters above sea level, what is the temperature? Do the same calculation for a H2 atom. [Hint: To calculate the altitude, h, the molecule will travel, equate its kinetic energy with the potential energy, mgh, where m is the mass and g is the acceleration due to gravity (9.81 m s-2).]
Q2.62b
A CO2 molecule at unknown temperature at sea level is released to travel upward. Assuming that the temperature is constant and that the molecule doesn’t collide with another molecules and reaches a terminal height of 5000 meters above sea level, what is the temperature? Do the same calculation for a H2 atom. [Hint: To calculate the altitude, h, the molecule will travel, equate its kinetic energy with the potential energy, mgh, where m is the mass and g is the acceleration due to gravity (9.81 m s-2).]
Q2.63
Calculate the root-mean-square speed in cm/s for the following particles (hint, what is the average speed?): 0.010, 0.043, 0.027, 0.012, 0.041, 0.023, 0.011, 0.004, 0.007, and 0.009 (all in m/s).
Q2.63
The root-mean-square speed of 6 particles is 2.47 ms-1. The speed of 5 of the particles are 1.0, 2, 1.5, 3.0 and Q2.5. Calculate the unknown speed of the 6th particle. Find the average speed of the 6 particles.
S2.63
The root-mean-square of the ensemble of particles is
\[v_{rms}=\sqrt{\dfrac{\sum_{i=1}^{6} c^{2}_{i}}{m}}\]
\[2.47=\sqrt{\dfrac{1.0^{2}+Q2.0^{2}+1.5^{2}+3.0^{2}+2.5^{2}+c_{6}}{6}}\]
We solve for \(c_{6}\) and we get
\[c^{2}_{6}=(Q2.47ms^{-1})^{2}(6)-(1.0^{2}+2.0^{2}+1.5^{2}+3.0^{2}+2.5^{2}) \; m^{2}s^{-2}\]
\[c^{2}_{6}= 36.6m^{2}s^{-2}-22.5m^{2}s^{-2}\]
\[c^{2}_{6}=14.1m^{2}s^{-2}\]
\[c_{6}= 3.75ms^{-1}\]
The average speed of the 6 particles is
\[\bar{c}=\dfrac{\sum^{6}_{i=1}c_{i} }{N}\]
\[\bar{c}=\dfrac{(1.0+Q2.0+1.5+3.0+Q2.5+3.75)ms^{-1}}{6}\]
\[=2.30ms^{-1}\]
Q2.64a
Compare the velocities of Oxygen and Hydrogen at room temperature (25oC) by computing their root mean square speed?
Q2.64b
The speeds of six gaseous molecules at a given temperature are 1.0m/s , 1.2m/s, 1.5m/s, 1.7m/s, 2.0m/s, and 2.3m/s.
- Compare the root-mean-square (rms) speeds and the average speed of those molecules.
- Is always the average speed of the molecules the smaller of the two? Explain.
S2.64b
a) The root-mean-square-speed of those gases:
\[v_{rms} = \sqrt{\dfrac{1}{N}*(v_1^{2}+v2^{2}+v_3^{2}+v_4^{2}+v_5^{2}+v_6^{2})}\]
\[= \sqrt{\dfrac{1}{N}*(1^{2}+1.2^{2}+1.5^{2}+1.7^{2}+2^{2}+2.3^{2})}\]
\[ = 1.68\; m/s\]
The average speed is :
\[v_{avg} = \dfrac{1+1.2+1.5+1.7+2+2.3}{6}\]
\[ = 1.62\; m/s\]
b) The average speed is always smaller then the root-mean-square speed because the average speed depends on the temperature, rather than the molecular sizes.
Q2.65
Calculate cmp for a sample of N2(g) at 500K.
S2.65
\[c{_{mp}} = \sqrt{\dfrac{2RT}{M}}\]
\[c{_{mp}} = \sqrt{\dfrac{2 \ (8.314 J \ K^{-1} \ mol^{-1}) (500K)}{.02802 kg \ mol^{-1}}} = 545 m \ s^{-1}\]
Q2.66
Using the initial equation \(f(c)=4\pi c^2 \dfrac{m}{\pi K_BT} ^{3/2} e^{-\dfrac{mc^2}{2K_BT}}\) derive an expression for \(c_{mp}\)
S2.66
Step 1: $$f(c)=4\pi c^2 \dfrac{m}{\pi K_BT} ^{3/2} e^{-\dfrac{mc^2}{2K_BT}}\]
$$=c^2 \dfrac{m}{\pi K_BT} ^{3/2} e^{-\dfrac{mc^2}{2K_BT}}\]
Step 2: (Hint: Apply the chain rule to \(c^2\) and \(e^{-\dfrac{mc^2}{2K_BT}}\))
\[\dfrac{df(c)}{dc}=4\pi \dfrac{m}{2\pi K_BT}^{3/2} [2ce^{-\dfrac{mc^2}{2K_BT}} + c^2e^{-\dfrac{mc^2}{2K_BT}}-{\dfrac{mc}{2K_BT}}]\]
Step 3:
\[4\pi(\dfrac{m}{2\pi K_BT})^{3/2}ce^{-\dfrac{mc^2}{2K_BT}}(2-\dfrac{mc^2}{K_BT})\]
Step 4: (Hint: Set \(\dfrac{df(c)}{dc}=0\) , \(c=c_{mp}\))
\[\pi (\dfrac{m}{2\pi K_BT})^{3/2}c_{mp}e^{-\dfrac{mc_{mp}^2}{2K_BT}}(2-\dfrac{mc_{mp}^2}{K_BT})=0\]
Step 5:
\[2-\dfrac{mc^2 _{mp}}{K_BT}=0\]
Step 6:
\[c^2_{mp}=\dfrac{2K_BT}{m}\]
Step 7: (Hint: Use Avogadro's number)
\[c^2 _{mp}=\dfrac{2K_BT}{m}\dfrac{N_A}{N_A}=\dfrac{2RT}{M}\]
Step 8:
\[c_{mp}=\sqrt {\dfrac{2RT}{M}}\]
Q2.68a
Calculate the value of cmp for CH3OH at 30°C. What is the ratio of the number of molecules of speed 400 m s-1 to the number of molecules of speed cmp?
Q2.68b
Calculate the value of the most probable speed, average speed, and the root-mean-square speed for \(C_5H_{12}\) at 25°C.
S2.68b
\[c_{mp}=\sqrt{\dfrac{2RT}{M}}=\sqrt{\dfrac{2(8.314J/K*mol)(298.15K)}{72.15\times 10^{-3}kg/mol}}=26Q2.13m/s\]
\[\begin{align*}\bar{c}&=\sqrt{\dfrac{8RT}{\pi *M}}=\sqrt{\dfrac{4}{\pi}}*\sqrt{\dfrac{2RT}{M}}=\sqrt{\dfrac{4}{\pi}}*c_{mp}\\&=\sqrt{\dfrac{4}{3.14159}}*262.13\;m/s=295.78m/s\end{align*}\]
\[\begin{align*}c_{rmp}&=\sqrt{\dfrac{3RT}{M}}=\sqrt{\dfrac{3}{2}}*\sqrt{\dfrac{2RT}{M}}=\sqrt{\dfrac{3}{2}}*c_{mp}\\&=\sqrt{\dfrac{3}{2}}*262.13\; m/s=321.04\; m/s\end{align*}\]
Q2.68
Calculate the value of cmp for CH3OH at 30°C. What is the ratio of the number of molecules of speed 400 m s-1 to the number of molecules of speed cmp?
2.8: Molecular Collisions and the Mean Free Path
Q2.69
You open a container that has 1 mole of Neon gas and 1 mole of hydrogen gas. Hydrogen gas moves at faster speeds than Neon.
- Compare the mean free path between the two gases in a closed room.
- Assume travels across the room and there are no collision between molecules. Which gas reaches the other end first?
S2.69
- The Neon gas molecules are larger than the Hydrogen gas molecules. This decreases the distance the molecules have to travel before they run into each other. For this reason, the mean free path for Neon will be lower than the mean free path for Hydrogen.
- Since there are no collisions between molecules the mean free path does not play a role in this case. Therefore, Hydrogen will reach the other end first because it travels faster than Neon.
Q2.70a
How many times is the average distance between collision for a gas molecule larger than its molecular diameter, given that Pressure
Po= 780mm Hg, and temperature T=300K, molecular diameter is 2x10-10 meters.
Q2.70b
The mean free path of gas molecules is given as: \[ \gamma = \dfrac{1}{\sqrt{2}\pi d^{2}(N/V)} \]
- rewrite the equation so that the mean free path is expressed in terms of gas pressure
- Name some that factors affect this property directly and indirectly?
- Consider a gas piston containing only hydrogen gas. While not changing the temperature, there observed to be an increase in the mean free path of the gas molecules. What action could have caused this to happen?
Hint: Look at concept of mean free path
S2.70b
Mean free path is the average distance molecules traveled between each successive collision. Think of what could have affect this distance
a) \[ PV = nRT \Rightarrow V = \dfrac{nRT}{P} \]
\[ N/V = \dfrac{N}{n} \dfrac{P}{RT}\]
\[ but (N/n) = N_{A} \]
\[ \Rightarrow \dfrac{N}{V} = \dfrac{PN_{A}}{RT} \Rightarrow {\color{red} \gamma= \dfrac{RT}{\sqrt2 \pi d^{2} PN_{A}}} \]
b) direct factors: density and molecule's dameter, indirect factors: temperature, pressure, volume
c) An increase in mean free path means that the collisions are happen less frequently, therefore the density of the gas decreased. An action that could have caused this to happen is an increase in volume. A larger volume while molecules while not changing the number of molecules and speed lead to molecules are further apart and have less collisions.
Q2.70c
Gas A has a density of 0.835 g/cm3 and Gas B has a density of 14.67 g/cm3. From just this information, which do you expect to have a larger mean free path? Explain why.
S2.70c
We would expect gas A to have a larger mean free path.
Q2.71
A cylinder contains 25 molecules of an unknown ideal gas. What is the mean free path of the gas molecules? The cylinder has a volume of 20.0 cm3 and the gas has an atomic radius of 1.24 Å. (1 cm = 108 Å)
S2.71
For an ideal gas, the mean free path is calculated by:
\[\lambda =\frac{\bar{c}}{Z_{1}}=\frac{1}{\sqrt{2}\pi d^{2}\frac{N}{V}}\]
Thus, the mean free path of the unknown gas is:
\[\lambda =\frac{1}{\sqrt{2}\pi (1.24\times 10^{8}\, cm)^{2}\, \frac{25}{20.0 cm^{2}}}=1.17\times 10^{-17}cm=1.17\times 10^{-19}m\]
Q2.71
A rattle containing 50 spherical beads is shaken around by a toddler. What is the mean free path of the beads if the volume of the rattle is 500 cm3 and the diameter of each individual bead is 0.2 cm?
S2.71
Use the appropriate equation and plug in given values.
\[ \begin{align} & \lambda = \frac{1}{\sqrt{2} \pi d^{2}(N/V)} \\ & \lambda = \frac{1}{\sqrt{2} \pi (\frac{0.2}{100} m)^{2}(50 beads/\frac{500}{100}m^{3})} \\ & \underline{ \lambda = 1.8 \cdot 10^{-4} \ \ m } \end{align}\]
Click here for more details about mean free path.
Q2.72a
Calculate the mean free path and the binary number of collisions per liter per second between Ar molecules at 298 K and 1.00 atm. Use 3.62 Å as the collision diameter of the Ar molecules. Assume ideal gas behavior.
Q2.72b
Calculate the mean free path and the binary number of collisions per liter per second between Ar molecules at 298 K and 1.00 atm. Use 3.62 Å as the collision diameter of the Ar molecules. Assume ideal gas behavior.
Q2.72c
\(CO_2\) has a collision diameter of 0.4 nanometers. At 25 oC and 1.2 atm pressure, what is the mean free path between binary collisions, and what is the rate of binary collisions per liter assuming the volume contains only pure carbon dioxide gas behaving ideally?
Q2.72d
For the molecules HCl at 350K and 1.21 atm, calculate the mean free path and the binary number of collisions per liter per second. The collision diameter of HCl molecules is 5.50 Å. Assume the HCl acts as an ideal gas.
S2.72d
Step 1:
Calculate \(\dfrac{N}{V}\) to calculate the mean free path
$$PV=NRT=\dfrac{N}{N_A}RT\]
Step 2:
$$\dfrac{N}{V}=\dfrac{PN_A}{RT}=\dfrac{(1.21atm)(6.022\times 10^{23}mol^{-1})}{(0.08206L\,atm\,K^{-1}mol^{-1})(350K)}=Q2.537\]
Step 3:
Turn L into \(m^{-3}\)
$$Q2.537\times 10^{22}L^{-1}(\dfrac{1000L}{1m^{3}})=Q2.537\times 10^{22}m^{-3}\]
Step 4:
$$\lambda=\dfrac{1}{\sqrt{2}\pi d^{2}(\dfrac{N}{V})}=\dfrac{1}{\sqrt{2}\pi (5.50\times 10^{-10}m)^{2}(Q2.537\times 10^{22}m^{-3})}=Q2.93\times 10^{-5}m\]
Calculating the binary number of collisions
Step 1: (Hint: Use the equation for average molecular speed.)
$$\bar{C}=\sqrt{\dfrac{8RT}{\pi M}}=\sqrt{\dfrac{8(8.3145JK^{-1}mol^{-1}(300K)}{\pi (36.46\times 10^{-3}\dfrac{kg}{mol})}}\]
Step 2:
$$z_{11}=\sqrt{\dfrac{2}{2}}\pi d^2\bar{C}\dfrac{N}{V}^{2}\]
$$=1.80526\times 10^{29}m^{-3}s^{-1}\]
Step 3: (Hint: Turn into \(L^{-1}s^{-1}\))
$$z_{11}=\sqrt{\dfrac{2}{2}}\pi (5.50\times 10^{-10}m)^{2}(417.39ms^{-1})(\dfrac{1m^{3}}{1000L})=1.80527\times^{26} L^{-1}s^{-1}\]
Q2.73
In a 4L container you have 5 grams of 0Q2. Assume the collision diameter of 02 is 3.55 Angstrongs . Calculate the mean free path of the gas.
S2.73
The mean free path is given by
\[\lambda =\dfrac{1}{\sqrt{2}\pi d^{2}(\dfrac{N}{V})}\]
V is given and we can find \(\left ( \dfrac{N}{V} \right)\) by calculating N.
\[N=N_{A}.n=(6.022\times 10^{23}mol^{-1})(5gO_{2})(\dfrac{1mol}{32gO_{2}})\]
\[ N=9.40\times 10^{22}\]
\[\left ( \dfrac{N}{V} \right )=\dfrac{9.41\times 10^{22}}{4L}=Q2.35\times 10^{22}L^{-1}(1000Lm^{-3})\]
\[\left ( \dfrac{N}{V}\right )=Q2.35\times 10^{25}m^{3}\]
The mean free path is
\[\lambda =\dfrac{1}{\sqrt{2}\pi d^{2}(\dfrac{N}{V})}\]
\[\lambda =\dfrac{1}{\sqrt{2}\pi(3.55\times 10^{-10}m)^{2}(Q2.35\times 10^{25}m^{-3})}=7.60\times 10^{-8}m\]
Q2.74a
If a sealed container has of xenon molecules traveling at a speed of 24.6 m/s at 108 °C. How many moles of xenon gas do we have in the container?
S2.74a
\(\bar{E}_{trans}=\dfrac{1}{2}mv^2=\dfrac{3}{2}k_BT\\ m=\dfrac{3k_BT}{v^2}=\dfrac{3(1.381\times 10^{-23}J/K)(381.15K)}{(24.6m/s)^2}*\dfrac{1kg*m^2/s^2}{1J}=Q2.609\times 10^{-23}kg\\ n=\dfrac{m}{molarmass}=Q2.609\times 10^{-23}kg*\dfrac{1000g}{1kg}*\dfrac{mol}{131.3g}=1.987\times 10^{-22}mol\)
Q2.74b
At room temperature (25oC) there are two flasks A and B containing gaseous Oxygen and Hydrogen, respectively, at their equilibrium states. Assuming there is no exchange of heat or work between the systems inside the flasks and the surroundings. Compare the initial velocities between an Oxygen and a Hydrogen molecule in each flask.
Q2.76a
In a insulated container of volume 2.50 L filled with nitrogen gas, the Z1 value is 6.75e19 collisions/second. The temperature measured is 55ºC. Assuming that the collision diameter of N2 is 3.75 Å,
- how many moles of nitrogen gas are present the container?
- find the Z11 value of the gas.
- How does the number of moles affect Z1 and Z11 values of the gas?
Hint: look at collision frequency
S2.76a
a) \[ Z_{1} = \sqrt{2} \pi d^{2} \bar{c} (\dfrac{N}{V}) \]
\[ \Rightarrow N = \dfrac{VZ_{1}}{\sqrt2 \pi d^{2} \bar{c}}\]
\[ \bar{c} = \sqrt{\dfrac{8RT}{\pi M}} = \sqrt{\dfrac{8(8.314 \dfrac{J}{mol \cdot K})(55+273)K}{\pi \cdot 0.014kg})} = 704.3 m/s \]
\[ N = \dfrac{(2.50 L)(\dfrac{1m^{3}}{1000L}) (6.75 \times 10^{19} collision/s)}{\sqrt{2} \pi (3.75 \times 10^{-10}m)^{2} (704.3 m/s)} = 1.017 \times 10^{23} molecules\]
\[ n = \dfrac{N}{N_A} = \dfrac{1.017 \times 10^{23} molecules}{6.022 \times 10^{23} \dfrac{molecules}{mole}} = {\color{red} 0.169 mole N_{2}} \]
b) \[ Z_{11} = \dfrac{1}{2} Z_{1} (\dfrac{N}{V}) \]
\[ Z_{11} = \dfrac{1}{2} (6.75 \times 10^{19}) \dfrac{1.017 \times 10^{23} molecules}{2.50L \times \dfrac{1m^{3}}{1000 L}} = {\color{red} 1.37 \times 10^{45} \dfrac{collisions}{m^{3} \cdot s}} \]
c) Since N = nNA and Z1 is proportional to N, therefore
\[{\color{red} Z_{1} \propto n}\]
similarly, Z11 is proportional to N2, therefore:
\[{\color{red} Z_{11} \propto n^{2}} \]
Q2.76b
For molecular oxygen at \(56^{o}C\), calculate the number of collisions a single molecule makes in 1 second and the total number of binary collisions at P=1.0 atm and P=0.25 atm. How does pressure relate to these two quantities? The collision diameter of oxygen is 3.02 A.
S2.76b
Step 1: (Hint: Calculate the density and average molecular speed)
At P=1.0atm
$$\dfrac{N}{V}=\dfrac{PN_A}{RT}=\dfrac{(1.0atm)(6.022\times 10^{23}mol^{-1})}{0.08206\,L\,atm\,K^{-1}mol^{-1})(273+56)}=Q2.23\times 10^{22}L^{-1}(\dfrac{1000L}{1m^{3}})=2.23\times 10^{22}m^{-3}\]
Step 2:
$$\bar{c}=\sqrt{\dfrac{8RT}{\pi M}}=\sqrt{\dfrac{8(8.3145JK^{-1}mol^{-1})(273+56K)}{\pi (31.998\times 10^{-3}kg\,mol^{-1})}}=466.578ms^{-1}\]
Step 3:
$$z_1=\sqrt{2}\pi d^2\bar{c}\dfrac{N}{V}=\sqrt{2}\pi(3.02\times 10^{-10}m)^{2}(466.578ms^{-1})(2.23\times 10^{22}m^{-3})=4.683\times 10^{28} collisions m^{-3}s^{-1}\]
Step 4:
$$z_{11}=\dfrac{\sqrt{2}}{2}\pi d\bar{c}(\dfrac{N}{V})^{2}=\dfrac{1}{2}(4.2\times 10^{6})(2.23\times 10^{22}m^{-3})=4.683\times 10^{28} collisionsm^{-3}s^{-1}\]
For an ideal gas, \(z_1\) is proportional to P and \(z_{11}\) is proportional to \(P^{2}\). Reducing P to a fourth of its original value (from 1.0 atm to 0.25 atm) will also reduce 2, to one fourth its value at P=1.0atm.
Therefore at P=0.25 atm,
\[z_1=4.2\times 10^{5}collisions\,s^{-1}$$
$$z_{11}=4.683\times 10^{26}\,collisions\,m^{-3}s{-1}\]
Q2.77a
The relationship between the molar mass and root mean square speed of an ideal gas can be described as:
\[\upsilon _{rms}=\sqrt{\frac{3RT}{\mathfrak{M}}}\]
Use this equation to derive Grahm's Law of Effusion:
\[\frac{r_{1}}{r_{2}}=\sqrt{\frac{\mathfrak{M_{2}}}{\mathfrak{M_{1}}}}\]
S2.77a
For two gasses at standard temperature and pressure,
\[\upsilon _{1rms}=\sqrt{\frac{3RT}{\mathfrak{M_{1}}}}\, \, \, \, \, \, \, \, \, \, \, \, \, \, \upsilon _{2rms}=\sqrt{\frac{3RT}{\mathfrak{M_{2}}}}\]
For any of the two gases,
\[\upsilon _{1rms}^{2}=\frac{3RT}{\mathfrak{M_{1}}}\, \, \, \, \, \, \, \, \, \, \, \, \, \, \upsilon _{2rms}^{2}=\frac{3RT}{\mathfrak{M_{2}}}\]
\[R=\frac{\upsilon _{1rms}^{2}\mathfrak{M_{1}}}{3T}=\frac{\upsilon _{2rms}^{2}\mathfrak{M_{2}}}{3T}\]
\[\upsilon _{1rms}^{2}\mathfrak{M_{1}}=\upsilon _{2rms}^{2}\mathfrak{M_{2}}\]
\[\frac{\upsilon _{1rms}^{2}}{\upsilon_{2rms}^{2}}=\frac{\mathfrak{M_{2}}}{\mathfrak{M_{1}}}\]
\[\frac{\upsilon _{1rms}}{\upsilon_{2rms}}=\sqrt{\frac{\mathfrak{M_{2}}}{\mathfrak{M_{1}}}}\]
Which can be rewritten as:
\[\frac{r_{1}}{r_{2}}=\sqrt{\frac{\mathfrak{M_{2}}}{\mathfrak{M_{1}}}}\]
2.9: Graham's Laws of Diffusion and Effusion
Q2.77b
Derive Graham's Law of Effusion (1) from the equation for calculating Kinetic Energy (2).
\[ \begin{align} &\left(1 \right) \ \ \ \frac{v_{1}}{v_{2}}=\sqrt{\frac{m_2}{m_1}} \\ &\left(2 \right) \ \ \ KE =\frac{1}{2}mv^{2}\ \end{align}\]
S2.77b
\[ \begin{align} & \frac{v_{1}}{v_{2}}=\sqrt{\frac{m_2}{m_1}} \ \ KE =\frac{1}{2}mv^{2}\ \\ & KE_1 = KE_2, \ for \ two\ substances \\ & \frac{1}{2}m_1 v_1^{2} = \frac{1}{2}m_2 v_2^{2}, \ multiply \ both \ sides \ by \ two \\ & m_1 v_1^{2} =m_2 v_2^{2} \\ & \frac{v_1^{2}}{v_2^{2}} = \frac{m_2}{m_1}, \ square \ root \ both \ sides \ of \ the \ equation \\ & \underline{ \frac{v_{1}}{v_{2}}=\sqrt{\frac{m_2}{m_1}} } \end{align}\]
Click here and here for more information about effusion and Graham's law.
Q2.78a
How long would it take for oxygen to diffuse in and carbon dioxide to diffuse out of a cell that is 0.1µm2 thick given that the rate of diffusion of carbon dioxide is 0.0016 mm2/s?
S2.78a
\(\dfrac{t_{CO_2}}{t_{O_2}}=\dfrac{r_{O_2}}{r_{CO_2}}=\sqrt{\dfrac{M_{CO_2}}{M_{O_2}}}\\
r_{O_2}=(0.0016mm^2/s)\sqrt{\dfrac{44.01g/mol}{3Q2.0g/mol}}=0.0019mm^2/s\\
t_{CO_2}=0.1\mu m^2*\dfrac{(1mm)^2}{(100\mu m)^2}*\dfrac{s}{0.0016mm^2}=6.25\times 10^{-3}s\\
t_{O_2}=0.1\mu m^2*\dfrac{(1mm)^2}{(100\mu m)^2}*\dfrac{s}{0.0019mm^2}=5.26\times 10^{-3}s\)
Q2.78b
A sample of red gas collected from the emissions of a paper mill effuses through an orifice of unknown size at standard temperature and pressure in 14.1 minutes. Pure diatomic nitrogen gas at standard temperature and pressure effuses through the hole in 11.0 minutes. What is the red gas? How do you know?
S2.78b
mN2 = 28.01 g/mol
tN2/tunk = (munk/mN2)1/2
munk = (tN2/tunk)2 * mN2 = (14.1 min/11.0 min)2 * 28.01 g mol-1
munk = 46.02 g mol-1
The red gas is nitrogen dioxide, a common emission from pulp mills. We know because the diffusion rate corresponds with a molar mass of 46.01g, the molar mass of NO2
Q2.80
An amount of CO2 gas is effused through a small opening at the rate of 0.596 L/min. A homogenous mixture of O2 and N2 in the atmosphere is put under the same conditions for effusion and after 5 minutes, 5.03 L of the mixture was effused. Find the percent composition of the homogenous mixture (molar fraction).
Hint: Look at concept of effusion and its rate
S2.80
\[ \dfrac{r_{CO_{2}}}{r_{mixture}} = \sqrt{\dfrac{M_{mixture}}{M_{CO_{2}}}} \]
\[M_{mixture} = (\dfrac{r_{CO^{2}}}{r_{mixture}})^{2} (M_{CO_{2}}) = (\dfrac{0.596 \dfrac{L}{min}}{\frac{5.03 L}{5 min}})^2 (44.01 \dfrac{g}{mol}) = 15.447 \dfrac{g}{mol}\]
\[ M_{mixture} = M_{N_{2}}X_{N_{2}} + M_{O_{2}}X_{O_{2}} \]
\[ M_{mixture} = M_{N_{2}}X_{N_{2}} + M_{O_{2}}(1-X_{N_{2}}) \]
\[ 15.447 \dfrac{g}{mol} = (14.01 \dfrac{g}{mol})(X_{N_{2}}) + (16.00 \dfrac{g}{mol})(1-X_{N_{2}}) \]
\[ 15.447 = 14.01 X_{N_{2}} + 16.00 - 16.00X_{N_{2}} = -1.99X_{N_{2}} +16.00 \]
\[ X_{N_{2}} = 0.278 \]
\[ X_{O_{2}} = 1-0.278 = 0.722 \]
\[ {\color{red} \% of N_{2} = 27.8\%} \]
\[ {\color{red} \% of O_{2} = 72.2\%} \]
Q2.81a
You are trying to isolate gaseous Nitrogen-14 via effusion in a 50:50 mixture of Nitrogen-14 and Nitrogen-15 respectively. What will be the percentage of enrichment of the mixture after a single stage of separation?
S2.81a
Use Graham's Law of Diffusion and Effusion to solve this problem.
\[ \begin{align} & \frac{r_1}{r_2} = \sqrt{\frac{M_{2}}{M_{1}}} \\ & \frac{ rate \ of \ ^{14}\textrm{N} }{ rate \ of \ ^{15}\textrm{N} } = \sqrt{ \frac{^{15}\textrm{N}}{^{14}\textrm{N}} } \end{align}\]
\[ \begin{align} & \frac{rate \ of \ {}^{14}\textrm{N}}{rate \ of \ {}^{15}\textrm{N}} = \sqrt{\frac{15.0001 \ g \ mol^{-1}}{14.00307 \ g \ mol^{-1}}} \\ & \frac{rate \ of \ {}^{14}\textrm{N}}{rate \ of \ {}^{15}\textrm{N}} = 1.035 \end{align}\]
Since the ratio of rates of effusion is 1.035, in a single step of separation 3.5% more nitrogen-14 will effuse out of the mixture than nitrogen-15. Thus the percent of enrichment would be 3.5% since there is 3.5% more of N-14 now.
Click here and bhere for more information about effusion and Graham's law.
Q2.81b
A mixture of Neon and Helium gas is effused at standard temperature and pressure. Assuming the mixture is equimolar, what is the composition of the gas mixture after effusion?
S2.81b
For the effusion of a binary gas mixture, we can use Graham's Law:
\[\frac{r_{1}}{r_{2}}=\sqrt{\frac{\mathfrak{M_{2}}}{\mathfrak{M_{1}}}}\]
The ratio of the two gasses following effusion given r1 corresponds with neon and r2 corresponds with helium is:
\[\frac{r_{1}}{r_{2}}=\sqrt{\frac{4.003\frac{g}{mol}}{20.180\frac{g}{mol}}}=0.4454\]
Therefore, to calculate the mole fraction of each gas,
\[x_{Ne}=\frac{0.4454}{0.4454+1}=0.3081\]
\[x_{He}=1-x_{Ne}=1-0.3081=0.6919\]
Q2.82
An equimolar mixture of diatomic nitrogen gas and an unknown monatomic gas diffuse through an aperture of unknown size. It is determined that 1.18 times as many moles of the monatomic gas pass through the opening as moles of nitrogen gas. What is the gas?
Q2.82
mN2 = 28.01 g mol-1
nunk/nN2 = (mN2/munk)1/2
munk = mN2/(nunk/nN2)2 = 28.01 g mol-1/(1.18)2 = 20.11 g mol-1
The gas is monatomic and has a mass of roughly 20.11 g/mol, so Neon is the most likely gas.

