25.3: D, L Sugars
- Page ID
- 36455
After completing this section, you should be able to
- identify a specific enantiomer of a monosaccharide as being D or L, given its Fischer projection.
- identify the limitations of the D, L system of nomenclature for carbohydrates.
- assign an R or S configuration to each of the chiral carbon atoms present in a monosaccharide, given its Fischer projection.
- draw the Fischer projection formula for a monosaccharide, given its systematic name, complete with the configuration of each chiral carbon atom.
- construct a molecular model of a monosaccharide, given its systematic name, complete with the configuration of each chiral carbon atom.
Make certain that you can define, and use in context, the key terms below.
- D sugar
- L sugar
If you find that you have forgotten the meanings of terms such as dextrorotatory and polarimeter, refer back to Section 5.3 in which the fundamentals of optical activity were introduced.
How would you set about the task of deciding whether each chiral carbon has an R or an S configuration? True, you could use molecular models, but suppose that a model set had not been available—what would you have done then?
One approach is to focus on the carbon atom of interest and sketch a three-dimensional representation of the configuration around that atom, remembering the convention used in Fischer projections: vertical lines represent bonds going into the page, and horizontal lines represent bonds coming out of the page. Thus, the configuration around carbon atom 2 in structure a can be represented as follows:
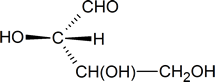
In your mind, you should be able to imagine how this molecule would look if it was rotated so that the bonds that are shown as coming out of the page are now in the plane of the page. [One possible way of doing this is to try and imagine how the molecule would look if it was viewed from a point at the bottom of the page.] What you should see in your mind is a representation similar to the one drawn below.
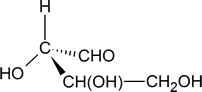
To determine whether the configuration about the central carbon atom is R or S, we must rotate the molecule so that the group with the lowest priority (H), is directed away from the viewer. This effect can be achieved by keeping the hydroxyl group in its present position and moving each of the other three groups one position clockwise.
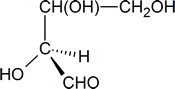
The Cahn-Ingold-Prelog order of priority for the three remaining groups is OH > CHO > CH(OH)CH2OH; thus, we see that we could trace out a counterclockwise path going from the highest-priority group to the second- and third-highest, and we conclude that the central carbon atom has an S configuration.
D and L Labeling of Monosaccharide Stereochemistry
Glyceraldehyde, the simplest possible aldose, is made up of three carbons and only one these is chiral. Glyceraldehyde has two stereoisomers, an R/S pair of enantiomers. Before the R,S system for designating chiral configuration was adopted by organic chemists (R)-glyceraldehyde was called D-glyceraldehyde (Latin for right: dexter) and (S)-glyceraldehdye was called L-glyceraldehyde (Latin for left:laevus). D- and L-glyceraldehyde were then used to provide reference points for designating and drawing all other monosaccharides. Sugars whose Fischer projections have the same configuration at the chiral carbon furthest from the carbonyl group as D-glyceraldehyde are designated as D sugars; those with the same configuration as L-glyceraldehyde are designated as L sugars. D and L designations of sugars are based on the position of the hydroxyl on the chiral carbon farthest from the carbonyl group in the Fischer projection of the molecule. All D-sugars have the –OH on the right side and L-sugars have the –OH on the left side.
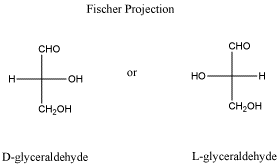
D-sugars predominate in nature, though L-forms of some sugars, such as fucose, do exist. The D and L designation is a bit more complicated than it would appear on the surface. The confusion about D and L arises because the L sugars of a given name (glucose, for example) are mirror images of the D sugars of the same name. This concept is most easily seen with glyceraldehyde. In the same way D- and L- glyceraldehyde represent two enantiomers, the D- and L- forms larger monosaccharides are enantiomers of one another. The figure below shows the structure of D- and L- glucose. Notice that D-glucose is not converted into L-glucose simply by flipping the configuration of the fifth carbon in the molecule. Rather all of the arrangement around all of the chiral centers (horizontal lines) in the Fischer project of D-glucose need to be opposite to make L-glucose.
. 
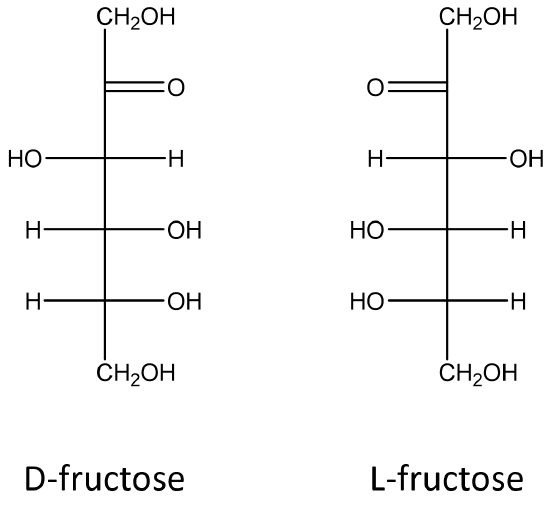
Figure 6. Fischer projections of enantiomers of glucose (left) and fructose (right).
It is important to recognize that the sign of a compound's specific rotation of plane polarized light (+)/(−) does not correlate with its configuration (D or L). The D/L labeling does not indicate which enantiomer is (+)/(−). Rather, it says that the compound's stereochemistry is related to that of the D or L enantiomer of glyceraldehyde. It is a simple matter to measure an optical rotation with a polarimeter. Determining an absolute configuration usually requires chemical interconversion with known compounds by stereospecific reaction paths.
In the following Fischer projections, assign R and S for each chiral center and determine whether each sugar is a D or L sugar.
a)
b)
c)
- Answer
-
a) From top to bottom, 2R, 3R, and it is a D sugar.
b) From top to bottom, 2S, 3R, 4S, and it is an L sugar.
c) From to to bottom, 3R, 4S, and it is an L sugar.

