13.6: ¹H NMR Spectroscopy and Proton Equivalence
- Page ID
- 31539
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to
- identify those protons which are equivalent in a given chemical structure.
- use the 1H NMR spectrum of a simple organic compound to determine the number of equivalent sets of protons present.
Make certain that you can define, and use in context, the key terms below.
- diastereotopic
- enantiotopic
- homotopic
It is important at this stage to be able to identify equivalent protons in any organic compound given the structure of that compound. Once you know the number of different groups of equivalent protons in a compound, you can predict the number (before coupling) and relative strength of signals. Look at the following examples and make sure you understand how the number and intensity ratio of signals are derived from the structure shown.
| Structure | Number of Signals | Ratio of Signals | |
|---|---|---|---|
| \(\ce{\sf{CH3OCH2CH2Br}}\) | 3 | A : B : C | 3 : 2 : 2 |
| 1 | |||
| 3 | A : B : C | 2 : 2 : 6 (or 1 : 1 : 3) | |
| 3 | A : B : C | 2 : 4 : 2 (or 1 : 2 : 1) | |
| 4 | A : B : C : D | 3 : 2 : 2 : 3 | |
| 5 | A : B : C : D : E | 3 : 1 : 1 : 1 : 1 | |
Proton equivalence in proton NMR refers to the concept that not all hydrogen atoms in a molecule produce distinct signals in the NMR spectrum. Instead, chemically equivalent protons, meaning those that occupy identical environments within a molecule, yield the same NMR signal. This concept is essential for interpreting NMR spectra accurately. Chemical equivalence is determined by the molecular structure and symmetry of a molecule. If all protons in all organic molecules had the same resonance frequency in an external magnetic field of a given strength, the information in the previous paragraph would be interesting from a theoretical standpoint, but would not be terribly useful to organic chemists. Fortunately for us, however, resonance frequencies are not uniform for all protons in a molecule. In an external magnetic field of a given strength, protons in different locations in a molecule have different resonance frequencies, because they are in non-identical electronic environments. In methyl acetate, for example, there are two ‘sets’ of protons. The three protons labeled Ha have a different - and easily distinguishable – resonance frequency than the three Hb protons, because the two sets of protons are in non-identical environments: they are, in other words, chemically nonequivalent.

On the other hand, the three Ha protons are all in the same electronic environment, and are chemically equivalent to one another. They have identical resonance frequencies. The same can be said for the three Hb protons. These protons are considered to be homotopic. Homotopic protons are chemically identical, so electronically equivalent, thus show up as identical NMR absorptions.
The ability to recognize chemical equivalency and nonequivalency among atoms in a molecule will be central to understanding NMR. In each of the molecules below, all protons are chemically equivalent, and therefore will have the same resonance frequency in an NMR experiment.
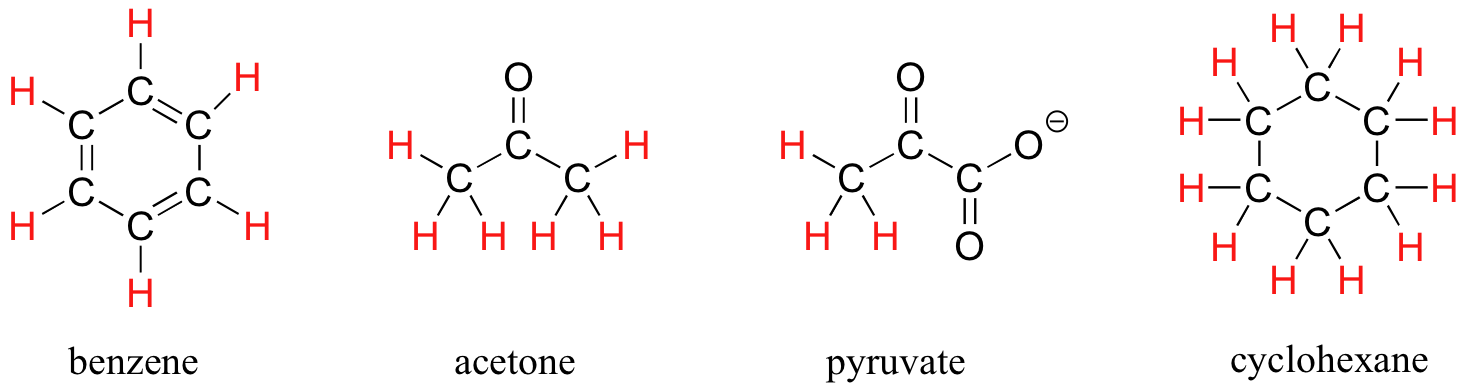
You might expect that the equatorial and axial hydrogens in cyclohexane would be non-equivalent, and would have different resonance frequencies. In fact, an axial hydrogen is in a different electronic environment than an equatorial hydrogen. Remember, though, that the molecule rotates rapidly between its two chair conformations, meaning that any given hydrogen is rapidly moving back and forth between equatorial and axial positions. It turns out that, except at extremely low temperatures, this rotational motion occurs on a time scale that is much faster than the time scale of an NMR experiment.
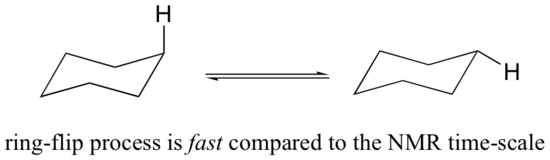
In this sense, NMR is like a camera that takes photographs of a rapidly moving object with a slow shutter speed - the result is a blurred image. In NMR terms, this means that all 12 protons in cyclohexane are equivalent.
Each the molecules in the next figure contains two sets of protons, just like our previous example of methyl acetate, and again in each case the resonance frequency of the Ha protons will be different from that of the Hb protons.
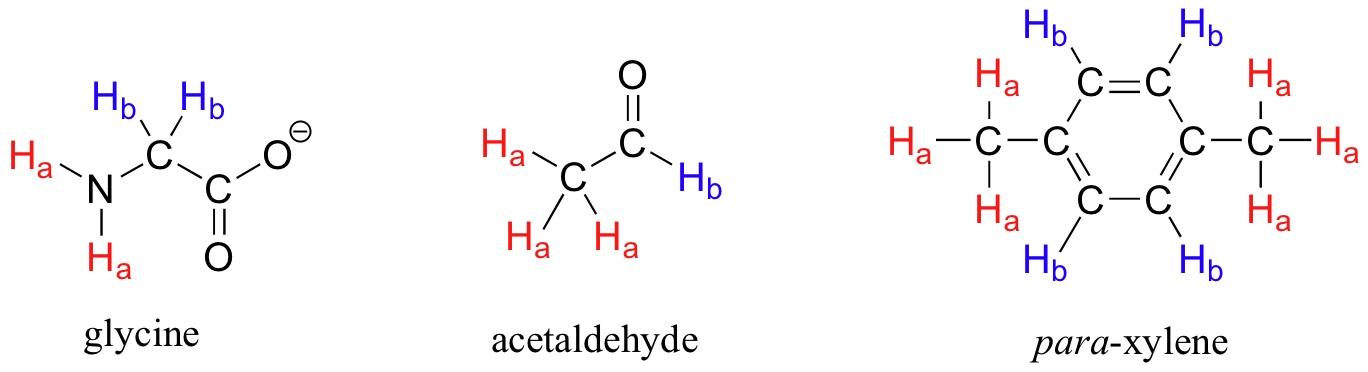
Notice how the symmetry of para-xylene results in there being only two different sets of protons.
Most organic molecules have several sets of protons in different chemical environments, and each set, in theory, will have a different resonance frequency in 1H-NMR spectroscopy.
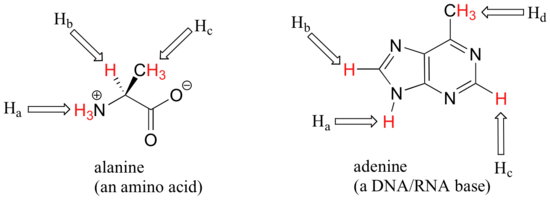
When stereochemistry is taken into account, the issue of equivalence vs nonequivalence in NMR starts to get a little more complicated. It should be fairly intuitive that hydrogens on different sides of asymmetric ring structures and double bonds are in different electronic environments, and thus are non-equivalent and have different resonance frequencies. In the alkene and cyclohexene structures below, for example, Ha is trans to the chlorine substituent, while Hb is cis to chlorine.
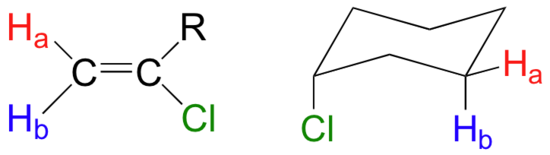
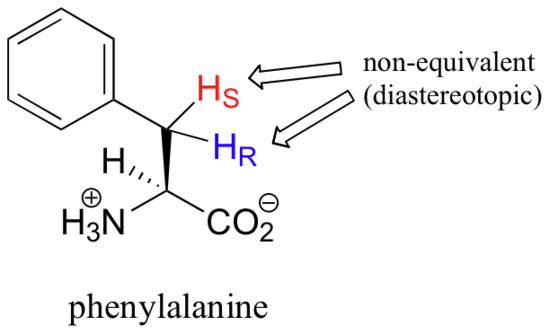
What is not so intuitive is that diastereotopic hydrogens (section 3.10) on chiral molecules are also non-equivalent:
However, enantiotopic and homotopic hydrogens are chemically equivalent. To determine if protons are homotopic or enantiotopic, you can do a thought experiment by replacing one H with X followed by the other H by X. In pyruvate below, if you replace any of the Hs with an X, then you would get the same molecule. These protons are homotopic. In dihydroxyacetone phosphate, this is not quite the case. If you exchange HR for X, then you would create a stereocenter with R configuration. If you exchange HS for X, then you would create a stereocenter with S configuration. The two "new molecules" would have the relationship of being enantiomers. Therefore HR and HS are enantiotopic protons. The only way these protons will show up different under NMR experimental conditions would be if you used a solvent that was chiral. Since most common solvents are all achiral, the enantiotopic protons are NMR equivalent and will show up as if they were the same proton.
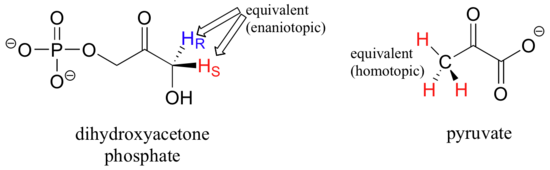
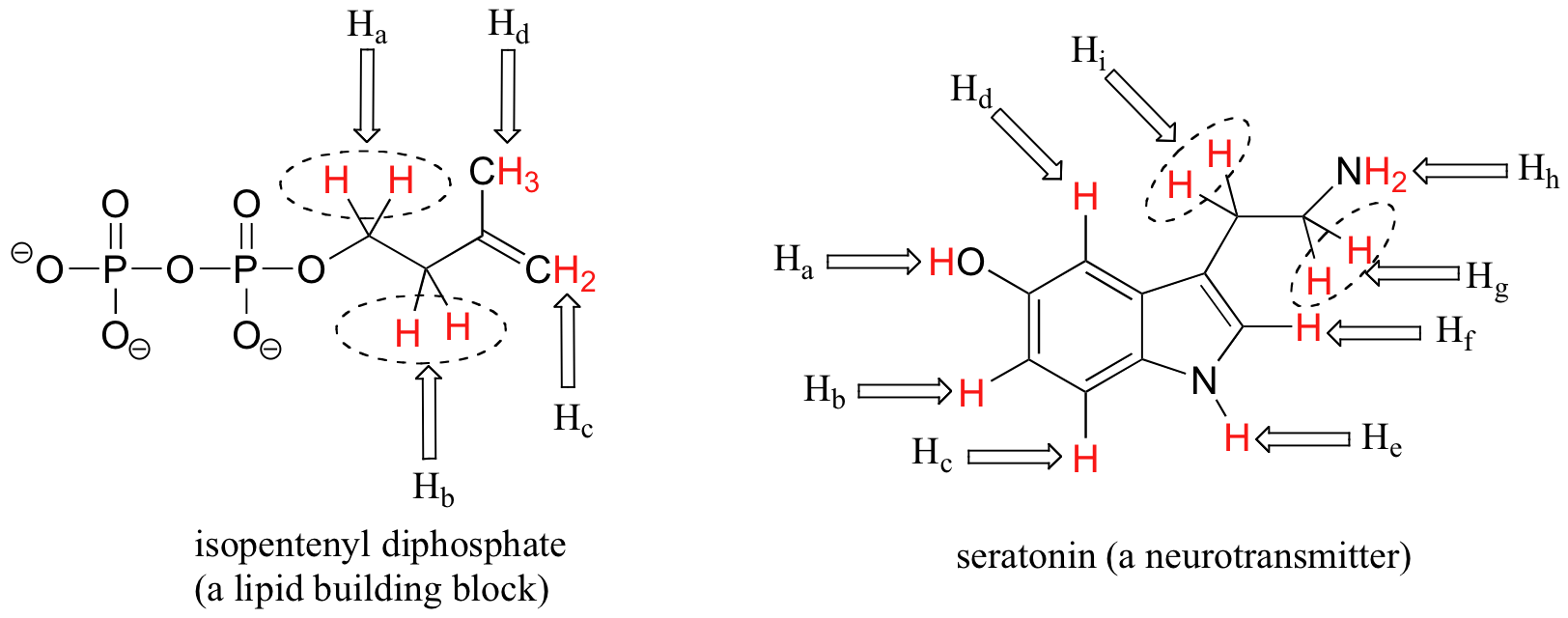
How many different sets of protons do the following molecules contain? (count diastereotopic protons as non-equivalent).
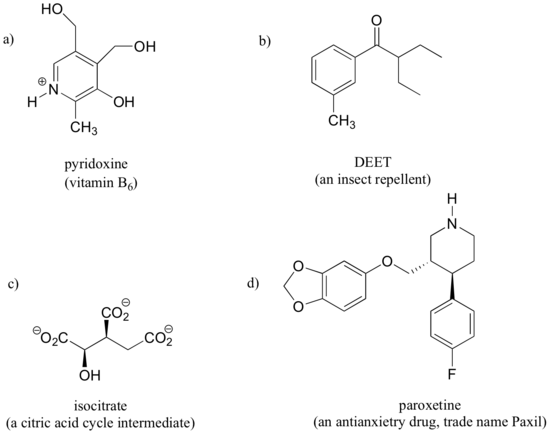
How many non-equivalent hydrogen are in the following molecules; how many different signals will you see in a H1 NMR spectrum.
- CH3CH2CH2Br
- CH3OCH2C(CH3)3
- Ethyl Benzene
- 2-methyl-1-hexene
- Answer
-
A. 3; B. 3; C. 5; D. 7

