Chapter 5 Solutions
- Page ID
- 1120
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In-chapter exercises
E5.1:
a) 8 b) 8 c) 5 d) 18
E5.2:
a) 1 ppm = 300 Hz, so 4.56 ppm corresponds to 1368 Hz on the 300 MHz instrument. On the 200 MHz instrument, the chemical shift is 912 Hz.
b) 300 MHz instrument: 300,001,368 Hz. 200 MHz instrument: 200,000,912 Hz.
E5.3: the acetone:dichloromethane ratio is 0.76:1. If it was a 1:1 ratio, the signal integration ratio would be 3:1 because acetone has 6 protons while dichloromethane has 2. So you need to divide the 2.3 integral value by a factor of 3 to get 0.76.
E5.4:There are three peaks: two from para-xylene and one from acetone. The acetone peak and the para-xylene methyl peak both represent six protons, so the ratio of their integration values is simply 64 to 36 or 1 to 0.56. The ratio of the para-xylene methyl peak to the para-xylene aromatic peak is 6 to 4, or 0.56 to 0.37. So the final integral ratio of acetone:methyl:aromatic signals should be 1 to 0.56 to 0.37.
E5.5:The molecule contains two groups of equivalent protons: the twelve pointing to the outside of the ring, and the six pointing into the center of the ring. The molecule is aromatic, as evidenced by the chemical shift of the ‘outside’ protons’ (and the fact that there are 18 pelectrons, a Hückel number). The inside protons are shielded by the induced field of the aromatic ring current, because inside the ring this field points in the opposite direction of B0. This is the source of the unusually low (negative relative to TMS) chemical shift for these protons.
E5.6:
a)
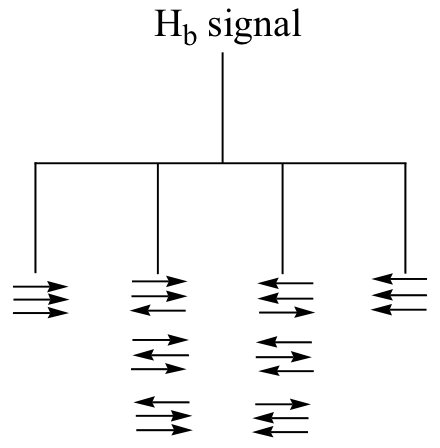
b) The figure above demonstrates that the quartet subpeaks integrate to 1:3:3:1 (eg., there are three ways for two spins to be aligned with B0 and one against B0). As an analogy, if you flip three coins at once, you have a 1 in eight chance of getting all heads, 1 in 8 chance of all tails, a 3 in 8 chance of two heads and a tail, and a 3 in 8 chance of two tails and a head.
E5.7:
Because of the symmetry in the molecule, there are only four proton signals. Predicted splitting is indicated.
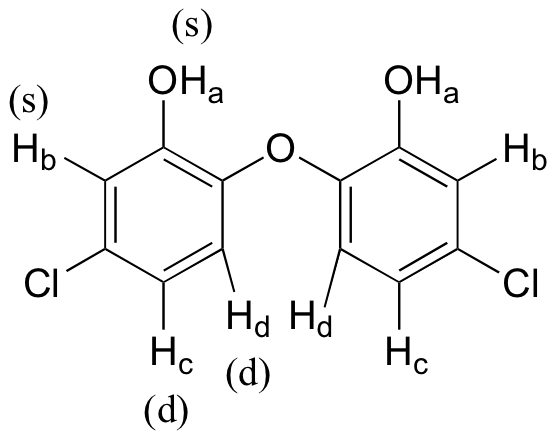
E5.8:
(recall that splitting is generally not seen with protons on heteroatoms)
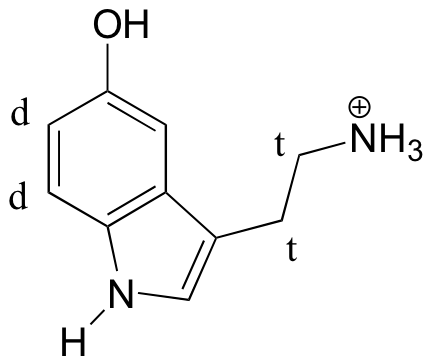
E5.9:
E5.10:We can think of this signal as being a triplet of triplets, but because the two coupling constants are very close, what we would actually see is a 1,2,3,2,1 pentet.

E5.11:
a) 8 signals (each carbon is different)
b) 11 signals (the two enantiotopic CH2CH3 groups are NMR-equivalent)
c) 6 signals (each carbon is different)
d) 16 signals (the fluorobenzene group only contributes 4 signals due to symmetry)
E5.12:
a) 5 signals
b) 5 signals
c) 3 signals
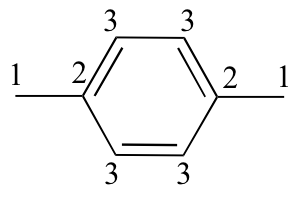
d) 6 signals
E5.13:
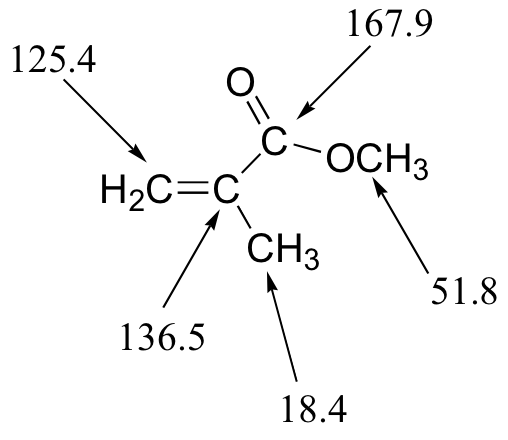
E5.14:
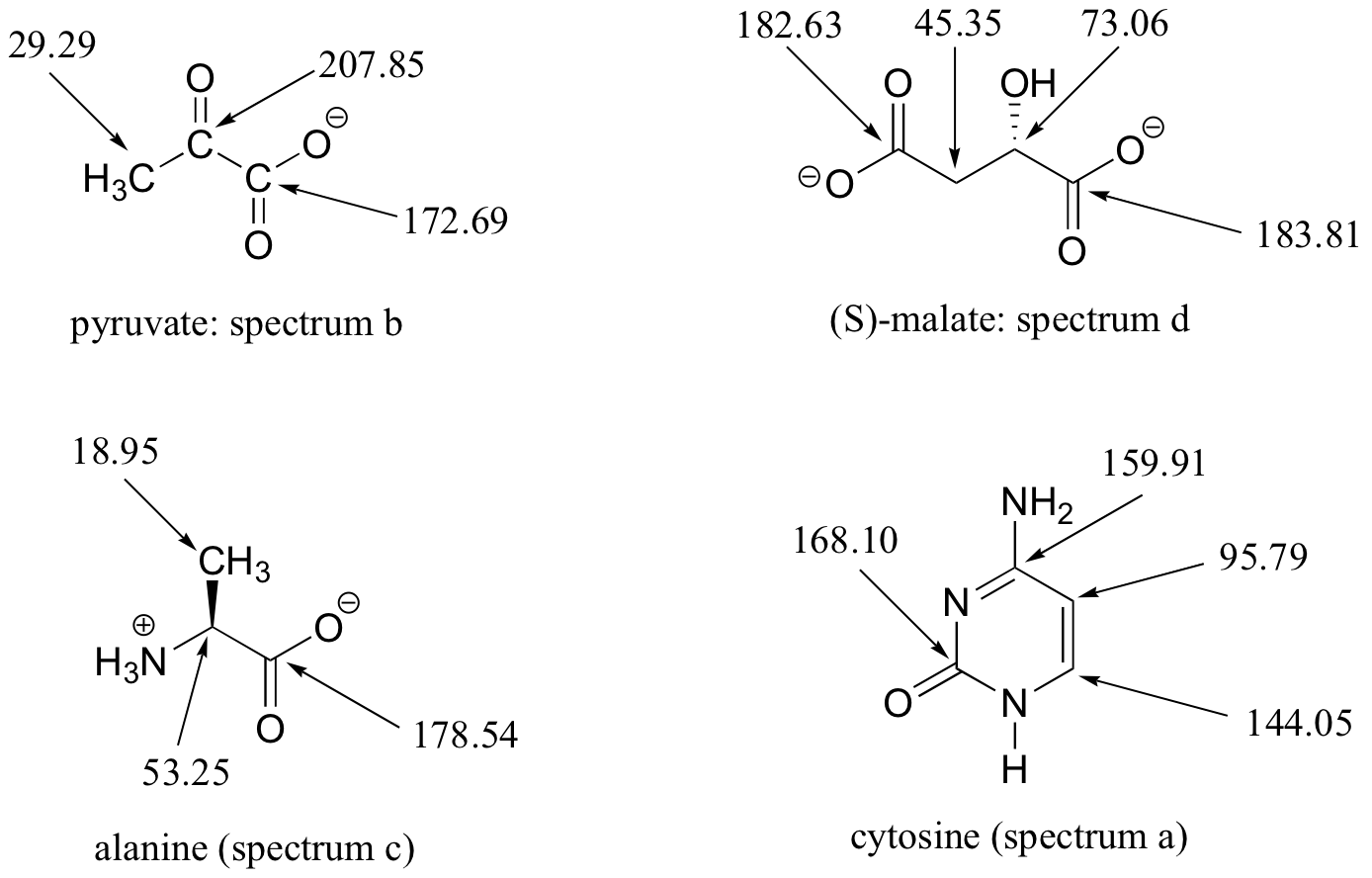
E5.15:
E5.16: This benzylic carbocation is especially stable, as the positive charge is stabilized by two benzene rings.
End-of-chapter problems
P5.1: (structures n and o are chiral, and thus we must consider diastereotopic protons)
| structure | # 1H peaks | # 13C peaks |
| a | 4 | 5 |
| b | 2 | 3 |
| c | 4 | 4 |
| d | 5 | 4 |
| e | 2 | 3 |
| f | 3 | 4 |
| g | 4 | 6 |
| h | 3 | 6 |
| i | 1 | 2 |
| j | 2 | 2 |
| k | 3 | 4 |
| l | 5 | 5 |
| m | 4 | 3 |
| n | 6 | 4 |
| o | 10 | 5 |
P5.2: (valine and leucine both have diastereotopic (and thus nonequivalent) methyl groups.
| Amino acid | # 13C signals |
| glycine | 2 |
| alanine | 3 |
| valine | 5 |
| leucine | 6 |
| isoleucine | 6 |
| phenylalanine | 7 |
| tyrosine | 7 |
| tryptophan | 11 |
| methionine | 5 |
| cysteine | 3 |
| serine | 3 |
| threonine | 4 |
| arginine | 6 |
| lysine | 6 |
| histidine | 6 |
| proline | 5 |
| glutamate | 5 |
| aspartate | 4 |
| glutamine | 5 |
| asparagine | 4 |
P5.3:
a) On a 300 MHz instrument, 1 ppm = 300 Hz, thus a chemical shift of 2.9634 ppm corresponds to 889.0 Hz. The downfield subpeak is 889.0 Hz plus ½ of the coupling constant, or 893.1 Hz. Correspondingly, the upfield subpeak is at 889.0 Hz minus ½ of the coupling constant, or 884.9 Hz.
b) In a 100 MHz instrument, 1 ppm = 100 Hz, so the chemical shift of 2.9634 ppm corresponds to 296.34 Hz. Adding and subtracting ½ of the coupling constant gives us chemical shift values for the two subpeaks of 300.4 Hz and 292.2 Hz.
P5.4: The chemical shift, in Hz, of the overall signal is (1.7562 ppm)(300 Hz/ppm) = 526.9 Hz. The furthest downfield subpeak has a chemical shift of 538.3 Hz (see the figure below). The resonance frequency is this number plus 300 million Hz, or 300,000,538.3 Hz.

P5.5:
A pair of doublets indicates para disubstitution:

P5.6:
Spectrum 1: structure D
Spectrum 2: structure F
Spectrum 3: structure C
Spectrum 4: structure B
Spectrum 5: structure A
Spectrum 6: structure E
P5.7:
Spectrum 7: structure K
Spectrum 8: structure J
Spectrum 9: structure I
Spectrum 10: structure G
Spectrum 11: structure H
Spectrum 12: structure L
P5.8:
Spectrum 13: structure M
Spectrum 14: structure O
Spectrum 15: structure P
Spectrum 16: structure N
Spectrum 17: structure R
Spectrum 18: structure Q
P5.9:
Spectrum 19: structure X
Spectrum 20: structure W
Spectrum 21: structure T
Spectrum 22: structure V
Spectrum 23: structure S
Spectrum 24: structure U
P5.10:
Spectrum 25: structure FF
Spectrum 26: structure BB
Spectrum 27: structure AA
Spectrum 28: structure CC
Spectrum 29: structure EE
Spectrum 30: structure DD
P5.11:
Spectrum 31: structure HH
Spectrum 32: structure KK
Spectrum 33: structure LL
Spectrum 34: structure GG
Spectrum 35: structure JJ
Spectrum 36: structure II
P5.12:
a )
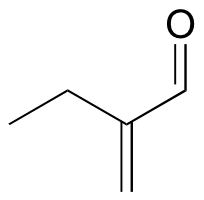
b)

c)
![]()
d)
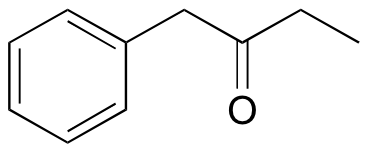
P5.13:
a)
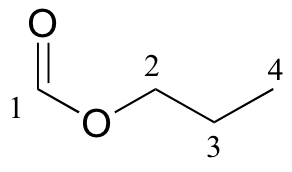
| δ | carbon # |
| 161.12 | 1 |
| 65.54 | 2 |
| 21.98 | 3 |
| 10.31 | 4 |
b)
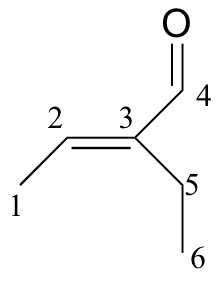
| δ | carbon # |
| 194.72 | 4 |
| 149.10 | 3 |
| 146.33 | 2 |
| 16.93 | 5 |
| 14.47 | 1 |
| 12.93 | 6 |
c)
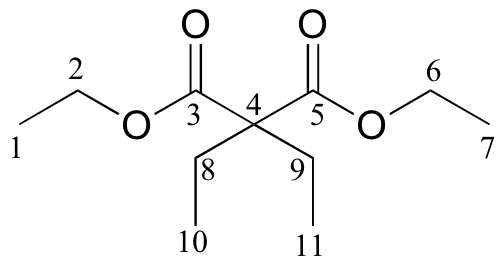
| δ | carbon # |
| 171.76 | 3, 5 |
| 60.87 | 2, 6 |
| 58.36 | 4 |
| 24.66 | 8, 9 |
| 14.14 | 1, 7 |
| 8.35 | 10, 11 |
d)
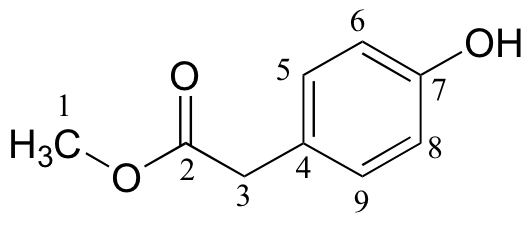
| δ | carbon # |
| 173.45 | 2 |
| 155.01 | 7 |
| 130.34 | 6, 8 |
| 125.34 | 4 |
| 115.56 | 5, 9 |
| 52.27 | 1 |
| 40.27 | 3 |
e)
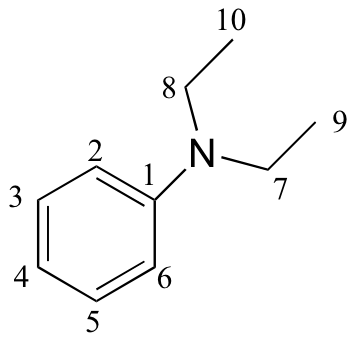
| δ | carbon # |
| 147.79 | 1 |
| 129.18 | 2, 6 |
| 115.36 | 3, 5 |
| 111.89 | 4 |
| 44.29 | 7, 8 |
| 12.57 | 9, 10 |
P5.14: The structure is 3-methyl-2-butanone
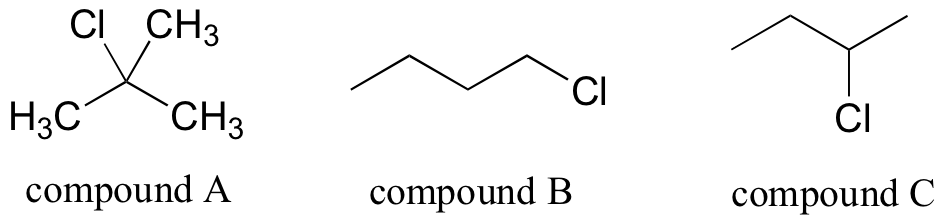
P5.15: First, assign the peaks. 1-bromopropane: Ha is the triplet at 3.4 ppm, Hb is the sextet at 1.9 ppm, Hc is the triplet at 1.0 ppm. 2-bromopropane: Hd is the doublet at 1.7 ppm, He is the septet at 4.3 ppm. Now, just add up the integrations for each molecule and figure the percentage. 1-bromopropane: 0.661 + 0.665 + 1.00 = 2.326. 2-bromopropane: 0.0735 + 0.441 = 0.5145. Percent 2-bromopropane is (0.5145)*100 / (0.5145 + 2.326) = 18.1%.
Notice that even if some peaks overlapped, you could still get this number as long as you could integrate one signal on each molecule: you could, for example, do the same calculation (and get the same result) by comparing integrations of Hc and Hd signals, and just scale based on the fact that the Hc signal represents three protons while the Hd signal represents six protons.

Challenge problems
C5.1: The 13C-NMR signal for the CDCl3 solvent appears as a 1:1:1 triplet due to 1-bond coupling with the deuterium. Protons and 13C nuclei both have a spin quantum number I = ½, which means that they can assume two spin energy levels (+ ½ and – ½ ) when placed in a strong external magnetic field. Deuterium, however, has a spin number I = 1, meaning that it can assume three spin energy level (-1, 0, +1) in the external field. So while a proton splits the signal from a neighboring nucleus into a doublet, a deuterium splits its neighbor’s signal into three sub-peaks of equal height.
C5.2: See J. Chem. Educ. 2000, 77, 363.
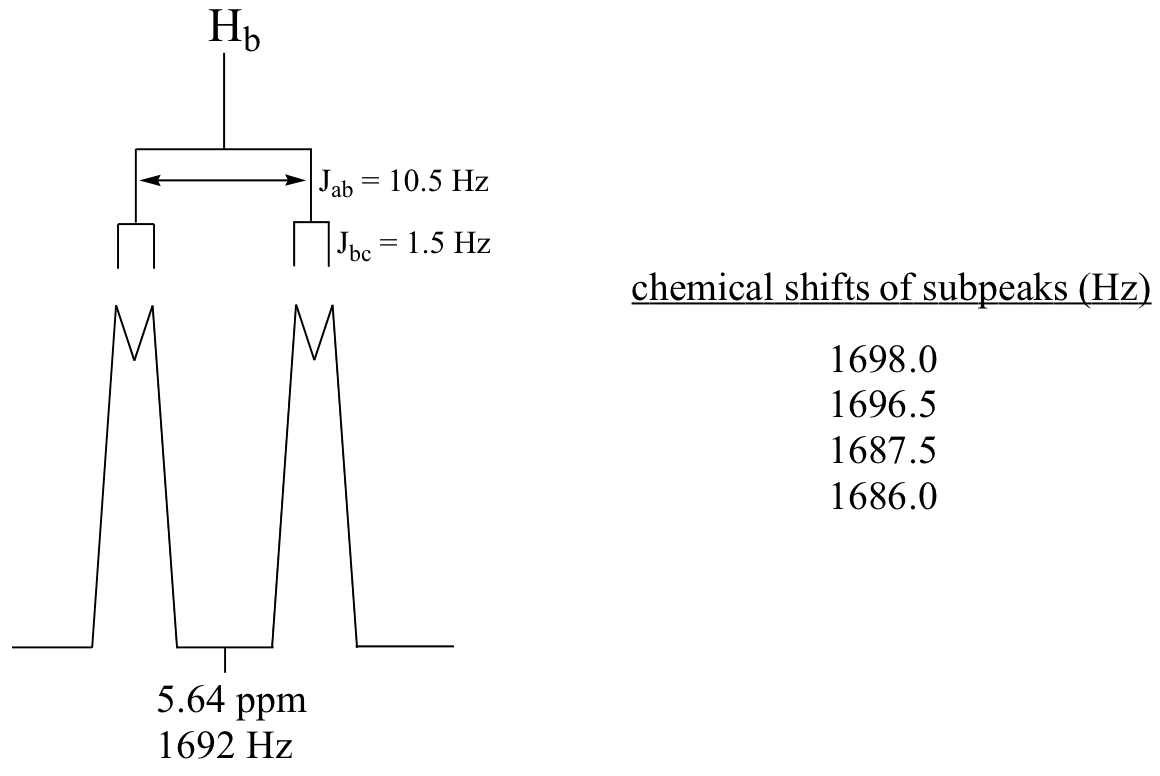
C5.3:First, convert the chemical shift data from ppm to Hz, plot the data, then simply compute the distance between the appropriate sub-peaks. For example, the distance between the two subpeaks in the Ha doublet (9.67 ppm) is about 7.8 Hz, which is the value of Jab. To get Jbc, it would make sense to look at the Hc doublet – except that this signal overlaps with the aromatic signals. Alternatively, we can look at the Hb signal, which is centered at 6.69 ppm. This is a doublet of doublets, but as we already know Jab we can measure Jbc (approximately 16 Hz).
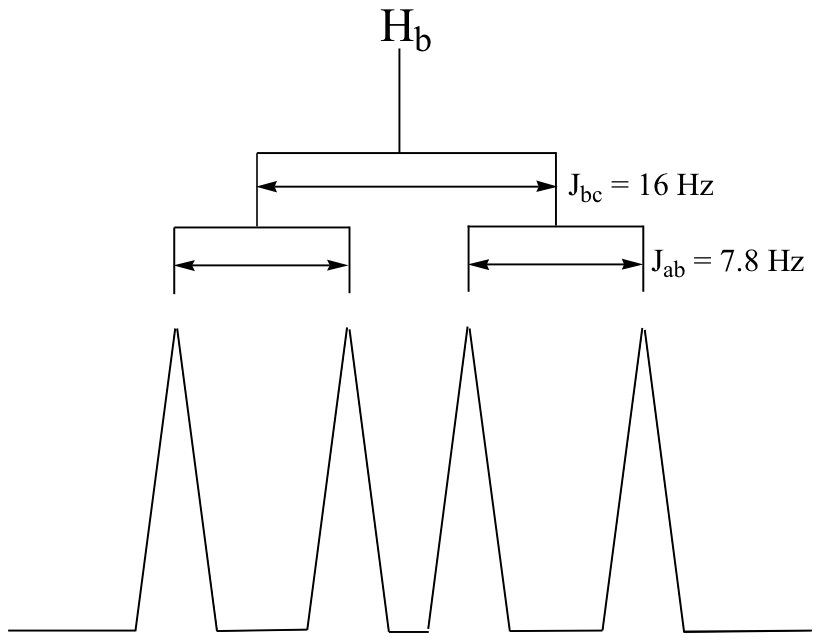
Contributors
- Organic Chemistry With a Biological Emphasis, Tim Soderberg (University of Minnesota, Morris)


