7.11: The Hammond Postulate
- Page ID
- 31460
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to use the Hammond postulate to explain the formation of the most stable carbocation during the addition of a protic acid, HX, to an alkene.
Make certain that you can define, and use in context, the key term below.
- Hammond postulate
So far in this chapter the following points have been made about the electrophilic addition of HX to a double bond.
- The reaction takes place through a two step mechanism which forms a carbocation intermediate.
- During electrophilic addition the carbocation intermediate, and the subsequent H-X bond, forms on the double bond carbon with the most alkyl stubstituents (Markovnikov's rule)
- Carbocations become more stable as the number of alkyl substituents increases.
It appears that the stability of the carbocation reactive intermediate has a direct effect on the products of a reaction. However, it is the activation energy required to reach the transition state of the reaction's rate determine step which determines which determines which product is produced. This implies that there is a relationship between the transition state and the carbocation reactive intermediate in the mechanism of electrophilic addition.
The Hammond Postulate
Chemists are often very interested in the structures of the transition states in a reaction's mechanism. In particular, the transition state for a mechanism's rate determining step directly determines the energy of activation barrier and thereby the rate for the overall reaction. Understanding the structure of a transition state allows chemists to consider structural features which might stabilize or destabilize the transition state causing a corresponding change in the rate of reaction. However, transition state structures cannot be directly observed because they are highly unstable activated complexes which instantly convert to a more stable species. In order to gain some insight into the structure of particular transition state, chemists often invoke the Hammond postulate, which states that a transition state resembles the structure of the nearest stable species (reactant, intermediate or product).
For an exergonic reaction, the transition state is closer in energy to the reactants. Therefore, the structure of the transition state can assumed to resemble the reactants more than the products. Shown below is a hypothetical exergonic reaction between reactant compounds A and B to form the product AB. The Hammond postulate would theorize that the distance between A and B in the transition state would be relatively large thus resembling the reactants where A and B are two isolated species.

For an endergonic reaction, the transition state is closer in energy to the product. Therefore, the structure of the transition state can assumed to resemble the products more than the reactants. In the hypothetical endergonic reaction shown below, reactant compounds C and D react to form the product CD. The Hammond postulate would predict that the distance between C and D in the transition state would be relatively small thus resembling the products where C and D are bonded together as a single product CD.

The Hammond Postulate and Electrophilic Addition
By applying the Hammond postulate and other ideas cultivated in this chapter the reason why electrophilic additions tend to follow Markovnikov's rule. When the energy diagram of an electrophilic addition was discussed in Section 7.2, it was noted the first step of the mechanism was the rate determining step. The first step of the mechanism also is endergonic and results in the formation of a carbocation intermediate.
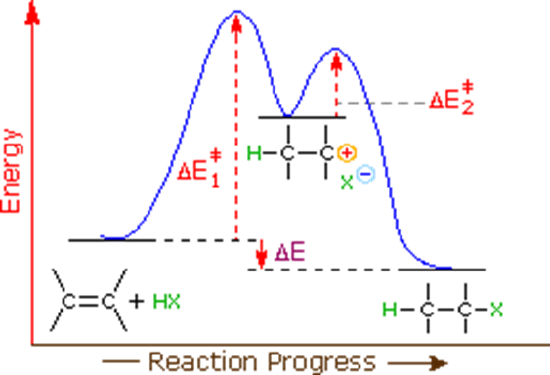
The Hammond postulate suggests that the transition state structure for the first step of the mechanism resembles that of the carbocation intermediate because they are the closest in energy. A transitions state, seen below, is typically drawn as a theoretical structure part way between the reactants and the product. For this transition state the pi bonds and the H-Br bond are in the process of being broken and are represented with a dashed line. The C-H bond is in the process of being formed so it also represented with a dashed line. The bromine is shown with a partial negative charge (sigma-) because it is becoming a bromide ion (Br-) which has a full negative charge. Most importantly, the carbon is in the process of becoming a carbocation so it is shown to have a partial positive change (sigma+).
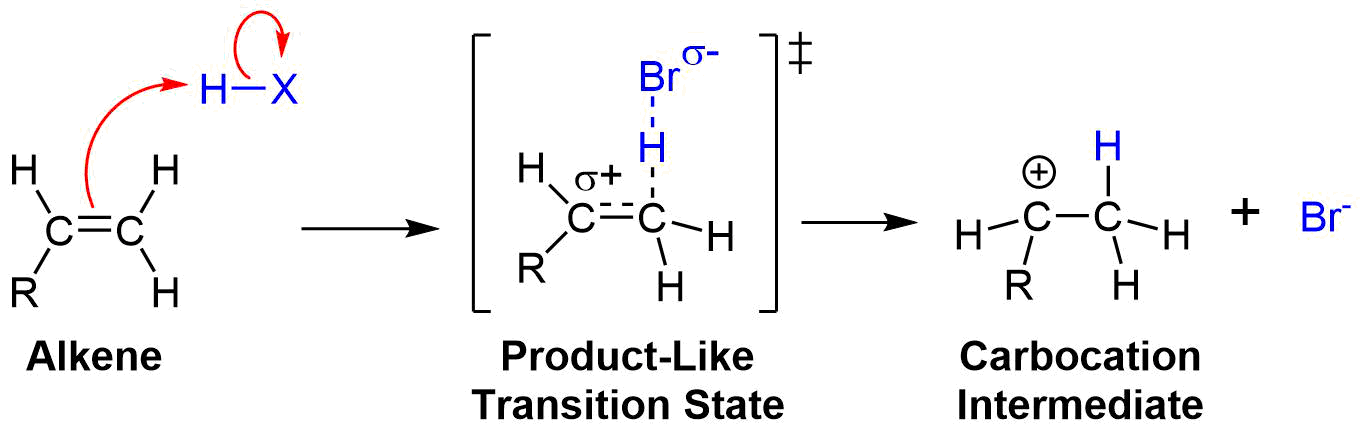
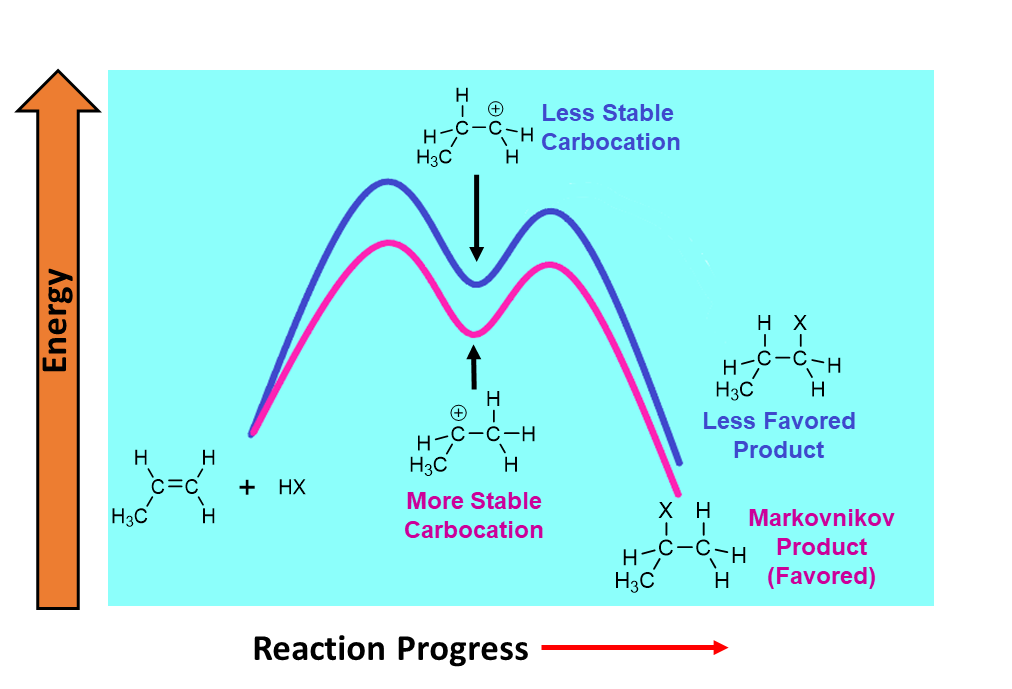
Because the Hammond postulate predicts this transitions state closely resembles the carbocation intermediate, the partial positive charge can said to closely resemble the full positive charge of the carbocation. Consequently, any structural feature that stabilized the carbocation intermediate will also stabilize the transition state. The partial positive charge of the transition state is stabilized by adjacent alkyl groups thorough inductive effects and hyperconjugation much like the carbocation intermediate. Adding more alkyl substituents to the partially positive charged carbon stabilizes the transition state, causing it to become lower in energy. This in turn, decreases the energy of activation and increases the rate of the reaction. In short, during an electrophilic addition, the double bond carbon with the most alkyl substituents will for a carbocation intermediate and therefore its C-X bond faster than the double bond carbon with fewer alkyl substituents. These effects cause electrophillic additions to follow Markovnikov's rule and place the halogen (X) group on the more substituted carbon of asymmetrically alkyl substituted double bond.
| Carbocation Stability |
<< |
<</td> |
≈ |
<</td> |
≈ |
Consider the second step in the electrophilic addition of HBr to an alkene. Is this step exergonic or endergonic and does the transition state represent the product or the reactant (cation)? Draw out an energy diagram of this step reaction.
- Answer
-
Exergonic and the transition state (second step) represents the reactant (cation). As shown to go from intermediate cation to final product the step is exergonic.
Consider the second step in the electrophilic addition of HBr to an alkene. Is this step exergonic or endergonic and does the transition state represent the product or the reactant (cation)? Draw out an energy diagram of this step reaction.
- Answer
-
Exergonic and the transition state (second step) represents the reactant (cation). As shown to go from intermediate cation to final product the step is exergonic.

