6.10: Describing a Reaction - Intermediates
- Page ID
- 31445
After completing this section, you should be able to
- explain the difference between a transition state and an intermediate.
- draw a reaction energy diagram for a given multistep process.
- interpret the reaction energy diagram of a multistep process (e.g., determine which of the steps is rate-determining).
Make certain that you can define, and use in context, the key term below.
- reaction intermediate
Each step in a multistep reaction has its own activation energy. The overall activation energy is the difference in energy between the reactants and the transition state of the slowest (rate-determining) step. The rate-determining step, that is, the one that controls the overall rate of reaction, is the step with the highest activation energy.
A second model for a nucleophilic substitution reaction is called the 'dissociative', or 'SN1' mechanism: in this picture, the C-X bond breaks first, before the nucleophile approaches:
This results in the formation of a carbocation: because the central carbon has only three bonds, it bears a formal charge of +1. Recall that a carbocation should be pictured as sp2 hybridized, with trigonal planar geometry. Perpendicular to the plane formed by the three sp2 hybrid orbitals is an empty, unhybridized p orbital.
In the second step of this two-step reaction, the nucleophile attacks the empty, 'electron hungry' p orbital of the carbocation to form a new bond and return the carbon to tetrahedral geometry.
We saw that SN2 reactions result specifically in inversion of stereochemistry at the electrophilic carbon center. What about the stereochemical outcome of SN1 reactions? In the model SN1 reaction shown above, the leaving group dissociates completely from the vicinity of the reaction before the nucleophile begins its attack. Because the leaving group is no longer in the picture, the nucleophile is free to attack from either side of the planar, sp2-hybridized carbocation electrophile. This means that about half the time the product has the same stereochemical configuration as the starting material (retention of configuration), and about half the time the stereochemistry has been inverted. In other words, racemization has occurred at the carbon center. As an example, the tertiary alkyl bromide below would be expected to form a racemic mix of R and S alcohols after an SN1 reaction with water as the incoming nucleophile.
Draw the structure of the intermediate in the two-step nucleophilic substitution reaction above.
- Answer
-
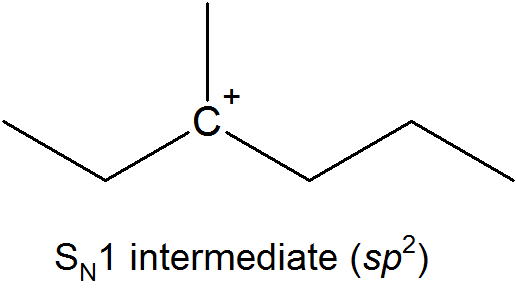
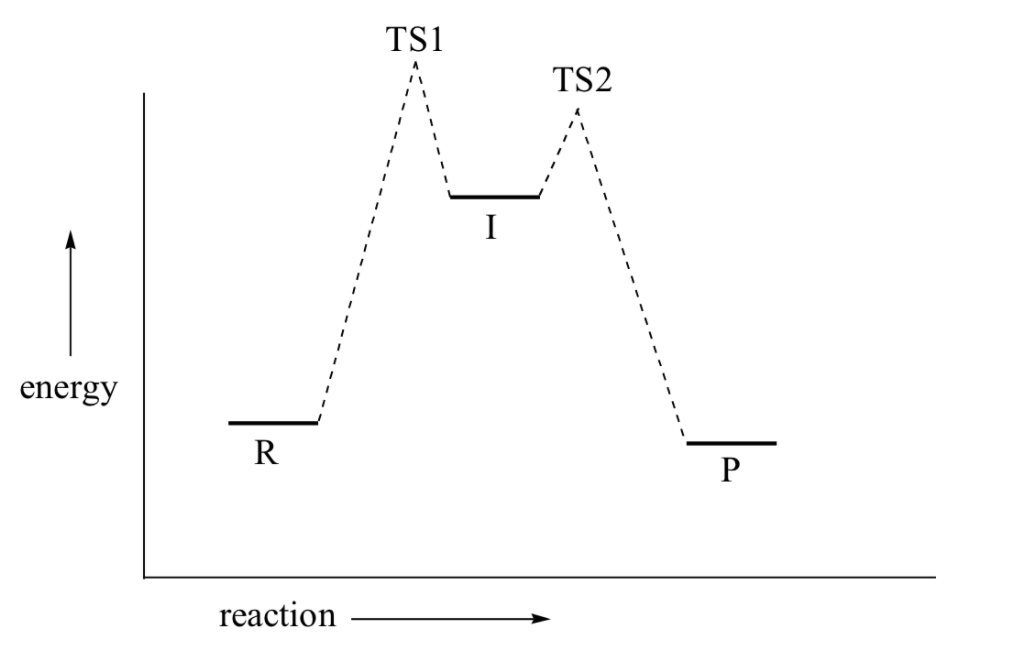
The SN1 reaction we see an example of a reaction intermediate, a very important concept in the study of organic reaction mechanisms that was introduced earlier in the module on organic reactivity Recall that many important organic reactions do not occur in a single step; rather, they are the sum of two or more discreet bond-forming / bond-breaking steps, and involve transient intermediate species that go on to react very quickly. In the SN1 reaction, the carbocation species is a reaction intermediate. A potential energy diagram for an SN1 reaction shows that the carbocation intermediate can be visualized as a kind of valley in the path of the reaction, higher in energy than both the reactant and product but lower in energy than the two transition states.
Draw structures representing TS1 and TS2 in the reaction above. Use the solid/dash wedge convention to show three dimensions.
- Answer
-
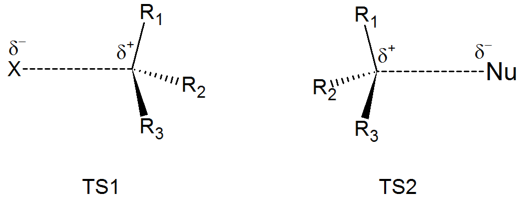
Recall that the first step of the reaction above, in which two charged species are formed from a neutral molecule, is much the slower of the two steps, and is therefore rate-determining. This is illustrated by the energy diagram, where the activation energy for the first step is higher than that for the second step. Also recall that an SN1 reaction has first order kinetics, because the rate determining step involves one molecule splitting apart, not two molecules colliding
We come now to the subject of catalysis. Our hypothetical bowl of sugar (from section 6.2) is still stubbornly refusing to turn into carbon dioxide and water, even though by doing so it would reach a much more stable energy state. There are, in fact, two ways that we could speed up the process so as to avoid waiting several millennia for the reaction to reach completion. We could supply enough energy, in the form of heat from a flame, to push some of the sugar molecules over the high energy hill. Heat would be released from the resulting exothermic reaction, and this energy would push more molecules over their energy hills, and so on - the sugar would literally burn up.
A second way to make the reaction go faster is to employ a catalyst. You probably already know that a catalyst is an agent that causes a chemical reaction to go faster by lowering its activation energy.
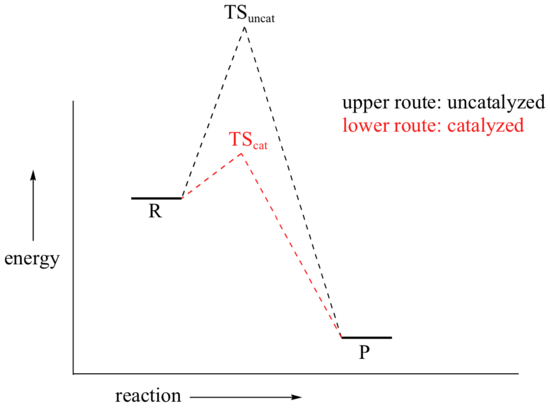
How might you catalyze the conversion of sugar to carbon dioxide and water? It’s not too hard – just eat the sugar, and let your digestive enzymes go to work catalyzing the many biochemical reactions involved in breaking it down. Enzymes are proteins, and are very effective catalysts. ‘Very effective’ in this context means very specific, and very fast. Most enzymes are very selective with respect to reactant molecules: they have evolved over millions of years to catalyze their specific reactions. An enzyme that attaches a phosphate group to glucose, for example, will not do anything at all to fructose (the details of these reactions are discussed in section 10.2B).
Glucose kinase is able to find and recognize glucose out of all of the other molecules floating around in the 'chemical soup' of a cell. A different enzyme, fructokinase, specifically catalyzes the phosphorylation of fructose.
We have already learned (section 3.9) that enzymes are very specific in terms of the stereochemistry of the reactions that they catalyze . Enzymes are also highly regiospecific, acting at only one specific part of a molecule. Notice that in the glucose kinase reaction above only one of the alcohol groups is phosphorylated.
Finally, enzymes are capable of truly amazing rate acceleration. Typical enzymes will speed up a reaction by anywhere from a million to a billion times, and the most efficient enzyme currently known to scientists is believed to accelerate its reaction by a factor of about 1017 (see Chemical and Engineering News, March 13, 2000, p. 42 for an interesting discussion about this enzyme, orotidine monophosphate decarboxylase).
We will now begin an exploration of some of the basic ideas about how enzymes accomplish these amazing feats of catalysis, and these ideas will be revisited often throughout the rest of the text as we consider various examples of enzyme-catalyzed organic reactions. But in order to begin to understand how enzymes work, we will first need to learn (or review, as the case may be) a little bit about protein structure.
Draw an energy diagram with a exergonic first step and an endergonic second step. Label the diagram.
- Answer
-

