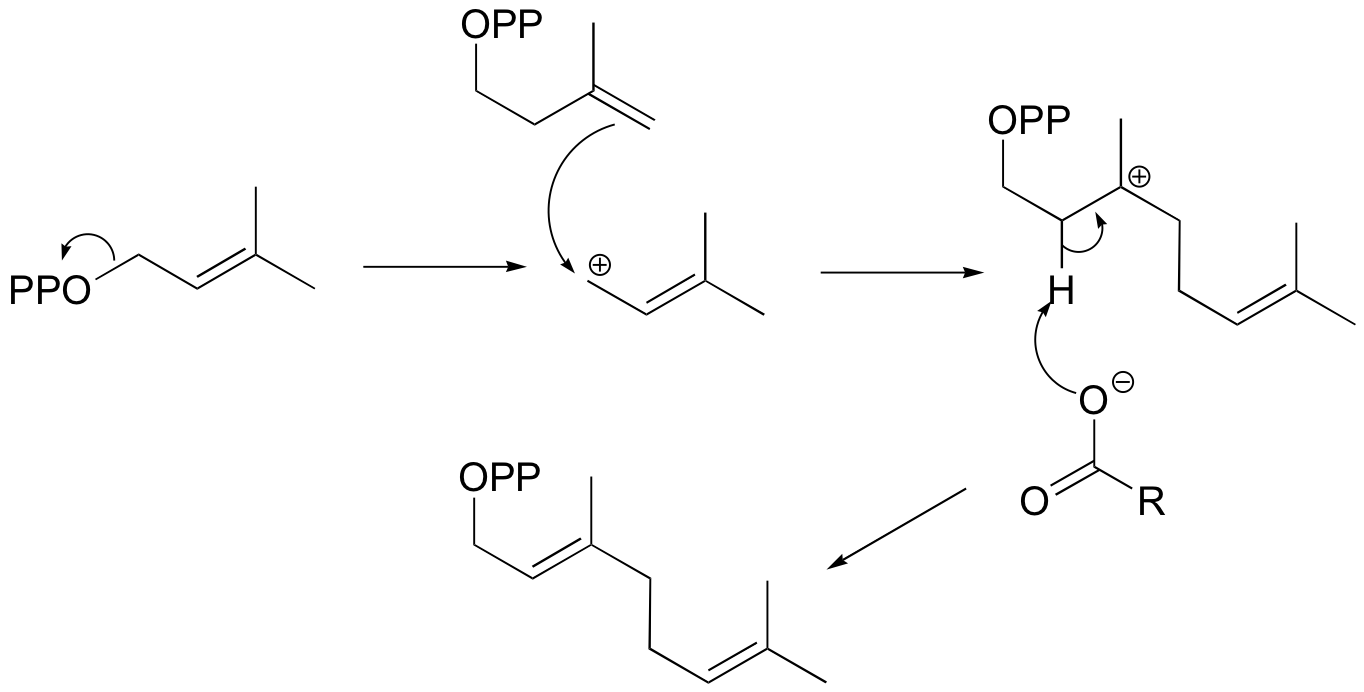
6.2: Energy diagrams
- Page ID
- 1067
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You may recall from general chemistry that it is often convenient to describe chemical reactions with energy diagrams. In an energy diagram, the vertical axis represents the overall energy of the reactants, while the horizontal axis is the ‘reaction coordinate’, tracing from left to right the progress of the reaction from starting compounds to final products. The energy diagram for a typical SN2 reaction might look like this:
Despite its apparent simplicity, this energy diagram conveys some very important ideas about the thermodynamics and kinetics of the reaction. Recall that when we talk about the thermodynamics of a reaction, we are concerned with the difference in energy between reactants and products, and whether a reaction is ‘downhill’ (exergonic, energy releasing) or ‘uphill (endergonic, energy absorbing). When we talk about kinetics, on the other hand, we are concerned with the rate of the reaction, regardless of whether it is uphill or downhill thermodynamically.
First, let’s review what this energy diagram tells us about the thermodynamics of the reaction illustrated by the energy diagram above. The energy level of the products is lower than that of the reactants. This tells us that the change in standard Gibbs Free Energy for the reaction (ΔG˚rnx) is negative. In other words, the reaction is exergonic, or ‘downhill’. Recall that the ΔG˚rnx term encapsulates both ΔH˚rnx, the change in enthalpy (heat) and ΔS˚rnx , the change in entropy (disorder):
ΔG˚ = ΔH˚- TΔS˚
where T is the absolute temperature in Kelvin. For chemical processes where the entropy change is small (~0), the enthalpy change is essentially the same as the change in Gibbs Free Energy. Energy diagrams for these processes will often plot the enthalpy (H) instead of Free Energy for simplicity.
The standard Gibbs Free Energy change for a reaction can be related to the reaction's equilibrium constant (Keq) by a simple equation:
ΔG˚ = -RT ln Keq
where:
- Keq = [product] / [reactant] at equilibrium
- R = 8.314 J×K-1×mol-1 or 1.987 cal× K-1×mol-1
- T = temperature in Kelvin (K)
If you do the math, you see that a negative value for ΔG˚rnx (an exergonic reaction) corresponds - as it should by intuition - to Keq being greater than 1, an equilibrium constant which favors product formation.
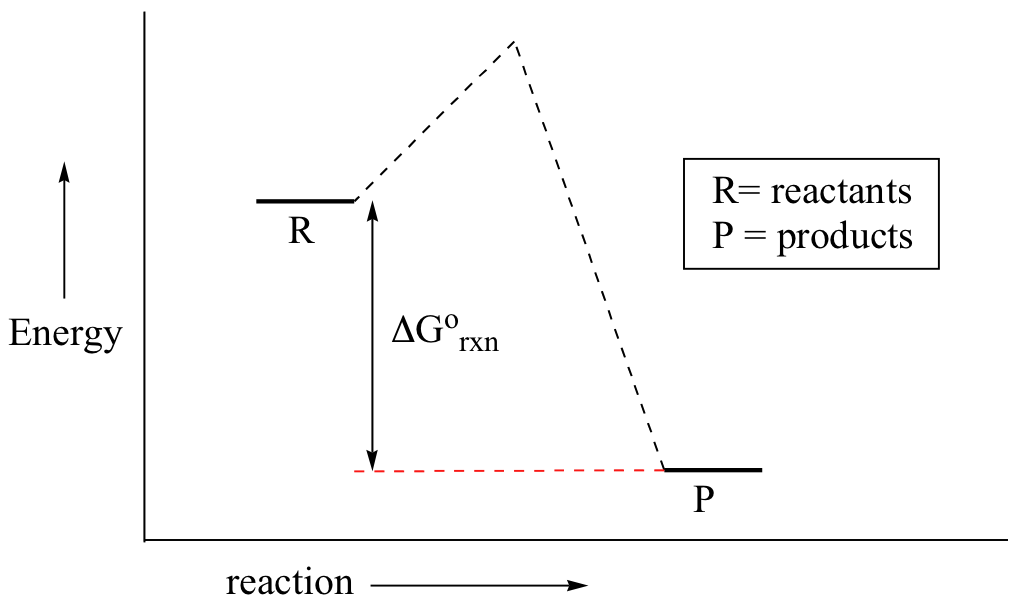
In a hypothetical endergonic (energy-absorbing) reaction the products would have a higher energy than reactants and thus ΔG˚rnx would be positive and Keq would be less than 1, favoring reactants.
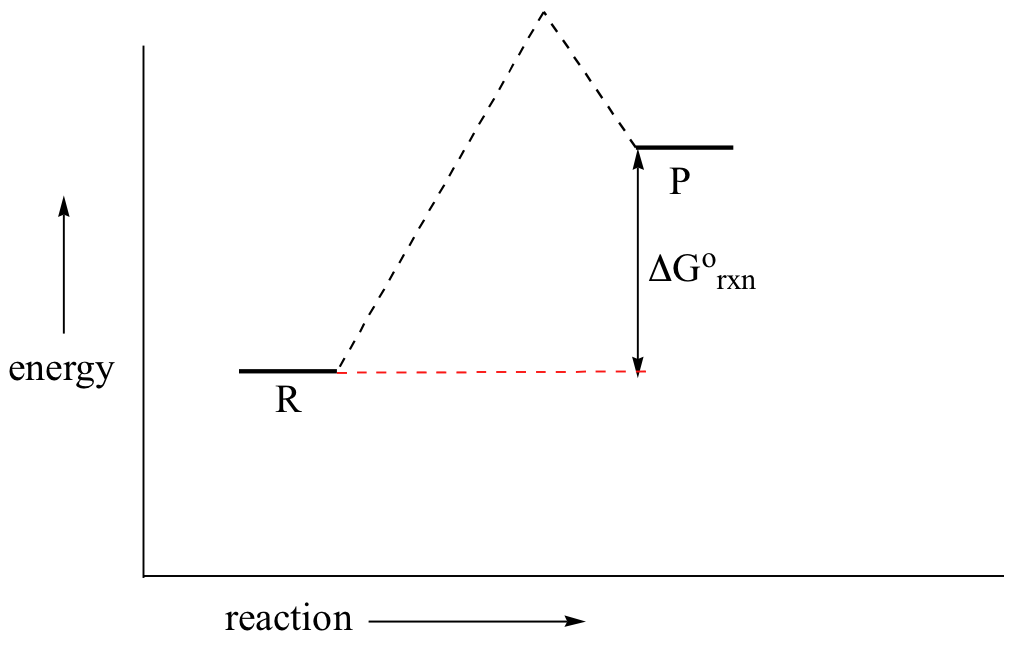
Now, let's move to kinetics. Look again at the energy diagram for exergonic reaction: although it is ‘downhill’ overall, it isn’t a straight downhill run.
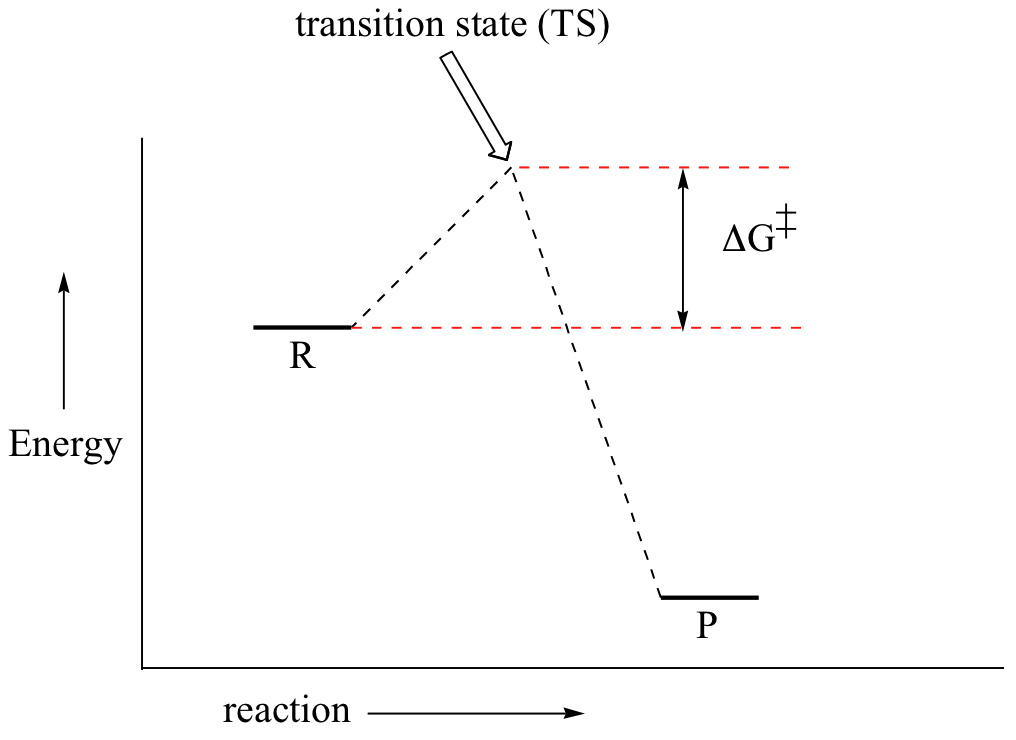
First, an ‘energy barrier’ must be overcome to get to the product side. The height of this energy barrier, you may recall, is called the ‘activation energy’ (ΔG‡). The activation energy is what determines the kinetics of a reaction: the higher the energy hill, the slower the reaction. At the very top of the energy barrier, the reaction is at its transition state (TS), which is the point at which the bonds are in the process of breaking and forming. The transition state is an ‘activated complex’: a transient and dynamic state that, unlike more stable species, does not have any definable lifetime. It may help to imagine a transition state as being analogous to the exact moment that a baseball is struck by a bat. Transition states are drawn with dotted lines representing bonds that are in the process of breaking or forming, and the drawing is often enclosed by brackets. Here is a picture of a likely transition state for our simple SN2 reaction between hydroxide and chloromethane:

The SN2 reaction involves a collision between two molecules: for this reason, we say that it has second order kinetics (this is the source of the number ‘2’ in SN2). The rate expression for this type of reaction is:
rate = k[reactant 1][reactant 2]
. . . which tells us that the rate of the reaction depends on the rate constant k as well as on the concentration of both reactants. The rate constant can be determined experimentally by measuring the rate of the reaction with different starting reactant concentrations. The rate constant depends on the activation energy, of course, but also on temperature: a higher temperature means a higher k and a faster reaction, all else being equal. This should make intuitive sense: when there is more heat energy in the system, more of the reactant molecules are able to get over the energy barrier.
Here is one more interesting and useful expression. Consider a simple reaction where the reactants are A and B, and the product is AB (this is referred to as a condensation reaction, because two molecules are coming together, or condensing). If we know the rate constant k for the forward reaction and the rate constant kreverse for the reverse reaction (where AB splits apart into A and B), we can simply take the quotient to find our equilibrium constant Keq:
![]()
This too should make some intuitive sense; if the forward rate constant is higher than the reverse rate constant, equilibrium should lie towards products.
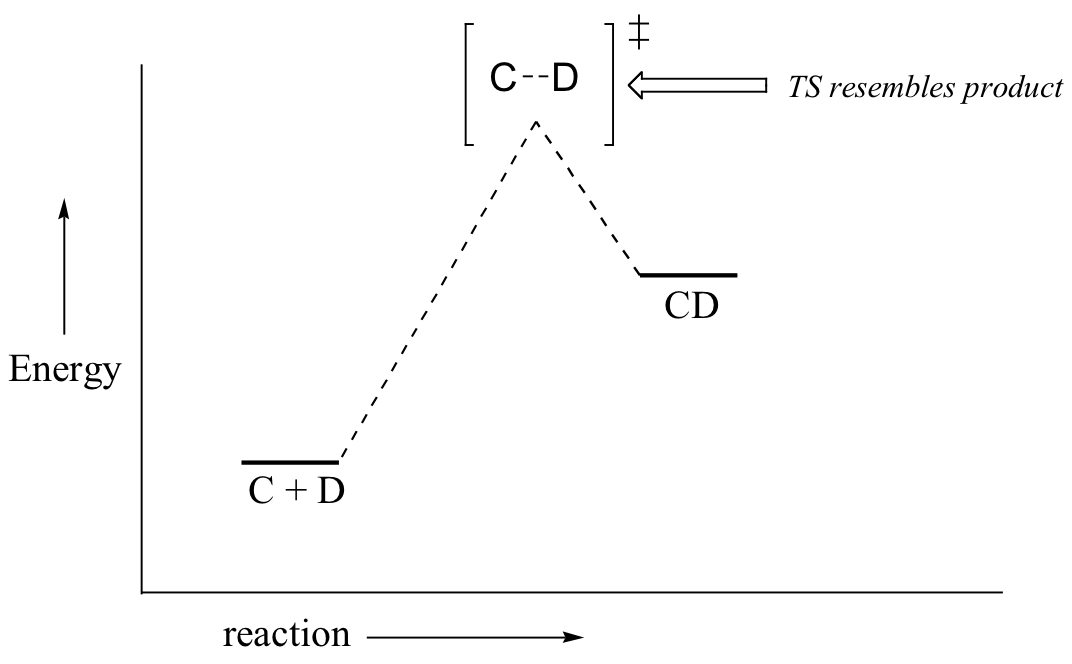
Now, back to transition states. Chemists are often very interested in trying to learn about what the transition state for a given reaction looks like, but addressing this question requires an indirect approach because the transition state itself cannot be observed. In order to gain some insight into what a particular transition state looks like, chemists often invoke the Hammond postulate, which states that a transition state resembles the structure of the nearest stable species. For an exergonic reaction, therefore, the transition state resembles the reactants more than it does the products.
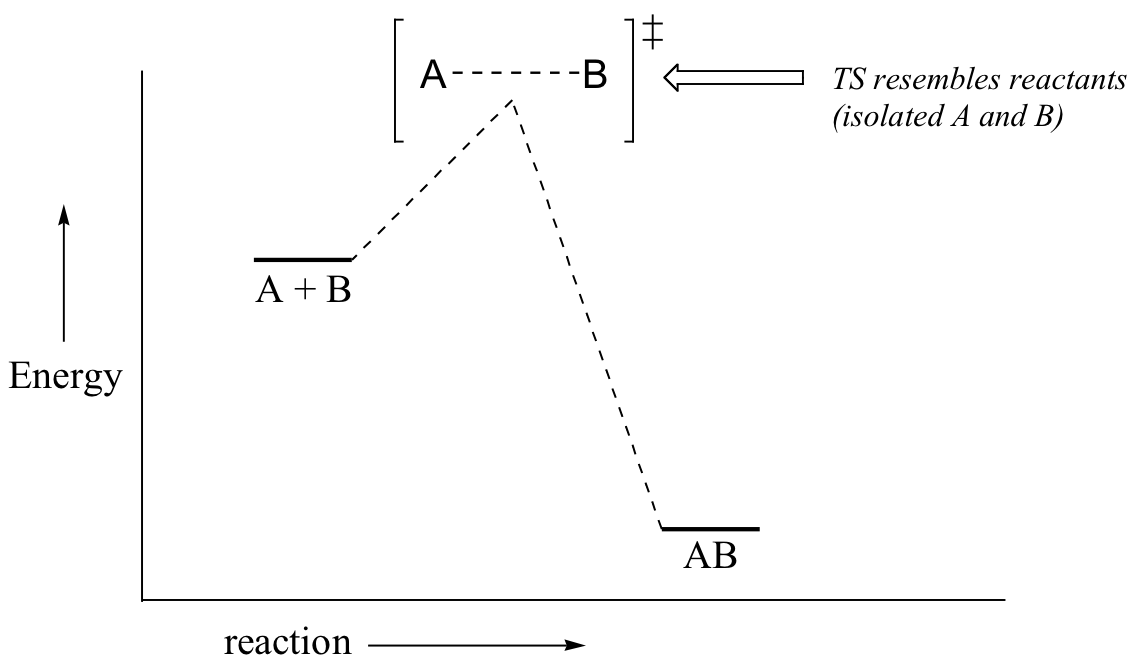
If we consider a hypothetical exergonic reaction between compounds A and B to form AB, the distance between A and B would be relatively large at the transition state, resembling the starting state where A and B are two isolated species. In the hypothetical endergonic reaction between C and D to form CD, however, the bond formation process would be much further along at the TS point, resembling the product.
Now, let’s turn our attention to a two-step reaction mechanism, such as our SN1 reaction between hydroxide and tert-butyl chloride. The energy diagram looks somewhat different:
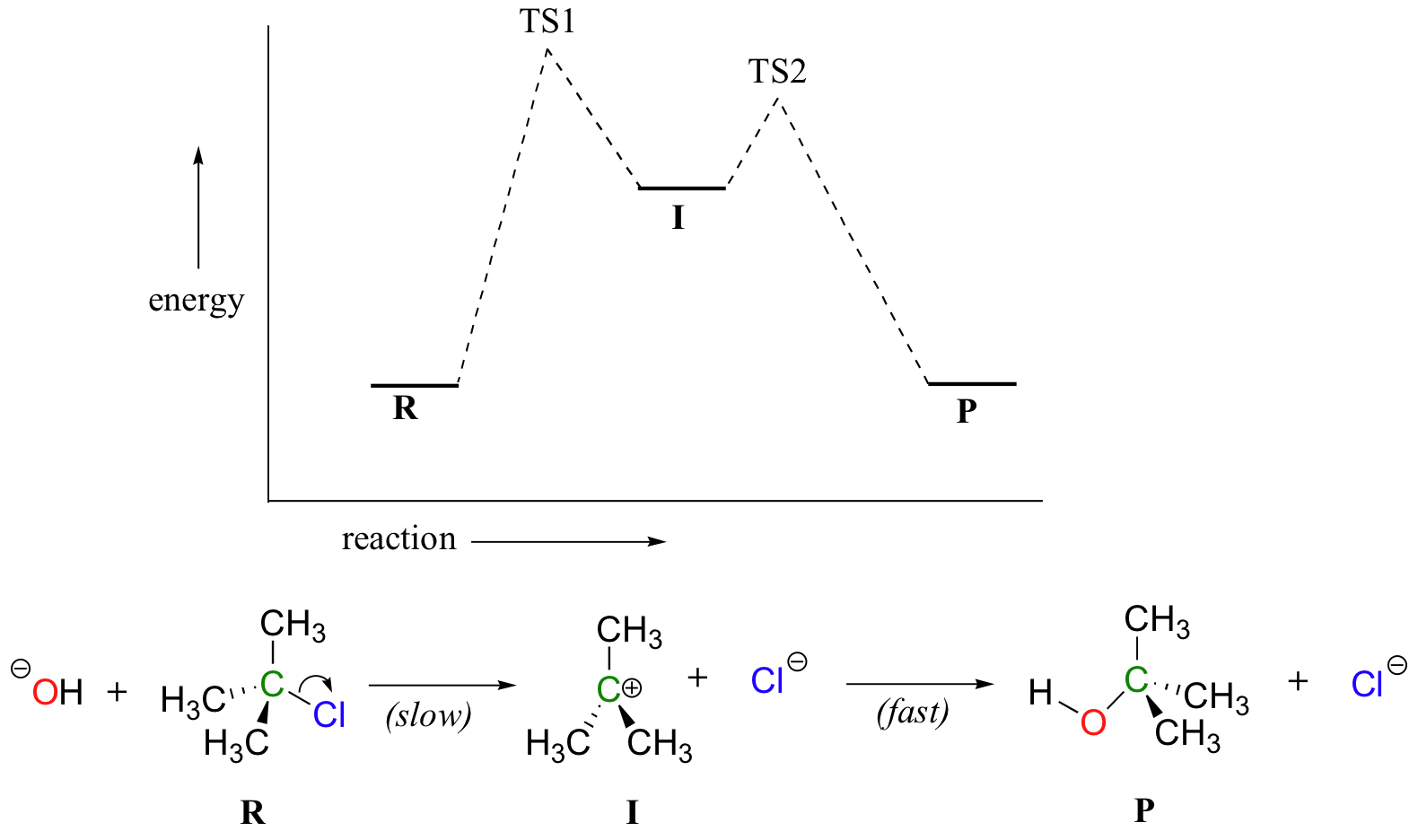
Because there are two steps involved, there are also two transition states and two activation energies to consider, as well as the carbocation intermediate. The first, bond-breaking step from R to I can be depicted as a highly endergonic reaction, because the carbocation-chloride ion pair is significantly less stable (higher in energy) than the starting state. The transition state for this step, labeled TS1, can be thought of as that point at which the carbon-chlorine bond is halfway broken. The second step, attack on the carbocation electrophile by the hydroxide nucleophile and formation of the new carbon-oxygen bond, is a highly exergonic step that passes through a second, much lower transition state TS2. The intermediate (I) is thus depicted as an energy valley situated between TS1 and TS2. According to Hammond’s postulate, both TS1 and TS2 in this reaction should resemble the intermediate I more than either the reactants or products, because in both cases the intermediate is the structure that is closest in energy. This idea – that an intermediate species resembles the nearby transition states - is a very important point to keep in mind, and we will revisit it several times throughout this text as we consider various organic reaction mechanisms.
There is one more very important idea expressed by the energy diagram that relates to the kinetics of the reaction. The activation energy for step 1 is much higher than the activation energy for step 2, meaning that step 1 is slower than step 2. This should make intuitive sense, because step 1 involves bond-breaking and separation of charge, while step 2 involves bond-forming and neutralization of charge. Because step 1 is slow and step 2 is fast, the overall rate of the reaction depends only on the rate of step 1. Step 1 is the ‘rate-determining step’; it is the bottleneck for the overall process. Anything that speeds up the rate of step 2 will not have any effect on the overall rate of the reaction.
Notice also that the rate-determining step involves only one of the two reactants: tert-butyl chloride breaks apart in this step, while hydroxide is not involved at all (contrast this to the SN2 reaction, where the single concerted step involves the collision of two species). The SN1 reaction has first order kinetics, and the rate depends only on the rate constant k and the concentration of tert-butyl chloride:
rate = k[tert-butyl chloride]
What this means is that if we double the rate of tert-butyl chloride, the rate of the reaction will also double. Doubling the hydroxide ion concentration, however, will have no effect on the rate, because hydroxide only participates in the fast, non-rate-determining step.
When thinking about any chemical reaction, it is very important not to confuse the two fundamental chemical concepts of thermodynamics and kinetics. A ‘downhill’, energy-releasing reaction can have a low activation energy and be very fast (our HCl + OH- example is a good case in point). A downhill reaction could also have a high activation energy and be very slow. Think of sugar: you know that sucrose is a high energy molecule and that you obtain lots of energy when you eat it and convert it to carbon dioxide and water, but you also know that sugar sitting in a bowl does not just spontaneously dissipate into carbon dioxide and water before your eyes. This process, although downhill in terms of thermodynamics, occurs very slowly in the absence of heat or catalysts.
Exercise 6.3
Draw a two-dimensional representation of the transition state of each step in the reaction below (this is a reaction that you do not need to understand in detail now - we will study it in chapter 13).