1.3: Atomic Structure - Electron Configurations
- Page ID
- 31370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to write the ground-state electron configuration for each of the elements up to and including atomic number 36.
Make certain that you can define, and use in context, the key terms below.
- ground-state electronic configuration
- Hund's rule
- Pauli exclusion principle
- aufbau principle
The electron configuration of an atom is the representation of the arrangement of electrons distributed among the orbital shells and subshells. Commonly, the electron configuration is used to describe the orbitals of an atom in its ground state, but it can also be used to represent an atom that has ionized into a cation or anion by compensating with the loss of or gain of electrons in their subsequent orbitals. Many of the physical and chemical properties of elements can be correlated to their unique electron configurations. The valence electrons, electrons in the outermost shell, are the determining factor for the unique chemistry of the element.
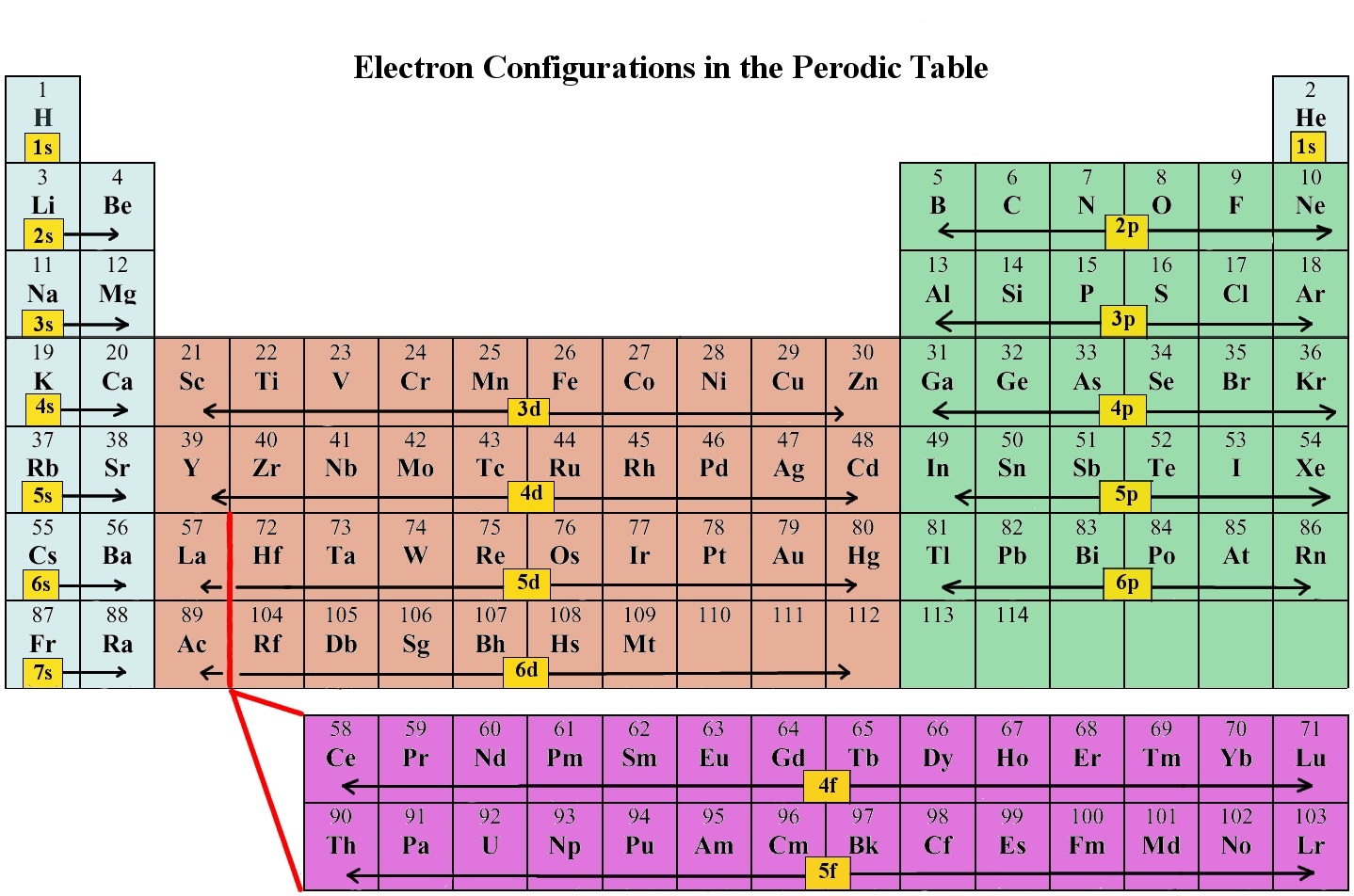
Electron Configurations
The electron configuration of an atom is the representation of the arrangement of electrons distributed among the orbital shells and subshells. Commonly, the electron configuration is used to describe the orbitals of an atom in its ground state, but it can also be used to represent an atom that has ionized into a cation or anion by compensating with the loss of or gain of electrons in their subsequent orbitals. Many of the physical and chemical properties of elements can be correlated to their unique electron configurations. The valence electrons, electrons in the outermost shell, are the determining factor for the unique chemistry of the element.
Before assigning the electrons of an atom into orbitals, one must become familiar with the basic concepts of electron configurations. Every element on the periodic table consists of atoms, which are composed of protons, neutrons, and electrons. Electrons exhibit a negative charge and are found around the nucleus of the atom in electron orbitals, defined as the volume of space in which the electron can be found within 95% probability. The four different types of orbitals (s,p,d, and f) have different shapes, and one orbital can hold a maximum of two electrons. The p, d, and f orbitals have different sublevels, thus can hold more electrons.
As stated, the electron configuration of each element is unique to its position on the periodic table. The energy level is determined by the period and the number of electrons is given by the atomic number of the element. Orbitals on different energy levels are similar to each other, but they occupy different areas in space. The 1s orbital and 2s orbital both have the characteristics of an s orbital (radial nodes, spherical volume probabilities, can only hold two electrons, etc.) but, as they are found in different energy levels, they occupy different spaces around the nucleus. Each orbital can be represented by specific blocks on the periodic table. The s-block is the region of the alkali metals including helium (Groups 1 & 2), the d-block are the transition metals (Groups 3 to 12), the p-block are the main group elements from Groups 13 to 18, and the f-block are the lanthanides and actinides series.
Using the periodic table to determine the electron configurations of atoms is key, but also keep in mind that there are certain rules to follow when assigning electrons to different orbitals. The periodic table is an incredibly helpful tool in writing electron configurations. For more information on how electron configurations and the periodic table are linked, visit the Connecting Electrons to the Periodic Table module.
Rules for Assigning Electron Orbitals
Pauli Exclusion Principle
The Pauli exclusion principle states that no two electrons can have the same four quantum numbers. The first three (n, l, and ml) may be the same, but the fourth quantum number must be different. A single orbital can hold a maximum of two electrons, which must have opposing spins; otherwise they would have the same four quantum numbers, which is forbidden. One electron is spin up (ms = +1/2) and the other would spin down (ms = -1/2). This tells us that each subshell has double the electrons per orbital. The s subshell has 1 orbital that can hold up to 2 electrons, the p subshell has 3 orbitals that can hold up to 6 electrons, the d subshell has 5 orbitals that hold up to 10 electrons, and the f subshell has 7 orbitals with 14 electrons.
The first three quantum numbers of an electron are n=1, l=0, ml=0. Only two electrons can correspond to these, which would be either ms = -1/2 or ms = +1/2. As we already know from our studies of quantum numbers and electron orbitals, we can conclude that these four quantum numbers refer to the 1s subshell. If only one of the ms values are given then we would have 1s1 (denoting hydrogen) if both are given we would have 1s2 (denoting helium). Visually, this is be represented as:
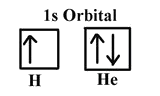
As shown, the 1s subshell can hold only two electrons and, when filled, the electrons have opposite spins.
Hund's Rule
When assigning electrons in orbitals, each electron will first fill all the orbitals with similar energy (also referred to as degenerate) before pairing with another electron in a half-filled orbital. Atoms at ground states tend to have as many unpaired electrons as possible. When visualizing this processes, think about how electrons are exhibiting the same behavior as the same poles on a magnet would if they came into contact; as the negatively charged electrons fill orbitals they first try to get as far as possible from each other before having to pair up.
If we look at the correct electron configuration of the Nitrogen (Z = 7) atom, a very important element in the biology of plants: 1s2 2s2 2p3
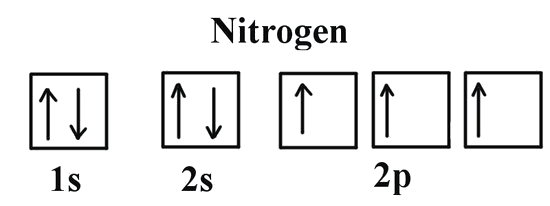
We can clearly see that p orbitals are half-filled as there are three electrons and three p orbitals. This is because Hund's Rule states that the three electrons in the 2p subshell will fill all the empty orbitals first before filling orbitals with electrons in them. If we look at the element after nitrogen in the same period, oxygen (Z = 8) its electron configuration is: 1s2 2s2 2p4 (for an atom).
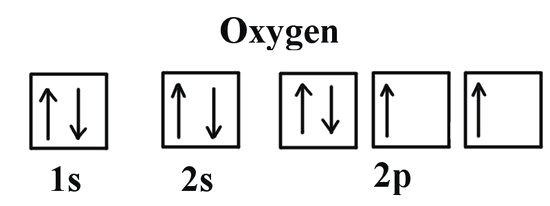
Oxygen has one more electron than nitrogen and as the orbitals are all half filled the electron must pair up.
Occupation of Orbitals
Electrons fill orbitals in a way to minimize the energy of the atom. Therefore, the electrons in an atom fill the principal energy levels in order of increasing energy (the electrons are getting farther from the nucleus). The relative energy of the orbitals is shown in Figure \(\PageIndex{2}\)
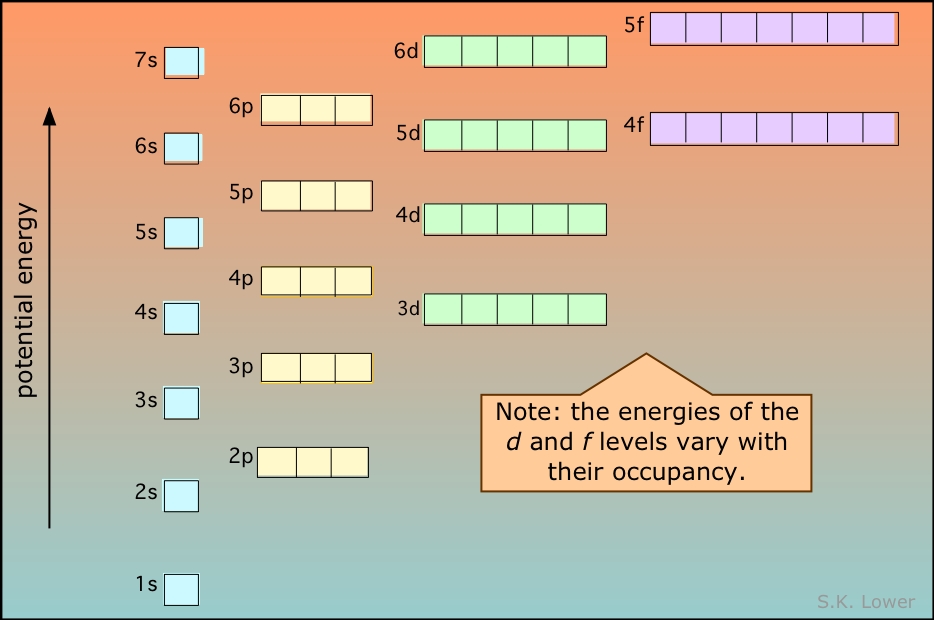
The order of levels filled is then:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and 7p
The general order in which orbitals are filled is depicted in Figure \(\PageIndex{3}\). Subshells corresponding to each value of n are written from left to right on successive horizontal lines, where each row represents a row in the periodic table. The order in which the orbitals are filled is indicated by the diagonal lines running from the upper right to the lower left. Accordingly, the 4s orbital is filled prior to the 3d orbital because of shielding and penetration effects. Consequently, the electron configuration of potassium, which begins the fourth period, is [Ar]4s1, and the configuration of calcium is [Ar]4s2. Five 3d orbitals are filled by the next 10 elements, the transition metals, followed by three 4p orbitals. Notice that the last member of this row is the noble gas krypton (Z = 36), [Ar]4s23d104p6 = [Kr], which has filled 4s, 3d, and 4p orbitals. The fifth row of the periodic table is essentially the same as the fourth, except that the 5s, 4d, and 5p orbitals are filled sequentially.
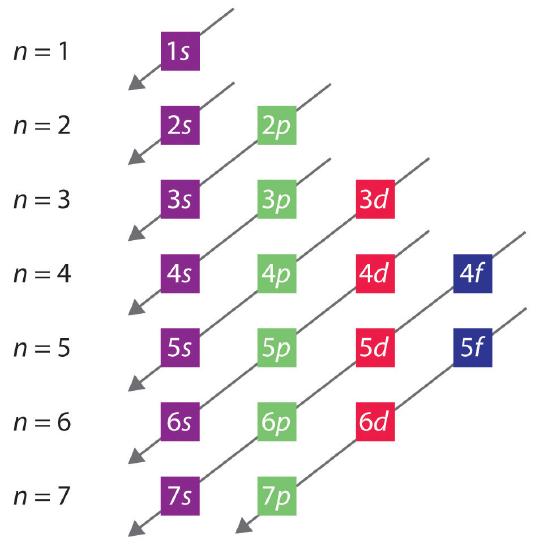
The Aufbau Process
Aufbau comes from the German word "aufbauen" meaning "to build." When writing electron configurations, orbitals are built up from atom to atom. When writing the electron configuration for an atom, orbitals are filled in order of increasing atomic number. However, there are some exceptions to this rule.
Following the pattern across a period from B (Z=5) to Ne (Z=10), the number of electrons increases and the subshells are filled. This example focuses on the p subshell, which fills from boron to neon.
- B (Z=5) configuration: 1s2 2s2 2p1
- C (Z=6) configuration:1s2 2s2 2p2
- N (Z=7) configuration:1s2 2s2 2p3
- O (Z=8) configuration:1s2 2s2 2p4
- F (Z=9) configuration:1s2 2s2 2p5
- Ne (Z=10) configuration:1s2 2s2 2p6
The Number of Valence Electrons
The number of valence electrons of an element can be determined by the periodic table group (vertical column) in which the element is categorized. With the exception of groups 3–12 (the transition metals), the units digit of the group number identifies how many valence electrons are associated with a neutral atom of an element listed under that particular column. For example in group 16, the units digit is 6 and elements in this group have 6 valence electrons.
| Periodic table group | Valence electrons |
|---|---|
| Group 1: alkali metals | 1 |
| Group 2: alkaline earth metals | 2 |
| Groups 3-12: transition metals | 2* (The 4s shell is complete and cannot hold any more electrons) |
| Group 13: boron group | 3 |
| Group 14: carbon group | 4 |
| Group 15: pnictogens | 5 |
| Group 16: chalcogens | 6 |
| Group 17: halogens | 7 |
| Group 18: noble gases | 8** |
* The general method for counting valence electrons is generally not useful for transition metals. Instead the modified d electron count method is used.
** Except for helium, which has only two valence electrons.
The electron configuration of an element is the arrangement of its electrons in its atomic orbitals. By knowing the electron configuration of an element, we can predict and explain a great deal of its chemistry.
Draw an orbital diagram and use it to derive the electron configuration of phosphorus, Z = 15. What is its valence electron configuration?
Given: atomic number
Asked for: orbital diagram and valence electron configuration for phosphorus
Strategy:
- Locate the nearest noble gas preceding phosphorus in the periodic table. Then subtract its number of electrons from those in phosphorus to obtain the number of valence electrons in phosphorus.
- Referring to Figure 1.3.1, draw an orbital diagram to represent those valence orbitals. Following Hund’s rule, place the valence electrons in the available orbitals, beginning with the orbital that is lowest in energy. Write the electron configuration from your orbital diagram.
- Ignore the inner orbitals (those that correspond to the electron configuration of the nearest noble gas) and write the valence electron configuration for phosphorus.
Solution:
A Because phosphorus is in the third row of the periodic table, we know that it has a [Ne] closed shell with 10 electrons. We begin by subtracting 10 electrons from the 15 in phosphorus.
B The additional five electrons are placed in the next available orbitals, which Figure 1.2.5 tells us are the 3s and 3p orbitals:
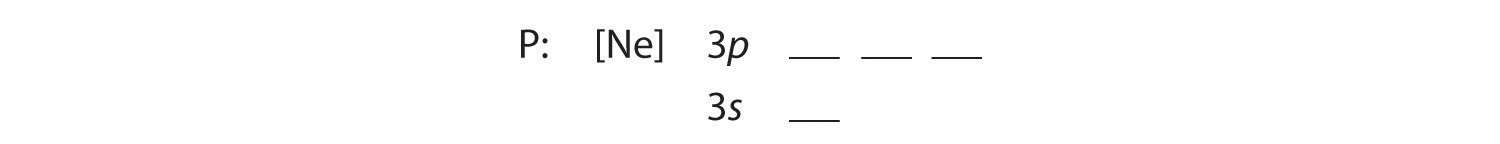
Because the 3s orbital is lower in energy than the 3p orbitals, we fill it first:
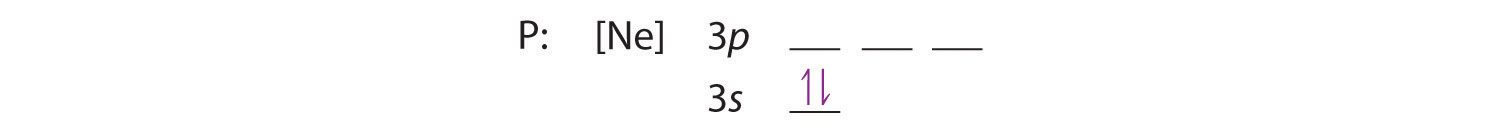
Hund’s rule tells us that the remaining three electrons will occupy the degenerate 3p orbitals separately but with their spins aligned:
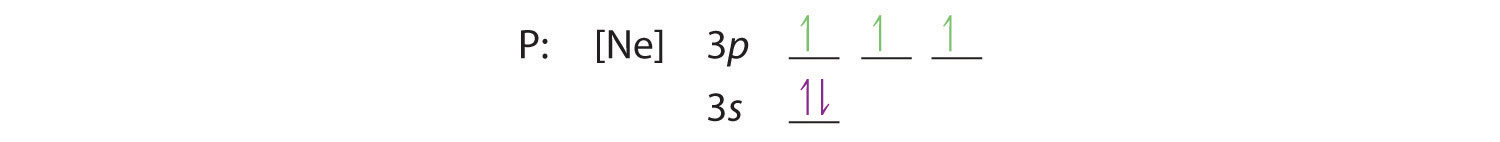
The electron configuration is [Ne]3s23p3.
C We obtain the valence electron configuration by ignoring the inner orbitals, which for phosphorus means that we ignore the [Ne] closed shell. This gives a valence-electron configuration of 3s23p3.
Draw an orbital diagram and use it to derive the electron configuration of chlorine, Z = 17. What is its valence electron configuration?
- Answer
- [Ne]3s23p5; 3s23p5
The sixth row of the periodic table will be different from the preceding two because the 4f orbitals, which can hold 14 electrons, are filled between the 6s and the 5d orbitals. The elements that contain 4f orbitals in their valence shell are the lanthanides. When the 6p orbitals are finally filled, we have reached the next (and last known) noble gas, radon (Z = 86), [Xe]6s24f145d106p6 = [Rn]. In the last row, the 5f orbitals are filled between the 7s and the 6d orbitals, which gives the 14 actinide elements. Because the large number of protons makes their nuclei unstable, all the actinides are radioactive.
Write the electron configuration of mercury (Z = 80), showing all the inner orbitals.
Given: atomic number
Asked for: complete electron configuration
Strategy:
Using the orbital diagram in Figure \(\PageIndex{3}\) and the periodic table as a guide, fill the orbitals until all 80 electrons have been placed.
Solution:
By placing the electrons in orbitals following the order shown in Figure \(\PageIndex{3}\) and using the periodic table as a guide, we obtain
| 1s2 | row 1 | 2 electrons |
| 2s22p6 | row 2 | 8 electrons |
| 3s23p6 | row 3 | 8 electrons |
| 4s23d104p6 | row 4 | 18 electrons |
| 5s24d105p6 | row 5 | 18 electrons |
| row 1–5 | 54 electrons |
After filling the first five rows, we still have 80 − 54 = 26 more electrons to accommodate. According to Figure 1.3.1, we need to fill the 6s (2 electrons), 4f (14 electrons), and 5d (10 electrons) orbitals. The result is mercury’s electron configuration:
1s22s22p63s23p64s23d104p65s24d105p66s24f145d10 = Hg = [Xe]6s24f145d10
with a filled 5d subshell, a 6s24f145d10 valence shell configuration, and a total of 80 electrons. (You should always check to be sure that the total number of electrons equals the atomic number.)
Summary
Based on the Pauli principle and a knowledge of orbital energies obtained using hydrogen-like orbitals, it is possible to construct the periodic table by filling up the available orbitals beginning with the lowest-energy orbitals (the aufbau principle), which gives rise to a particular arrangement of electrons for each element (its electron configuration). Hund’s rule says that the lowest-energy arrangement of electrons is the one that places them in degenerate orbitals with their spins parallel. For chemical purposes, the most important electrons are those in the outermost principal shell, the valence electrons.

