25.2: Depicting Carbohydrate Stereochemistry - Fischer Projections

Objectives

After completing this section, you should be able to

1. draw the Fischer projection of a monosaccharide, given its wedge and dash structure or a molecular model.
2. draw the wedge and dash structure of a monosaccharide, given its Fischer projection or a molecular model.
3. construct a molecular model of a monosaccharide, given its Fischer projection or wedge and dash structure.

Key Terms

Make certain that you can define, and use in context, the key term below.

• Fischer projection

Study Notes

When studying this section, use your molecular model set to assist you in visualizing the structures of the compounds that are discussed. It is important that you be able to determine whether two apparently different Fischer projections represent two different structures or one single structure. Often the simplest way to check is to construct a molecular model corresponding to each projection formula, and then compare the two models.

Drawing Representations of 3D Structures

The problem of drawing three-dimensional configurations on a two-dimensional surface, such as a piece of paper, has been a long-standing concern of chemists. The wedge and dash notations we have been using are effective, but can be troublesome when applied to compounds having many chiral centers. As part of his Nobel Prize-winning research on carbohydrates, the great German chemist Emil Fischer, devised a simple notation that is still widely used. Fischer Projections allow us to represent 3D molecular structures in a 2D environment without changing their properties and/or structural integrity.

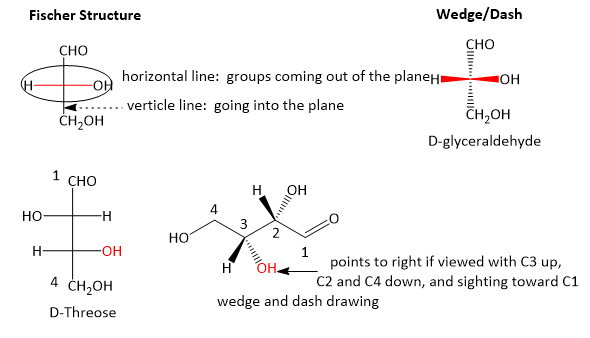
Fisher projections show sugars in their open chain form. In a Fischer projection, the carbon atoms of a sugar molecule are connected vertically by solid lines, while carbon-oxygen and carbon-hydrogen bonds are shown horizontally. Stereochemical information is conveyed by a simple rule: vertical bonds point into the plane of the page, while horizontal bonds point out of the page.

Sugars can be drawn in the straight chain form as either Fisher projections or perspective structural formulas. When drawing Fischer projections, the aldehyde group is written at the top, and the H and OH groups that are attached to each chiral carbon are written to the right or left. The arrangement of the atoms distinguishes one stereoisomer from the other.

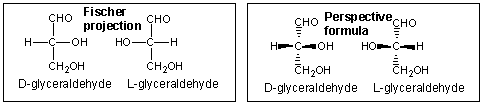
Below are two different representations of (R)-glyceraldehyde, the smallest sugar molecule (also called D-glyceraldehyde in the stereochemical nomenclature used for sugars):

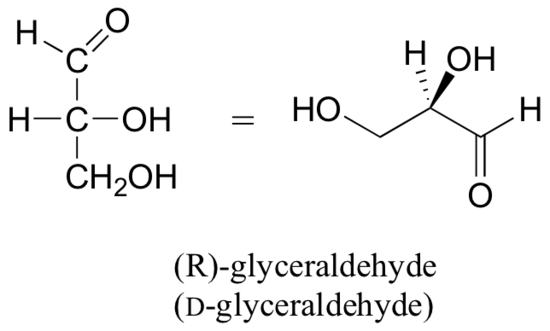
In the Fisher projection, the vertical bonds point down into the plane of the paper. That's easy to visualize for 3C molecules. but more complicated for bigger molecules. For those draw a wedge and dash line drawing of the molecule. When determining the orientation of the hydroxides on each C, orient the wedge and dash drawing in your mind so that the C atoms adjacent to the one of interest are pointing down. Sighting towards the carbonyl C, if the OH is pointing to the right in the Fisher project, it should be pointing to the right in the wedge and dash drawing, as shown below for D-erthyrose and D-glucose.

Below are three representations of the open chain form of D-glucose: in the conventional Fischer projection, a wedge/dash version of a Fischer projection, and finally in the 'zigzag' style that is preferred by many organic chemists.

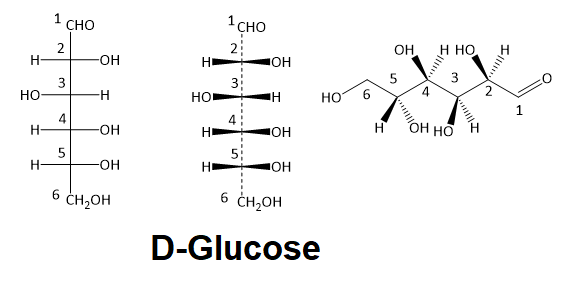
Fischer projections are useful when looking at many different diastereomeric sugar structures, because the eye can quickly pick out stereochemical differences according to whether a hydroxyl group is on the left or right side of the structure.

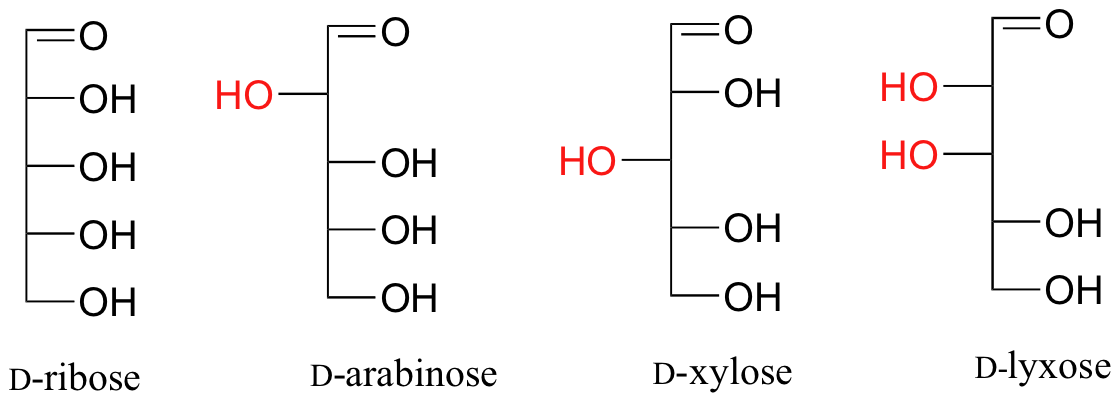
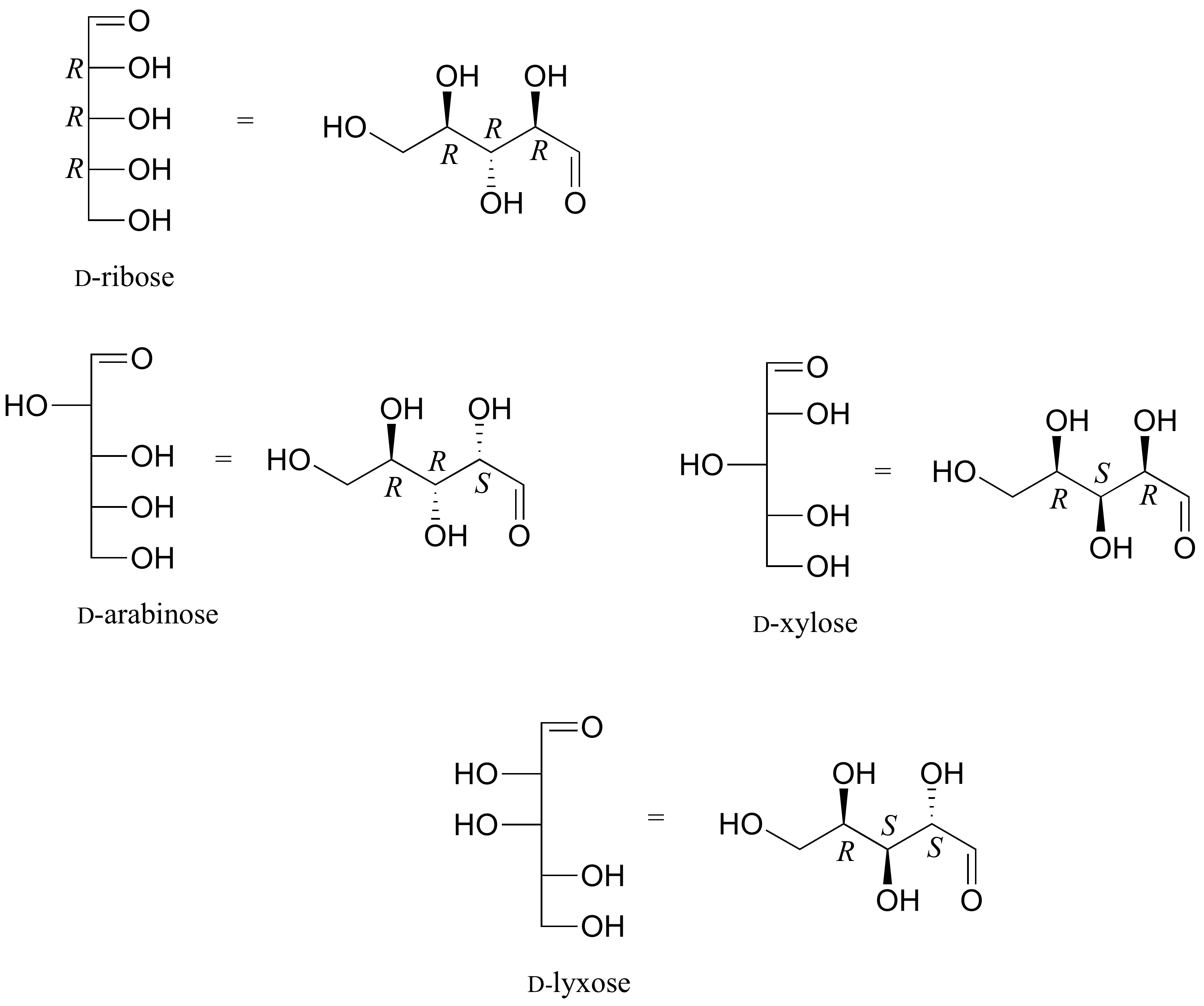
The usefulness of this notation to Fischer, in his carbohydrate studies, is evident in the following diagram. There are eight stereoisomers of 2,3,4,5-tetrahydroxypentanal, a group of compounds referred to as the aldopentoses (aldo- since the oxidized carbon is an aldehyde and -pentose since the molecules contain 5 carbons). Since there are three chiral centers in this constitution, we should expect a maximum of 2³ stereoisomers. These eight stereoisomers consist of four sets of enantiomers. If the configuration at C-4 is kept constant (R in the examples shown here), the four stereoisomers that result will be diastereomers.

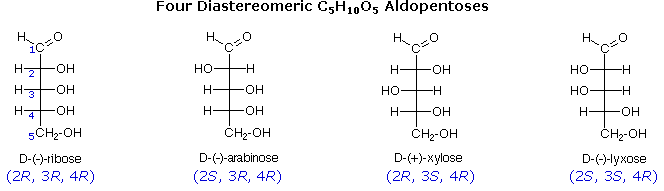
The aldopentose structures drawn above are all diastereomers. A more selective term, epimer, is used to designate diastereomers that differ in configuration at only one chiral center. Thus, ribose and arabinose are epimers at C-2, and arabinose and lyxose are epimers at C-3. However, arabinose and xylose are not epimers, since their configurations differ at both C-2 and C-3.

The Fisher structures of the most common monosaccharides (other than glyceraldehyde and dihydroxyacetone), which you will encounter most frequently are shown below.

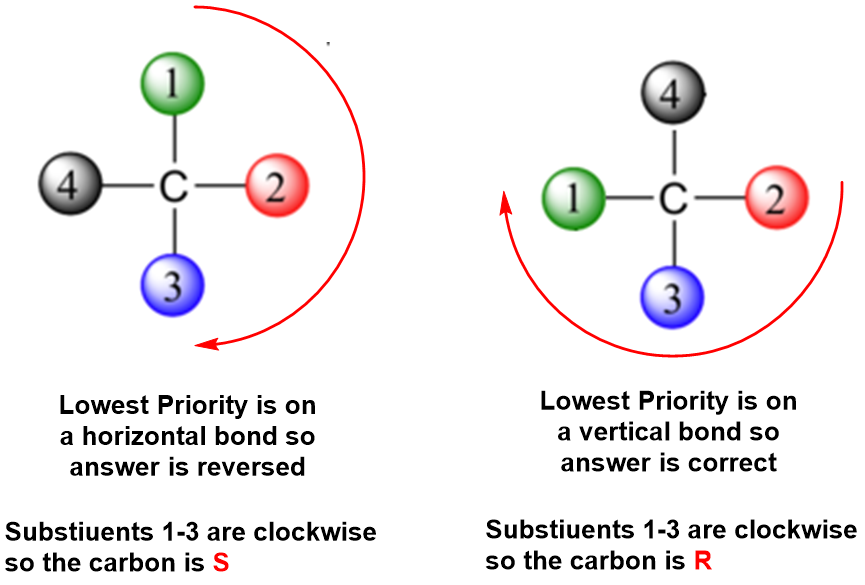
Determining R and S in Fischer Projections

Determining whether a chiral carbon is R or S may seem difficult when using Fischer projections, but it is actually quite simple. If the lowest priority group (often a hydrogen) is on a vertical bond, the configuration is given directly from the relative positions of the three higher-ranked substituents. If the lowest priority group is on a horizontal bond, the positions of the remaining groups give the wrong answer (you are in looking at the configuration from the wrong side), so you simply reverse it.

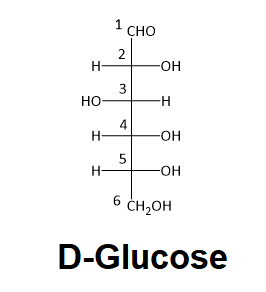
Worked Example \(\PageIndex{1}\)

Determine if carbon #2 in D-glucose is R or S.

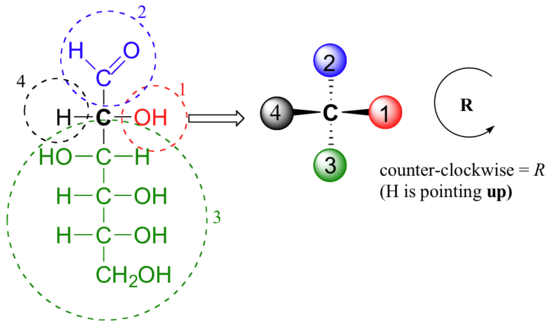
Answer

When deciding whether a stereocenter in a Fischer projection is R or S, realize that the hydrogen, in a horizontal bond. Therefore, the orientation of the three remaining substituents is reversed to create the correct answer or a counterclockwise circle means R, and a clockwise circle means S. For carbon #2 in D-Glucose substituent 1, 2, and 3 form a counterclockwise circle so the carbon is R.

How to make Fischer Projections

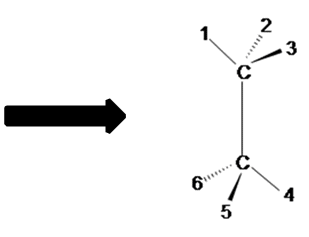
To make a Fischer Projection, it is easier to show through examples than through words. Lets start with the first example, turning a 3D structure of ethane into a 2D Fischer Projection.

Exercise \(\PageIndex{1}\)

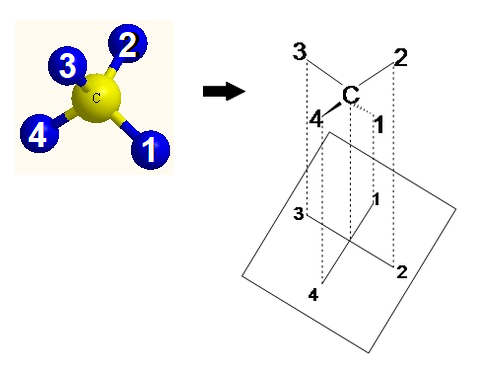
Start by mentally converting a 3D structure into a Dashed-Wedged Line Structure. Remember, the atoms that are pointed toward the viewer would be designated with a wedged lines and the ones pointed away from the viewer are designated with dashed lines.

Figure B

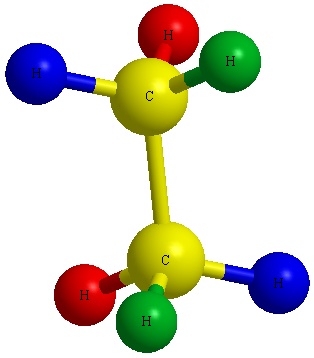
Notice the red balls (atoms) in Figure A above are pointed away from the screen. These atoms will be designated with dashed lines like those in Figure B by number 2 and 6. The green balls (atoms) are pointed toward the screen. These atoms will be designated with wedged lines like those in Figure B by number 3 and 5. The blue atoms are in the plane of the screen so they are designated with straight lines.

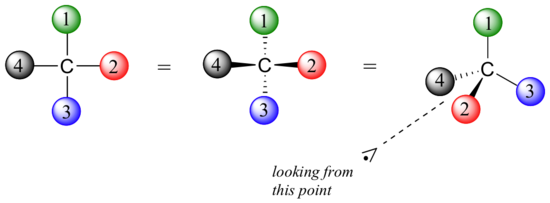
Now that we have our Dashed- Wedged Line Structure, we can convert it to a Fischer Projection. However, before we can convert this Dashed-Wedged Line Structure into a Fischer Projection, we must first convert it to a “flat” Dashed-Wedged Line Structure. Then from there we can draw our Fischer Projection. Lets start with a more simpler example. Instead of using the ethane shown in Figure A and B, we will start with a methane. The reason being is that it allows us to only focus on one central carbon, which make things a little bit easier.

Figure D

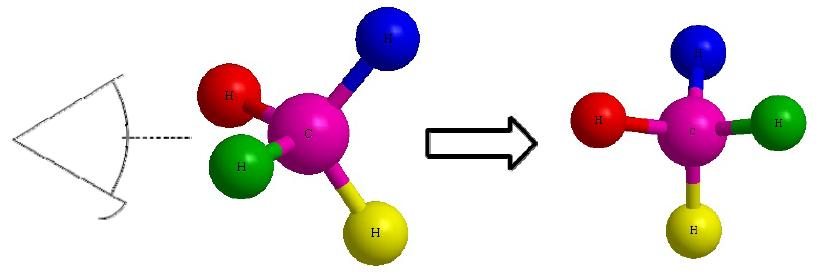
Lets start with this 3D image and work our way to a dashed-wedged image. Start by imagining yourself looking directly at the central carbon from the left side as shown in Figure C. It should look something like Figure D. Now take this Figure D and flatten it out on the surface of the paper and you should get an image of a cross.

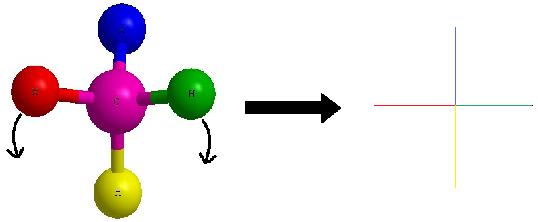
As a reminder, the horizontal line represents atoms that are coming out of the paper and the vertical line represents atoms that are going into the paper. The cross image to the right of the arrow is a Fischer projection.

Exercise \(\PageIndex{1}\)

Draw 'zigzag' structures (using the solid/dash wedge convention to show stereochemistry) for the four sugars in the figure below. Label all stereocenters R or S.

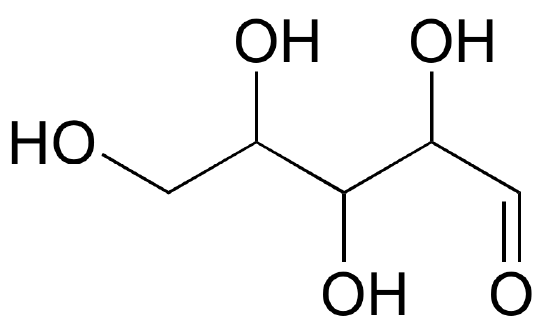
Answer