9.11: Nuclear Magnetic Resonance Spectroscopy
- Page ID
- 22228
Nuclear magnetic resonance (NMR) spectroscopy is extremely useful for identification and analysis of organic compounds. The principle on which this form of spectroscopy is based is simple. The nuclei of many kinds of atoms act like tiny magnets and tend to become aligned in a magnetic field. In NMR spectroscopy, we measure the energy required to change the alignment of magnetic nuclei in a magnetic field. To illustrate the procedure with a simple example, consider the behavior of a proton \(\left( ^1H \right)\) in a magnetic field. There are two possible alignments of this magnetic nucleus with respect to the direction of the applied field, as shown in Figure 9-21. The nuclear magnets can be aligned either with the field direction, or opposed to it. The two orientations are not equivalent, and energy is required to change the more stable alignment to the less stable alignment.

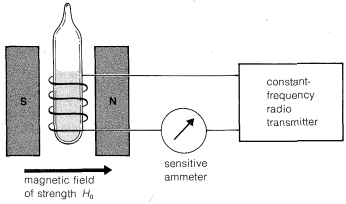
A schematic diagram of an NMR instrument is shown in Figure 9-22. When a substance such as ethanol, \(CH_3-CH_2-OH\), the hydrogens of which have nuclei (protons) that are magnetic, is placed in the transmitter coil and the magnetic field is increased gradually, at certain field strengths radio-frequency energy is absorbed by the sample and the ammeter indicates an increase in the flow of current in the coil. The overall result is a spectrum such as the one shown in Figure 9-23. This spectrum is detailed enough to serve as a useful "fingerprint" for ethanol, and also is simple enough that we will be able to account for the origin of each line. It is the purpose of this section to explain how the complexities of spectra such as that of Figure 9-23 can be interpreted in terms of chemical structure.
For what kinds of substances can we expect nuclear magnetic resonance absorption to occur? Magnetic properties always are found with nuclei of odd-numbered masses, \(^1H\), \(^{13}C\), \(^{15}N\), \(^{17}O\), \(^{19}F\), \(^{31}P\), and so on, as well as for nuclei of even mass but odd atomic number, \(^2H\), \(^{10}B\), \(^{14}N\), and so on.\(^8\) Nuclei such as \(^{12}C\), \(^{16}O\), and \(^{32}S\), which have even mass and atomic numbers, have no magnetic properties and do not give nuclear magnetic resonance signals. For various reasons, routine use of NMR spectra in organic chemistry is confined to \(^1H\), \(^{19}F\), \(^{13}C\), and \(^{31}P\). We shall be concerned in this chapter only with NMR spectra of hydrogen (\(^1H\)) and of carbon (\(^{13}C\)).
The kind of NMR spectroscopy we shall discuss here is limited in its applications because it can be carried out only with liquids or solutions. Fortunately, the allowable range of solvents is large, from hydrocarbons to concentrated sulfuric acid, and for most compounds it is possible to find a suitable solvent.
Nuclear magnetic resonance spectra may be so simple as to have only a single absorption peak, but they also can be much more complex than the spectrum of Figure 9-23. However, it is important to recognize that no matter how complex an NMR spectrum appears to be, in involves just three parameters: chemical shifts, spin-spin splittings, and kinetic (reaction-rate) processes. We shall have more to say about each of these later. First, let us try to establish the relationship of NMR spectroscopy to some of the other forms of spectroscopy we have already discussed in this chapter.
The Relation of NMR to Other Kinds of Spectroscopy
Nuclear magnetic resonance\(^9\) spectroscopy involves transitions between possible energy levels of magnetic nuclei in an applied magnetic field (see Figure 9-21). The transition energies are related to the frequency of the absorbed radiation by the familiar equation \(\Delta E - h \nu\). An important difference between nmr and other forms of spectroscopy is that \(\Delta E\) is influenced by the strength of the applied field. This should not be surprising, because if we are to measure the energy of changing the direction of alignment of a magnetic nucleus in a magnetic field, then the stronger the field the more energy will be invloved.
Nuclear spin (symbolized as \(I\)) is a quantized property that correlates with nuclear magnetism such that when \(I\) is zero the nucleus has no spin and no magnetic properties. Examples are \(^{12}C\) and \(^{16}O\). Several nuclei of particular interest to organic chemists - \(^1H\), \(^{13}C\), \(^{15}\), \(^{19}\), and \(^{31}P\) - have spin of \(\frac{1}{2}\). With \(I = \frac{1}{2}\) there are only two magnetic energy states of the nucleus in a magnetic field. These states are designated with the spin quantum numbers \(+ \frac{1}{2}\) and \(- \frac{1}{2}\). The difference in energy between these states, \(\Delta E\), is given by
\[\Delta E = \gamma h H = h \nu\]
or
\[\nu = \gamma H\]
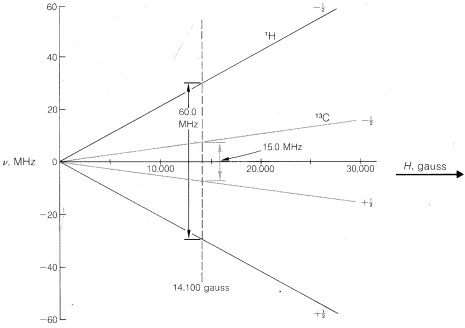
in which \(h\) is Planck's constant, \(\nu\) is in hertz, \(\gamma\) is a nuclear magnetic constant called the gyromagnetic ratio,\(^{10}\), and \(H\) is the magnetic field strength at the nucleus. In general, \(H\) will not be exactly equal to \(H_\text{o}\), the applied magnetic field and, as we will see, this difference leads to important chemical information. Each kind of nucleus (\(^1H\), \(^{13}C\), \(^{15}N\), etc.) has its own \(\gamma\) value and, consequently, will undergo transitions at different frequencies at any particular value of \(H\). This should become clearer by study of Figure 9-24.
There are several modes of operation of an nmr spectrometer. First and most common, we hold \(\nu\) constant and vary (or "sweep") \(H_\text{o}\). Close to \(\nu = \gamma H\), energy is absorbed by the nuclei and the current flow from the transmitter increases until \(\nu\) is exactly equal to \(\gamma H\). Further increase of \(H_\text{o}\) makes \(\nu < \gamma H_\text{o}\) and the current flow decreases. The form of the energy-absorption curve as a function of \(H_\text{o}\) when \(H_\text{o}\) is changed very slowly is shown in Figure 9-25a. The peak is centered on the point where \(\nu = \gamma H\). When \(H_\text{o}\) is changed more rapidly, transient effects are observed on the peak, which are a consequence of the fact that the nuclei do not revert instantly from the \(- \frac{1}{2}\) to \(+ \frac{1}{2}\) state. The resulting

phenomenon is called "ringing" and is shown in Figures 9-25b and 9-25c. Evidence of ringing also will be seen on peaks of Figure 9-23.
An alternative method of running an nmr spectrometer is to hold the magnetic field constant and to sweep the transmitter frequency through the resonances. This mode of operation is more like other forms of spectroscopy and gives the same line shapes as sweeping the field (Figure 9-25).
What energy is associated with a \(^1H\) nmr transition? The magnitude of this energy may be calculated from the relationship between energy and wavelength (frequency) of the absorbed radiation (Section 9-4). That is,
\[\Delta E = \frac{28,600}{\lambda} \text{kcal mol}^{-1}\] and \[\lambda = \frac{c}{\nu}\]
The frequency \(\nu\) is the operating frequency of the spectrometer, which we will take as \(60 \: \text{MHz}\) or \(6 \times 10^7 \: \text{Hz}\) (cycles \(\text{sec}^{-1}\)), and the velocity of light is \(3 \times 10^8 \: \text{m sec}^{-1}\). Hence
\[\lambda = \frac{3 \times 10^8 \times 10^9 \left( \text{nm sec}^{-1} \right)}{6 \times 10^7 \left( \text{Hz} \right)} = 5 \times 10^9 \: \text{nm}\]
and
\[\Delta E = \frac{28,600}{5 \times 10^9} = 5.7 \times 10^{-6} \: \text{kcal mol}^{-1}\]
This is a very small energy difference, which means that only very few more of the nuclei are in the more stable \(+ \frac{1}{2}\) state than in the less stable \(- \frac{1}{2}\) state. The equilibrium constant \(K\) for \(- \frac{1}{2} \rightleftharpoons + \frac{1}{2}\) calculated from Equation 4-2 for \(25^\text{o}\) (298 \: \text{K}\)) and neglecting possible entropy effects is 1.000010!
The Chemical Shift
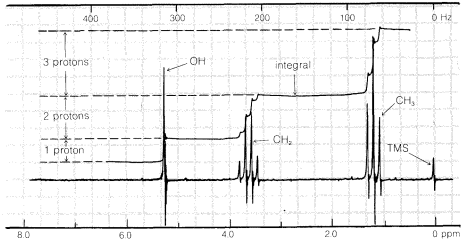
The plot of signal against magnetic field strength for ethanol in Figure 9-23 shows three principal groups of lines corresponding to the three varieties of hydrogen present: methyl (\(CH_3\)), methylene (\(CH_3\)), and hydroxyl (\(OH\)). Differences in the field strengths at which signals are obtained for nuclei of the same kind, such as protons, but located in different molecular environments, are called chemical shifts.
Another very important point to notice about Figure 9-23 is that the intensities of the three principal absorptions are in the ratio of 1:2:3, corresponding to the ratio of the number of each kind of proton (\(OH\), \(CH_2\), \(CH_3\)) producing the signal. In general, areas under the peaks of a spectrum such as in Figure 9-23 are proportional to the number of nuclei in the sample that give those peaks. The areas can be measured by electronic integration and the integral often is displayed on the chart, as it is in Figure 9-23, as a stepped line increasing from left to right. The height of each step corresponds to the relative number of nuclei of a particular kind. Unless special precautions are taken, integrals usually should not be considered accurate to better than about \(5\%\).
Why do protons in different molecular environments absorb at different field strengths? The field strength \(H\) at a particular nucleus is less than the strength of the external magnetic field \(H_\text{o}\). This is because the valence electrons around a particular nucleus and around neighboring nuclei respond to the applied magnetic field so as to shield the nucleus from the applied field. The way this shielding occurs is as follows.
First, when an atom is placed in a magnetic field, its electrons are forced to undergo a rotation about the field axis, as shown in Figure 9-26. Second,
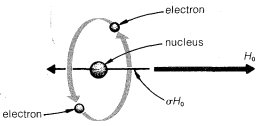
rotation of the electrons around the nucleus is a circulation of charge, and this creates a small magnetic field at the nucleus opposite in the direction to \(H_\text{o}\). Third, the magnitude of this diamagnetic\(^{11}\) effect is directly proportional to \(H_\text{o}\) and can be quantified as \(\sigma H_\text{o}\), in which \(\sigma\) is the proportionality constant. It is important to recognize that \(\sigma\) is not a nuclear property but depends on the chemical environment of the atom. Each chemically different proton will have a different value of \(\sigma\) and hence a different chemical shift.
The actual field \(H\) at the nucleus will be \(H_\text{o} - \sigma H_\text{o}\). Because \(\sigma\) acts to reduce the strength of the applied field at the nucleus, it is called the magnetic shielding parameter. The more shielding there is, the stronger the applied field must be to satisfy the resonance condition,
Common usage is: upfield, more shielding; downfield, less shielding; and you should remember that field-sweep spectra always are recorded with the field increasing from left to right.
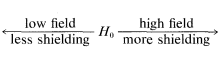
Chemical Shift and Stereochemistry
The value of nmr spectroscopy in structure determination lies in the fact that chemically different nuclei absorb at different field strengths. In later sections we will be concerned with correlating the chemical shifts with structural features. However, before proceeding furher it is extremely important that you be able to identify the number and kind of nonequivalent protons in a given structure, and therefore the number of chemical shifts to expect. This number is not always self-evident, especially when subtle factors of stereochemistry intervene. For this reason, we suggest that you inspect structures \(3\)-\(5\) to convince yourself that the protons labeled with different letter subscripts in any one molecule are indeed chemically different.
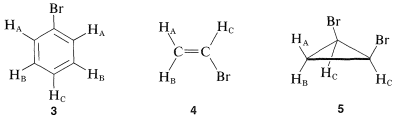
One way of checking whether two protons are in equivalent environments is to imagine that each is separately replaced with a different atom or group. If the product of replacing \(H_\text{A}\) is identical with that obtained by replacing \(H_\text{B}\), then \(H_\text{A}\) and \(H_\text{B}\) are chemically equivalent. If the two products are nonidentical, then \(H_\text{A}\) and \(H_\text{B}\) are nonequivalent. For example, replacement of \(H_\text{A}\) or \(H_\text{B}\) in \(3\), \(4\), and \(5\) by an atom \(X\) would give different products. Therefore, \(H_\text{A}\) and \(H_\text{B}\) are nonequivalent in \(3\), \(4\), and \(5\).
Matters become more complicated with substances such as \(6\) and \(7\):
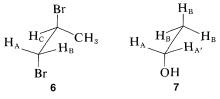
Notice that \(6\) represents a chiral molecule and if \(H_\text{A}\) and \(H_\text{B}\) each are replaced with \(X\) we get \(8\) and \(9\), which are diastereomers (see Section 5-5). You can verify this with molecular models if necessary. Diastereomers have different chemical and physical properties; therefore \(H_\text{A}\) and \(H_\text{B}\) in \(6\) are nonequivalent. They often are called diastereotopic hydrogens.
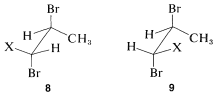
What of the two methylene protons in ethanol, \(7\), which we have labeled as \(H_\text{A}\) \(H_\text{A'}\)? Are they identical? In a sense they are not identical because, if each were replaced by \(X\), we would have a pair of enantiomers. Therefore, \(H_\text{A}\) and \(H_\text{A'}\) sometimes are called enantiotopic hydrogens.
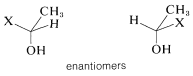
But, you will recall that enantiomers are chemically indistinguishable unless they are in a chiral environment. Therefore we expect shifts of enantiotopic hydrogens to be identical, unless they are in a chiral environment. To summarize, enantiotopic protons normally will have the same chemical shifts, whereas diastereotopic protons normally will have different chemical shifts.
We so far have ignored the relationship of chemical shifts to conformational equilibria. Consider a specific example, 1,2-dibromoethane, for which there are three staggered conformations \(10a\), \(10b\), and \(10c\):
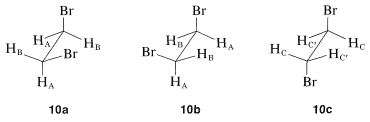
Each of these conformations is expected to have its own nmr spectrum. The two gauche forms, \(10a\) and \(10b\), are enantiomers and their spectra should be identical. The hydrogens \(H_\text{A}\) in \(10a\) each are trans to the bromine on the adjacent carbon, while the \(H_\text{B}\) hydrogens are cis to the same bromines (see Section 5-5A). Consequently the \(H_\text{A}\) and \(H_\text{B}\) hydrogens are nonequivalent and would be expected to have different chemical shifts. In contrast, all of the hydrogens of the anti conformer, \(10c\), are equivalent and would have the same chemical shift. Therefore we would expect to observe three chemical shifts arising from \(H_\text{A}\), \(H_\text{B}\), and \(H_\text{C}\) for a mixture of \(10a\), \(10b\), and \(10c\). However, the actual spectrum of 1,2-dibromoethane shows only one sharp proton signal under ordinary conditions. The reason is that the magnetic nuclei can absorb the exciting radiation. The result is that we observe an average chemical shift, which reflects the relative shifts and populations of the three conformers present. If we can go to a sufficiently low temperature to make interconversion of the conformations slow (on the order of 10 times per second), then we will expect to see the three different chemical shifts \(H_\text{A}\), \(H_\text{B}\), and \(H_\text{C}\) with intensities corresponding to the actual populations of the conformations at the sample temperature. This is one example of the effect of rate processes on nmr spectra. Other examples and a more detailed account of how to relate the appearance of the signal to the rates of the exchange processes are given in Section 27-2.
Chemical-Shift Standards and Units
Chemical shifts always are measured with reference to a standard. For protons or \(^{13}C\) in organic molecules, the customary standard is a tetramethylsilane, \(\left( CH_3 \right)_4 Si\), which gives strong, sharp nmr signals in regions where only a very few other kinds of protons or carbon nuclei absorb. Chemical shifts often are expressed in \(\text{Hz}\) (cycles per second) relative to tetramethylsilane (TMS). These may seem odd units for magnetic field strength but because resonance occurs at \(\nu = \gamma H\), either frequency units (\(\text{Hz}\), radians \(\text{sec}^{-1}\)) or magnetic field units (gauss) are appropriate.
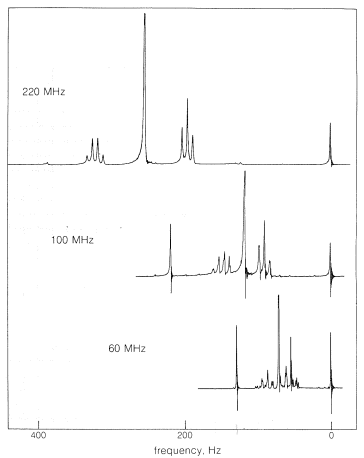
Ten years ago, most nmr spectrometers operated for protons with radio-frequency (rf) transmitters set at \(60 \: \text{MHz}\) (\(6 \times 10^7\) cycles per second) but there has been a proliferation of different proton-operating frequencies and now \(30\), \(60\), \(90\), \(100\), \(220\), \(270\), \(300\) and \(360 \: \text{MHz}\) machines are commercially available. The cost of these machines is roughly proportional to the square of the frequency, and one well may wonder why there is such an exotic variety available and what this has to do with the chemical shift. High operating frequencies are desirable because chemical shifts increase with spectrometer frequency, and this makes the spectra simpler to interpret. A 12-fold increase in operating frequency (as from \(30 \: \text{MHz}\) to \(360 \: \text{MHz}\)) means a 12-fold increase in \(H_\text{o}\) at the point of resonance (remember \(\nu = \gamma H\)) and this means also a 12-fold increase in \(\sigma H_\text{o}\). Thus resonances that differ because they correspond to different \(\sigma\) values will be twelve times farther apart at \(360 \: \text{MHz}\) than at \(30 \: \text{MHz}\). This can produce a dramatic simplification of spectra, as can be seen from Figure 9-27, which shows the effect of almost a factor of four in \(\nu\) on the proton nmr spectrum of 2-methyl-2-butanol.\(^{12}\)
To reiterate, chemical shifts are strictly proportional to spectrometer frequency, thus lines \(100 \: \text{Hz}\) apart at \(60 \: \text{MHz}\) will be \(167 \: \text{Hz}\) apart at \(100 \: \text{MHz}\). This might seem to make comparisons of nmr spectra on different spectrometers hopelessly complex but, because of the proportionality of shifts to frequency (or field), if we divide the measured shifts in \(\text{Hz}\) (relative to the same standard) for any spectrometer by the transmitter frequency in \(\text{MHz}\), we get a set of frequency-independent shifts in parts per million (\(\text{ppm}\), which are useful for all nmr spectrometers. Nmr shifts reported in \(\text{ppm}\) relative to TMS as zero, as shown in Figure 9-23, are called \(\delta\) (delta) values:
\[\delta = \frac{\left( \text{chemical shift downfield in Hz relative to TMS} \right) \times 10^6}{\text{spectrometer frequency in Hz}}\]
Thus, if at \(60 \: \text{MHz}\) a proton signal comes \(100 \: \text{Hz}\) downfield relative to tetramethylsilane, it can be designated as being \(\left( +100 \: \text{Hz} \times 10^6 \right)/ 60 \times 10^6 \: \text{Hz} = +1.67 : \text{ppm}\) relative to tetramethylsilane. At \(100 \: \text{MHz}\), the line then will be \(\left( 1.67 \times 10^{-6} \right) \left(100 \times 10^6 \right) = 167 \: \text{Hz}\) downfield from tetramethylsilane. Typical proton chemical shifts relative to TMS are given in Table 9-4.\(^{13}\) The values quoted for each type of proton may, in practice, show variations of \(0.1\)-\(0.3 \: \text{ppm}\). This is not unreasonable, because the chemical shift of a given proton is expected to depend somewhat on the nature of the particular molecule involved, and also on the solvent, temperature, and concentration.
A positive \(\delta\) value means a shift to lower field (or lower frequency) with respect to TMS, whereas a negative \(\delta\) signifies a shift to higher field (or higher frequency). The \(\delta\) convention is accepted widely, but you often find in the literature proton shifts with reference to TMS reported as "\(\tau\) values." The \(\tau\) scale has the TMS reference at \(+10 \: \text{ppm}\), so most proton signals fall in the range of \(\tau = 0\) to \(\tau = +10\). A \(\tau\) value can be converted to the appropriate \(\delta\) value by subtracting it from 10. Life with nmr spectra would be simpler if the \(\tau\) scale would just go away.
Correlations Between Structure and Chemical Shifts
Protonc chemical shifts are very valuable for the determination of structures, but to use the shifts in this way we must know something about the correlations that exist between chemical shift and structural environment of protons in organic compounds. The most important effects arise from differences in electronegativity, types of carbon bonding, hydrogen bonding, and chemical exchange.
Electronegativity
Consider first the chemical shifts of protons attached to an \(sp^3\) carbon, 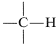 .
.
The degree of shielding of the proton by the carbon valence electrons depends on the character of the substituent atoms and groups present, and particularly on their electron-attracting power, or electronegativity. For a grouping of the type 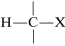 , the shielding will be less as \(\ce{X}\) is more electron withdrawing relative to hydrogen:
, the shielding will be less as \(\ce{X}\) is more electron withdrawing relative to hydrogen:
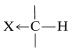 If \(\ce{X}\) is electron-withdrawing, the proton is deshielded.
If \(\ce{X}\) is electron-withdrawing, the proton is deshielded.
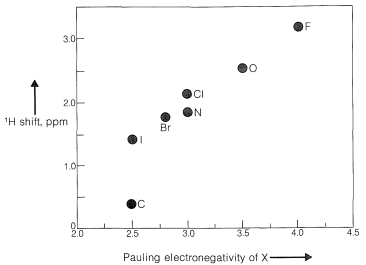
For example, the proton chemical shifts of the methyl halides (Table 9-4) show decreasing shielding, hence progressively low-field chemical shifts with increasing halogen electronegativity \(\left( \ce{F} > \ce{Cl} > \ce{Br} > \ce{I} \right)\):
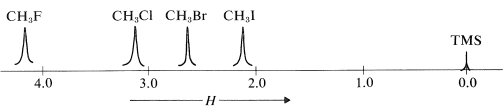
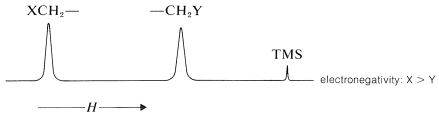
Table 9-4: Typical Proton Chemical-Shift Values \(\left( \delta \right)\) in Dilute \(\ce{CHCl_3}\) Solutions

When two electronegative groups, \(\ce{X}\) and \(\ce{Y}\), are bonded to the same carbon, as in \(\ce{XCH_2Y}\), the protons are expected to be less shielded and come into resonance downfield of the methylenes of \(\ce{XCH_2CH_2Y}\). There is an approximate relationship (see below) between the shifts of the \(\ce{XCH_2Y}\) protons and the effective shielding constants \(\left( \sigma \right)\) of \(\ce{X}\) and \(\ce{Y}\) known as Shoolery's rule.
\[\delta = 0.23 + \sigma_x + \sigma_y \tag{9-4}\]
Appropriate values of \(\sigma\) for use with this equation are given in Table 9-4.
Effects of Carbon Bond Type
The shifts of the protons of alkanes and cycloalkanes fall in the range of \(0.9\)-\(1.5 \: \text{ppm}\) with \(\ce{C-H}\) protons coming at the low-field end of this range and \(\ce{-CH_3}\) protons coming at the high-field end (see Table 9-4).
Alkenic hydrogens (vinyl hydrogens,  ) normally are observed between \(4.6\)-\(6.3 \: \text{ppm}\) toward lower fields than the shifts of protons in alkanes and cycloalkanes. This means that alkenic hydrogens in an organic compound can be easily distinguished from alkane hydrogens.
) normally are observed between \(4.6\)-\(6.3 \: \text{ppm}\) toward lower fields than the shifts of protons in alkanes and cycloalkanes. This means that alkenic hydrogens in an organic compound can be easily distinguished from alkane hydrogens.
Aromatic protons, such as those in benzene, have shifts at still lower fields and commonly are observed at \(7\)-\(8 \: \text{ppm}\). In contrast, alkynic protons of the type \(\ce{-C \equiv CH}\) give resonances that are upfield of alkenic or aromatic protons and come at \(2\)-\(3 \: \text{ppm}\). Another effect associated with multiple bonds is the large difference in shift between a \(\ce{-CH(OCH_3)_2}\) proton, which normally comes at about \(5.5 \: \text{ppm}\), and aldehyde protons, \(\ce{-CH=O}\), which are much farter downfield at \(9\)-\(11 \: \text{ppm}\).
Clearly, the shifts of a proton depend on whether the carbon forms single, double, or triple bonds. In a magnetic field, the circulation of electrons in the \(\pi\) orbitals of multiple bonds induced by the field (Figure 9-26) generates diamagnetic shielding effects in some regions of the multiple bond and paramagnetic deshielding effects in other regions. Apparently, protons attached to double-bonded carbons are in the deshielding zones and thus are downfield while protons attached to triple-bonded carbons are in the shielding zones and are observed at rather high field.
Hydrogen Bonding
When a proton is directly bonded to a strongly electronegative atom such as oxygen or nitrogen its chemical shift is critically dependent on the nature of the solvent, temperature, concentration, and whether acidic or basic impurities are present. The usual variations in chemical shift for such protons are so large (up to \(5 \: \text{ppm}\) for alcohols) that no very useful correlations exist.
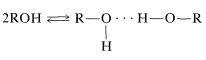
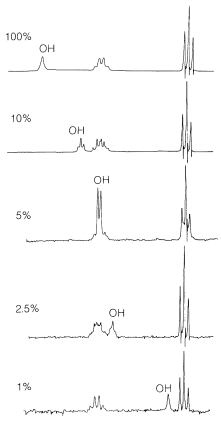
Hydrogen bonding is the major reason for the variable chemical shifts of \(\ce{OH}\) and \(\ce{NH}\) protons. In general, hydrogen bonding results in deshielding, which causes the resonances to move downfield. The extent of hydrogen bonding varies with concentration, temperature, and solvent, and changes in the degree of hydrogen bonding can cause substantial shift changes. This is very evident in the nmr spectrum of ethanol taken at different concentrations in \(\ce{CCl_4}\) (Figure 9-29). The hydroxyl resonance will be seen to move upfield by hydrogen bonding through equilibria such as
Chemical Exchange
Many \(\ce{OH}\) and \(\ce{NH}\) compounds are weak acids and weak bases and can undergo autoprotolysis, which means that a proton can be transferred from one molecule to another. Suppose we have a compound such as 2-aminoethanol, \(\ce{H_2NCH_2CH_2OH}\). This substance normally would be expected to have an \(\ce{NH_2}\) proton resonance at about \(1 \: \text{ppm}\) and an \(\ce{OH}\) proton resonance at about \(3 \: \text{ppm}\). Autoprotolysis equilibria can exchange the protons between the molecules and also from one end to the other as shown below, even if the equilibria are not very favorable.
\[\begin{align} \ce{NH_2CH_2CH_2OH} &\overset{\rightarrow}{\longleftarrow} ^\oplus \ce{NH_3CH_2CH_2O}^\ominus \tag{9-5} \\ 2 \ce{NH_2CH_2CH_2OH} &\overset{\rightarrow}{\longleftarrow} ^\oplus \ce{NH_3CH_2CH_2OH} + \ce{N_2CH_2CH_2O}^\ominus \tag{9-6} \end{align}\]
Such equilibria can be established very rapidly, especially if traces of a strong acid or a strong base are present. In such circumstances, a single average \(\left( \ce{-NH_2}, \: \ce{-OH} \right)\) proton signal is observed, because the excitation of a given proton from its lower-energy magnetic state to its higher-energy magnetic state occurs while it is partly on oxygen and partly on nitrogen. This is the same kind of chemical shift averaging that occurs for rapidly equilibrating conformations (see Section 9-10C).
Application of Chemical Shifts to Structure Determination
To see how nmr and infrared spectra can be used together for structure determination we shall work through a representative example.
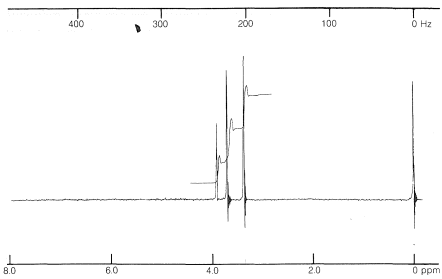
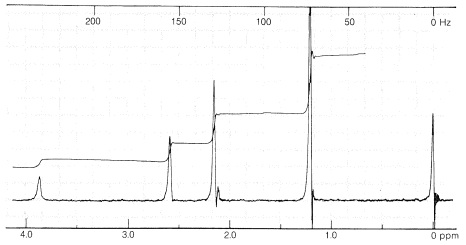
The objective is to assign a structure to the compound \(\ce{C_4H_8O_3}\) whose nmr spectrum is shown in Figure 9-30 and whose infrared spectrum shows prominent bands at \(2900 \: \text{cm}^{-1}\), \(1750 \: \text{cm}^{-1}\), \(1000 \: \text{cm}^{-1}\), and \(1100 \: \text{cm}^{-1}\).
The infrared spectrum indicates 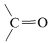 \(\left( 1750 \: \text{cm}^{-1} \right)\), \(\ce{C-H} \: \left( 2900 \: \text{cm}^{-1} \right)\), and \(\ce{C-O} \: \left( 1000 \: \text{cm}^{-1}, \: 1100 \: \text{cm}^{-1} \right)\). The position of the carbonyl band suggests that it is probably an ester,
\(\left( 1750 \: \text{cm}^{-1} \right)\), \(\ce{C-H} \: \left( 2900 \: \text{cm}^{-1} \right)\), and \(\ce{C-O} \: \left( 1000 \: \text{cm}^{-1}, \: 1100 \: \text{cm}^{-1} \right)\). The position of the carbonyl band suggests that it is probably an ester, 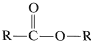 . A carboxylic acid is ruled out because there is no sign of an \(\ce{O-H}\) stretch.
. A carboxylic acid is ruled out because there is no sign of an \(\ce{O-H}\) stretch.
The nmr spectrum shows three kinds of signals corresponding to three kinds of protons. The integral shows these are in the ratio of 2:3:3. From this, we can conclude that they are two different kinds of \(\ce{CH_3-}\) groups and a \(\ce{-CH_2-}\) group.
The chemical shifts of the presumed \(\ce{CH_3}\) groups are at \(3.70 \: \text{ppm}\) and \(3.35 \: \text{ppm}\). Because the compound contains only \(\ce{C}\), \(\ce{H}\), and \(\ce{O}\), the data of Table 9-4 suggest that these resonances arise from \(\ce{OCH_3}\) groups. The low-field resonance is likely to be 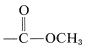 (we know from the infrared that there probably is an ester function), while the higher-field resonance is possibly an ether function, \(\ce{-OCH_3}\). If you put all of this information together, you find that \(\ce{CH_3OCH_2CO_2CH_3}\) is the only possible structure. To check whether the \(\ce{CH_2}\) resonance at \(3.9 \: \text{ppm}\) is consistent with the assigned structure we can calculate a shift value from Equation 9-4:
(we know from the infrared that there probably is an ester function), while the higher-field resonance is possibly an ether function, \(\ce{-OCH_3}\). If you put all of this information together, you find that \(\ce{CH_3OCH_2CO_2CH_3}\) is the only possible structure. To check whether the \(\ce{CH_2}\) resonance at \(3.9 \: \text{ppm}\) is consistent with the assigned structure we can calculate a shift value from Equation 9-4:
\[\begin{align} &\delta = 0.23 + \sigma_{OCH_3} + \sigma_{O=COCH_3} \\ &\delta = 0.23 + 2.36 + 1.55 = 4.14 \: \text{ppm} \end{align}\]
The agreement between the calculated and observed shifts is not perfect, but is within the usual range of variation for Equation 9-4. We can be satisfied that the assigned structure is correct.
Spin-Spin Splitting - What We Observe
If you look at the nmr spectrum of ethanol, \(\ce{CH_3CH_2OH}\), in Figure 9-23, you will see that the \(\ce{CH_2}\) resonance is actually a group of four lines and the \(\ce{CH_3}\) resonance is a group of three lines. This three-four line pattern for the grouping \(\ce{CH_3CH_2X} \: \left( \ce{X} \neq \ce{H} \right)\) also is evident in the \(220 \: \text{MHz}\) spectrum of 2-methyl-2-butanol (Figure 9-27) and in the \(60 \: \text{MHz}\) spectrum of ethyl iodide (Figure 9-32).
Why do certain proton resonances appear as groups of equally spaced lines rather than single resonances? The facts are that nonequivalent protons on contiguous carbons  , such as ethyl derivatives \(\ce{CH_3CH_2X}\), interact magnetically to "split" each other's resonances. This multiplicity of lines produced by the mutual interaction of magnetic nuclei is called "spin-spin splitting", and while it complicates nmr spectra, it also provides valuable structural information, as we shall see.
, such as ethyl derivatives \(\ce{CH_3CH_2X}\), interact magnetically to "split" each other's resonances. This multiplicity of lines produced by the mutual interaction of magnetic nuclei is called "spin-spin splitting", and while it complicates nmr spectra, it also provides valuable structural information, as we shall see.
An example of a complex proton spectrum is that of ethyl iodide (Figure 9-32). To a first approximation, the two main groups of lines appear as equally spaced sets of three and four lines, arising from what are called "first-order spin-spin interactions". Matters are further complicated by additional splitting of the "three-four" pattern of ethyl iodide, as also can be seen in Figure 9-32. This additional splitting is called "second-order" splitting.
When there are so many lines present, how do we know what we are dealing with? From where to we measure the chemical shift in a complex group of lines?
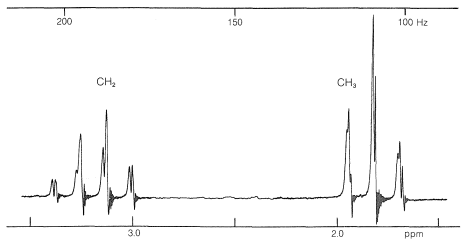
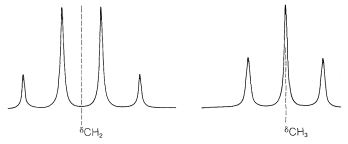
First, the chemical shift normally is at the center of the group of lines corresponding to first-order splitting. In ethyl iodide, the chemical shift of the methyl protons is in the center of the quartet:
Second, the chemical shift can be recognized by the fact that it is directly proportional to the transmitter frequency, \(\nu\). If we double \(\nu\), the chemical shifts double. In contrast, the first-order spin-spin splittings remain the same. By this we mean that the magnitude (in \(\text{Hz}\)) of the spacing between the lines of a split resonance is independent of the transmitter frequency, \(\nu\). This spacing corresponds to what is called the spin-spin coupling constant, or simply the coupling constant, and is symbolized by \(J\).
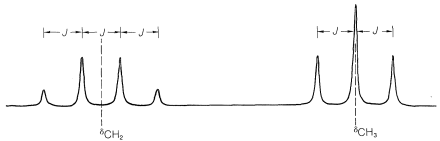
Third, the second-order splitting tends to disappear with increasing transmitter frequency. For ethyl iodide (Figure 9-32), the second-order splitting at \(60 \: \text{MHz}\) is barely discernible at \(100 \: \text{MHz}\) and disappears at \(200 \: \text{MHz}\). This also can be seen to occur for the three-four splitting pattern of 2-methyl-2-butanol as a function of \(\nu\) (Figure 9-27).
The next question is how can we understand and predict what spin-spin splitting patterns will be observed? And how do they give us structural information? The important point is that the multiplicity of lines for protons of a given chemical shift often is seen to be \(\left( n + 1 \right)\), in which \(n\) is the number of protons on the contiguous carbons. For example, the \(\ce{CH_2}\) resonance of the ethyl group of ethyl iodide is a quartet of lines because of the spin-spin interaction with the neighboring three protons \(\left( n = 3 \right)\) of the methyl group. Likewise, the \(\ce{CH_3}\) group is a triplet of lines because of spin-spin interactions with the two protons \(\left( n = 2 \right)\) of the methylene group.
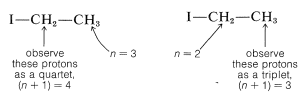
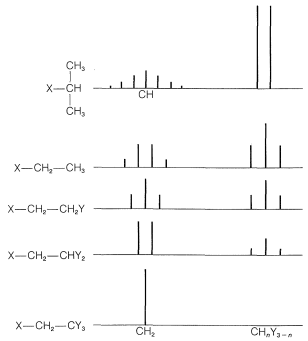
The ratios of the line intensities in the spin-spin splitting patterns of Figure 9-33 usually follow simple rules. A doublet appears as two lines of equal intensity; a triplet as three lines in the ratio 1:2:1; a quartet as four lines in the ratio 1:3:3:1; a quintet as 1:4:6:4:1, and so on. The intensities follow the binomial coefficients for \(\left( x + y \right)^n\), where \(n\) is the number of protons in the splitting group. Thus when \(n = 4\), we have \(x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4\), or 1:4:6:4:1.
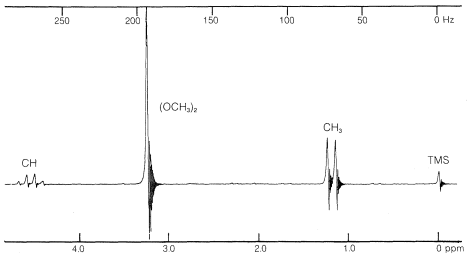
The spectrum of \(\ce{(CH_3O)_2CHCH_3}\) (Figure 9-34) provides an excellent example of how nmr shows the presence of contiguous protons. The symmetrical doublet and 1:3:3:1 quartet are typical of the interaction between a single proton and an adjacent group of three, that is, 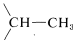 . The methyl protons of the \(\ce{(CH_3O)}\) groups are too far from the others to give demonstrable spin-spin splitting; thus they appear as a single six-proton resonance.
. The methyl protons of the \(\ce{(CH_3O)}\) groups are too far from the others to give demonstrable spin-spin splitting; thus they appear as a single six-proton resonance.
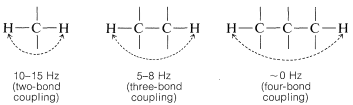
In general, the magnitude of the spin-spin splitting effect of one proton on another proton (or group of equivalent protons) depends on the number and kind of intervening chemical bonds and on the spatial relationships between the groups. For simple systems without double bonds and with normal bond angles, we usually find for nonequivalent protons (i.e., having different chemical shifts):
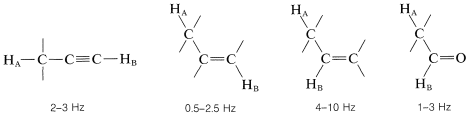
Where restricted rotation or double- and triple-bonded groups are involved, widely divergent splittings are observed. For double bonds, the two-bond couplings between two nonequivalent hydrogens located on one end are characteristically small, while the three-bond couplings in \(\ce{-HC=CH}-\) are larger, especially for the trans configuration:

Coupling through four or more bonds is significant for compounds with double or triple bonds. Examples of these so-called long-range couplings and some other useful splitting values follow:
Finally, chemically equivalent protons do not split each other's resonances.
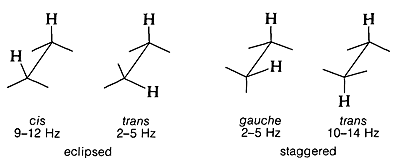
Proton-Proton Splittings and Conformational Analysis
A very important characteristic of three-bond proton-proton couplings, \(\ce{H-C-C-H}\), is the way that they depend on the conformation at the \(\ce{C-C}\) bond. Typical values for several particular conformations are
Proton-Proton Splittings and Chemical Exchange
You may have wondered why the hydroxyl proton of ethanol produces a single resonance in the spectrum of Figure 9-23. It is quite reasonable to expect that the hydroxyl proton would be split by the neighboring methylene protons because they are only three bonds apart,  however, this coupling will not be observed if the hydroxyl protons are exchanging rapidly between the ethanol molecules (Section 9-10E). When proton exchange is rapid, the spin interactions between the \(\ce{-CH_2}-\) and \(\ce{-OH}\) protons average to zero. At intermediate exchange rates, the coupling manifests itself through line broadening or by actually giving multiple lines. If you look at the several spectra of ethanol in Figure 9-29, you will notice how the shape of the \(\ce{OH}\) resonance varies from a broad singlet to a distinct triplet.
however, this coupling will not be observed if the hydroxyl protons are exchanging rapidly between the ethanol molecules (Section 9-10E). When proton exchange is rapid, the spin interactions between the \(\ce{-CH_2}-\) and \(\ce{-OH}\) protons average to zero. At intermediate exchange rates, the coupling manifests itself through line broadening or by actually giving multiple lines. If you look at the several spectra of ethanol in Figure 9-29, you will notice how the shape of the \(\ce{OH}\) resonance varies from a broad singlet to a distinct triplet.
Rapid chemical exchange of magnetic nuclei is not the only way that spin-coupling interactions can be averaged to zero. The same effect can be achieved by a technique known as double resonance. To understand how this is done, consider two coupled protons \(\ce{H}_\text{A}\) and \(\ce{H}_\text{B}\) having different chemical shifts. Suppose that \(\ce{H}_\text{A}\) is selectively irradiated at its resonance frequency \(\nu_\text{A}\) while at the same time we observe the resonance signal of \(\ce{H}_\text{B}\). The coupling between \(\ce{H}_\text{A}\) and \(\ce{H}_\text{B}\) disappears, and \(\ce{H}_\text{B}\) shows a single resonance. Why is this so? By irradiation of \(\ce{H}_\text{A}\), the \(\ce{H}_\text{A}\) nuclei are changed from the +1/2 state to -1/2 and back again sufficiently rapidly that the neighboring nucleus \(\ce{H}_\text{B}\) effectively “sees” neither one state nor the other. The magnetic interaction between the states therefore averages to zero. This decoupling of magnetic nuclei by double resonance techniques is especially important in \(\ce{^{13}C}\) NMR spectroscopy (Section 9-10L) but also is used to simplify proton spectra by selectively removing particular couplings.
Use of Nuclear Magnetic Resonance Spectroscopy in Organic Structural Analysis
The solution of a typical structural analysis problem by nmr methods utilizes at least four kinds of information obtained directly from the spectrum. They are: chemical shifts \(\left( \delta \right)\), line intensities (signal areas), spin-spin splitting patterns (line mulitplicities), and coupling constants \(\left( J \right)\). We already have shown how chemical shifts are used in the absence of spin-spin splitting. We now will illustrate how more complex spectra may be analyzed.
Figure 9-35 shows the proton nmr spectrum for a compound of formula \(\ce{C_3H_6O}\). There are three principal groups of lines at \(9.8\), \(2.4\), and \(1.0 \: \text{ppm}\). Look at the multiplicity of these groups before reading further.
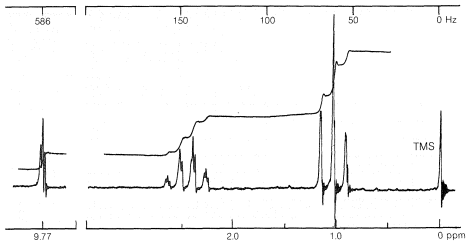
There are several ways to approach a problem such as this, but probably the easiest is to start with the integral. The relative heights of the stepped integral for the principal groups of lines can be obtained by a pair of dividers, with a ruler, or with horizontal lines as in Figure 9-35. The integral suggests that one hydrogen is responsible for the resonance at \(9.8 \: \text{ppm}\), two hydrogens at \(2.4 \: \text{ppm}\), and three at \(1.0 \: \text{ppm}\). Three hydrogens in a single group suggest a \(\ce{CH_3}-\) group, and because there is a three-four splitting pattern, it is reasonable to postulate \(\ce{CH_3-CH_2}-\). Subtracting \(\ce{C_2H_5}\) from the given formula \(\ce{C_3H_6O}\) leaves \(\ce{CHO}\), which, with normal valences, has to be \(\ce{-CH=O}\). The spectrum thus appears to be consistent with the structure \(\ce{CH_3CH_2CH=O}\) (propanal) as judged from the molecular formula and the spin-spin splitting pattern, which indicates the \(\ce{CH_3CH_2}-\) grouping. To be sure of the structure, we should check it against all of the available information. First, from the shifts (Table 9-4) we see that the single proton at \(9.8 \: \text{ppm}\) fits almost perfectly for \(\ce{RCHO}\), the two-proton \(\ce{-CH_2C=O}\) resonance at \(2.4 \: \text{ppm}\) is consistent with that reported for \(\ce{-CH_2COR}\), while the three-proton line at \(1.0 \: \text{ppm}\) checks with \(0.9 \: \text{ppm}\) for \(\ce{CH_3R}\).
What about the couplings? The three-four pattern has a spacing of slightly over \(7 \: \text{Hz}\), which is just right for an ethyl group (compare Figures 9-23 and 9-32). The doubling up (almost obscured by second-order splitting) of the \(\ce{-CH_2}-\) resonance and the splitting of the \(\ce{-CH=O}\) resonance into a 1:2:1 triplet indicate about a \(2\)-\(\text{Hz}\) coupling for the \(\ce{-CH_2-CH=O}\) group. Three-bond couplings between \(\ce{-CHO}\) and adjacent \(\ce{-CH_2}-\) protons appear to be generally smaller than \(\ce{-CH_2-CH_3}\) couplings.
We usually would not rely on nmr alone in a structure-analysis problem of this kind, but would seek clues or corroboration from the infrared, electronic, or other spectra, as well as chemical tests. In later chapters we will have many problems that will be facilitated by the use of both nmr and infrared spectra. A further worked example will illustrate the approach.
A compound has the composition \(\ce{C_3H_3Br}\) and gives the infrared and nuclear magnetic resonance spectra shown in Figure 9-36. The problem is how to use this information to deduce the structure of the compound. The molecular formula tells us the number and kind of atoms and the number of multiple bonds or rings. The formulas of the corresponding \(\ce{C_3}\) hydrocarbon without the bromine would be \(\ce{C_3H_4}\), or four hydrogens less than the saturated alkane \(\ce{C_3H_8}\). This means there must be two double bonds or the equivalent - one triple bond or one ring and one double bond.\(^{14}\) Because from the formula we suspect unsaturation, we should check this out with the infrared spectrum. There is a band at \(2120 \: \text{cm}^{-1}\), which is indicative of an unsymmetrically substituted \(\ce{-C \equiv C}-\) group (Table 9-2). The strong, sharp band at \(3300 \: \text{cm}^{-1}\) further tells us that the substance is a 1-alkyne \(\ce{-C \equiv C-H}\).
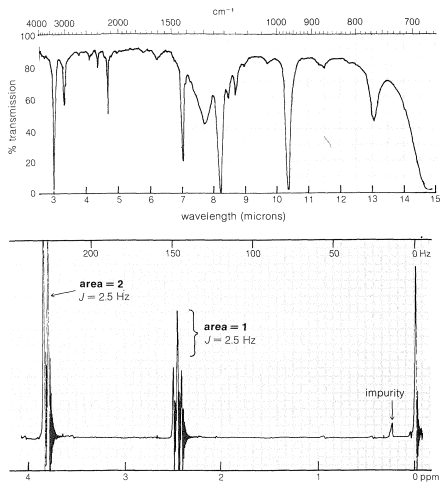
The proton nmr spectrum shows that there are only two principal groups of lines - a two-proton doublet at \(3.85 \: \text{ppm}\) and a one-proton triplet at \(2.45 \: \text{ppm}\). The two-three splitting pattern combined with the 2:1 proton ratio suggests a \(\ce{CH_2}\) group coupled with a \(\ce{CH}\) group. The structure must be a 3-bromo-propyne, \(\ce{BrCH_2C \equiv CH}\). To confirm the assignment, the chemical shifts should be checked (Table 9-4). The \(\ce{\equiv C-H}\) at \(2.45 \: \text{ppm}\) agrees well with the tabulated value of \(2.5 \: \text{ppm}\). There is no tabulated data for \(\ce{-C \equiv C-CH_2Br}\) but the observed shift at \(3.85 \: \text{ppm}\) is at slightly lower fields than the tabulated \(3.33 \: \text{ppm}\) for \(\ce{-CH_2Br}\). This is expected because of the triple bond. The correlation of Equation 9-4 predicts a value of \(4.0 \: \text{ppm}\).
Very often, a proton will be spin-coupled to two or more different protons, and the couplings are not necessarily the same. When this happens, the resulting spectrum can be quite complex, as our next example shows.
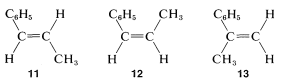
A compound \(\ce{C_9H_{10}}\) gives the nmr spectrum of Figure 9-37. There are clearly four kinds of protons in the molecule at \(\delta = 7.28 \: \text{ppm}\), \(5.35 \: \text{ppm}\), \(5.11 \: \text{ppm}\), and \(1.81 \: \text{ppm}\). Although the integral is not shown, the main groups of lines have intensities from the low-field to high-field in the ratio of 5:1:1:3.
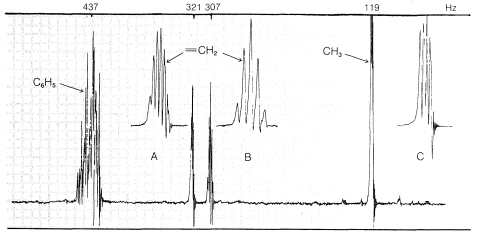
The five-proton signal at \(7.28 \: \text{ppm}\) is typical of a phenyl group, \(\ce{C_6H_5}\), and the one-proton signals at \(5.35\) and \(5.11 \: \text{ppm}\) are in the region for alkenic protons, 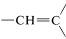 . The three-proton signal at \(1.81 \: \text{ppm}\) is typical of a methyl group on a carbon-carbon double bond,
. The three-proton signal at \(1.81 \: \text{ppm}\) is typical of a methyl group on a carbon-carbon double bond, 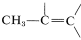 .
.
There are only three ways to put together a phenyl ring,  , and two \(\ce{HC=}\) protons such that they add up to \(\ce{C_9H_{10}}\). They are
, and two \(\ce{HC=}\) protons such that they add up to \(\ce{C_9H_{10}}\). They are
Coupling between A and B (designated by the constant \(J_\text{AB}\)) should give four lines, two for A and two for B, as shown in Figure 9-38. Because A and B also are coupled to the three hydrogens of the methyl group (C), each of the four lines corresponding to \(J_\text{AB}\) will be further split (into 1:3:3:1 quartets). If \(J_\text{AC} \neq J_\text{BC}\), then the spacing of the lines in the two sets of quartets will not be the same.
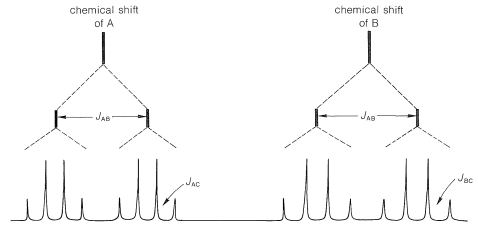
 where \(J_\text{AB} \gg J_\text{B} > J_\text{AC}\).
where \(J_\text{AB} \gg J_\text{B} > J_\text{AC}\).According to the foregoing analysis, the maximum number of lines observable for the A and B resonances is sixteen (8 for A and 8 for B). In fact, only eleven are visible (6 for A and 5 for B), which means that some of the sixteen possible lines must overlap. Without examining all possibilities, we can see that the actual situation can be reproduced if \(J_\text{AB} \cong J_\text{BC} = 2J_\text{AC}\). The only structure that is consistent with \(J_\text{AB} = 1.5 \: \text{Hz}\) is \(13\), or 2-phenylpropene; the other possibilities are excluded because \(J_\text{AB}\) should be about \(10 \: \text{Hz}\) for \(12\) and \(16 \: \text{Hz}\) for \(11\).
Chemical-Shift Effects on Spin-Spin Splitting
The simple \(n + 1\) rule for predicting the multiplicity of spin-coupled proton signals often breaks down whenever the chemical-shift difference between the protons in different groups becomes comparable to coupling constants for magnetic interaction between the groups. Under these circumstances, you may expect to see more lines, or lines in different positions with different intensities, than predicted from the simple first-order treatment. One example is the effect of changing chemical shift on a two-proton spectrum with \(J = 10 \: \text{Hz}\) (Figure 9-44).
We see in Figure 9-44 that even when the shift is 7.5 times larger than the coupling, the outside lines are weaker than the inside lines. This general kind of asymmetry of line intensities also is apparent in the spectrum of ethyl iodide (Figure 9-32), in which the lines of each group are more like 0.7:2.5:3.5:1.3 and 1.2:2.0:0.8, rather than the 1:3:3:1 and 1:2:1 ratios predicted from the first-order treatment. The asymmetry is such that two groups of lines that are connected by spin-spin splitting in effect "point" to one another - the lines on the "inside" of the pattern are stronger than predicted from the first-order treatment, whereas those on the "outside" are weaker. The effect can be put to practical use, as illustrated in the following exercise.
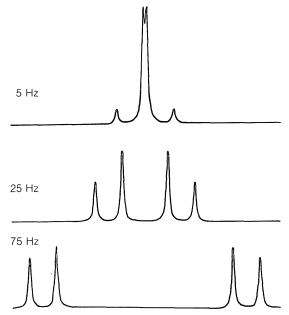
To explain the effect of chemical shifts on second-order splitting is beyond the scope of this book. In fact, we haven't really explained first-order splitting, although more on this topic will be found in Section 27-3. But regardless of how many lines appear in a complex nmr spectrum, they can be rationalized in terms of the chemical shifts, coupling constants, and exchange effects. Furthermore, the overall signal intensities remain proportional to the number of protons giving rise to the signals.
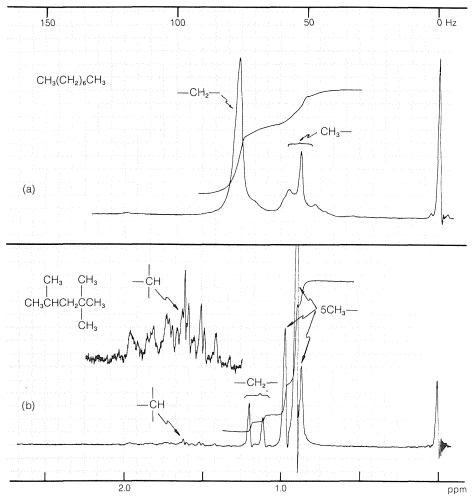
When there are many hydrogens and small chemical-shift differences, as in alkanes, the proton nmr spectra may have so many closely spaced resonance lines that they merge together to give a series of smooth, more-or-less featureless peaks. The proton spectrum of octane (Figure 9-46a) is an excellent example of this type of spectrum. Useful information often can be obtained from such spectra as to the ratio of \(\ce{CH_3}\) : \(\ce{CH_2}\) : \(\ce{CH}\) by investigation of the integrals over the range of alkane proton absorptions. Figure 9-46 illustrates how this can be done for octane and 2,2,4-trimethylpentane.
Carbon-13 Nuclear Magnetic Resonance Spectroscopy
In recent years \(\ce{^{13}C}\) nmr spectroscopy using \(\ce{^{13}C}\) of natural abundance \(\left( 1.1 \% \right)\) has become an important tool for organic structural analysis. That this did not happen sooner is because \(\ce{^{13}C}\) has a much smaller magnetic moment than \(\ce{^1H}\) and the small moment combined with the small natural abundance means that \(\ce{^{13}C}\) is harder to detect in the nmr than \(\ce{^1H}\) by a factor of 5700. This is a large difference and can be put in the proper context in the following way. Suppose two people are talking in a noisy room and one is trying to hear the other. The common request is "talk louder". If this is not possible then the request is "say it again" or "talk more slowly". Either of the latter requests amounts to an integration of signal versus noise and takes time. Improvement in signal-to-noise for a given communication is achieved as the square root of the time of communication. On the crucial time basis, \(\ce{^{13}C}\) nmr signals require \(\left( 5700 \right)^2 \cong 30,000,000\) times more time to get the same signal-to-noise ratio as in \(\ce{^1H}\) nmr for the same number of nuclei per unit volume. This is a problem.
Electronic improvements and use of communication theory, with emphasis on the "say-it-again" technique, have provided the means for obtaining routine \(\ce{^{13}C}\) spectra for even fairly dilute solutions of quite complex molecules.
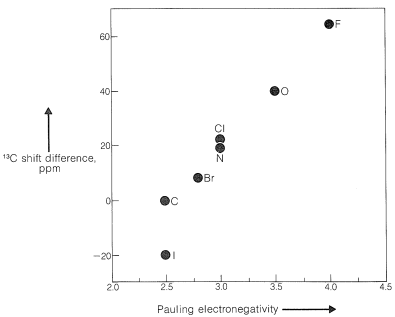
Some of the same kinds of structural effects are important for \(\ce{^{13}C}\) chemical shifts as for proton chemical shifts (Section 9-10E). For example, there is a similar parallel between \(\ce{^{13}C}\) shift differences in compounds of the type \(\ce{CH_3-CH_2-X}\) and electronegativity (Figure 9-47) as between the corresponding proton shifts and electronegativity (Figure 9-28). It is important to notice that \(\ce{^{13}C}\) shifts in \(\text{ppm}\) units are much larger than those of protons. This is because carbon uses \(p\) orbitals in forming bonds, whereas hydrogen uses \(s\) orbitals. We therefore will expect to find the the nuclei of other elements that use \(p\) orbitals in bonding, such as \(\ce{^{15}N}\), \(\ce{^{19}F}\), and \(\ce{^{31}P}\), also will have larger shifts than for protons, as indeed they do.
A structural application of \(\ce{^{13}C}\) nmr, which shows its power in an area where \(\ce{^1H}\) nmr is indecisive, is shown in Figure 9-48. Here, we see the high-field \(\ce{^{13}C}\) resonances of a substance known variously as Coumadin, or the sodium salt of warfarin, \(14\), which is used widely as a blood anticoagulant in the treatment of diseases such as phlebitis. It also has substantial utility as a rat poison because of its anticoagulant action.
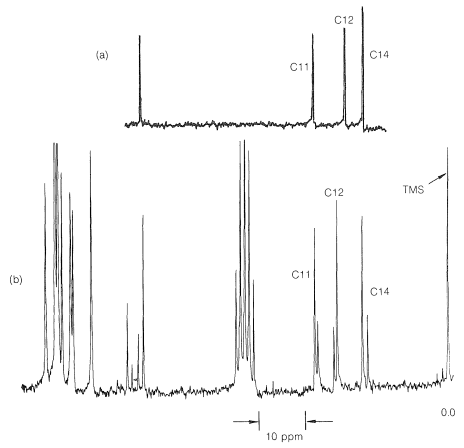
There is no indication of any abnormality in the chemical shifts of carbons 11, 12, and 14 shown in Figure 9-48a. Furthermore, there is a downfield resonance \(216.5 \: \text{ppm}\) from the carbons of TMS (not shown in Figure 9-48a) which is typical of a \(\ce{C=O}\) carbon corresponding to C13. When \(14\) is treated with acid, we expect the product (warfarin) of structure \(15\) to be formed, which should have a \(\ce{^{13}C}\) spectrum much like that shown in Figure 9-48a.
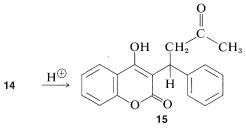
The \(\ce{^{13}C}\) data indicate clearly that warfarin is not \(15\) in solution but is a mixture of two diastereomers (\(16\) and \(17\), called cyclic hemiketals) resulting from addition of the \(\ce{-OH}\) group of \(15\) to the \(\ce{C=O}\) bond:
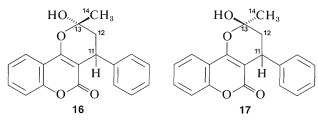
This is one example of the power of \(\ce{^{13}C}\) nmr to solve subtle structural problems.
\(^8\)Although the principal isotopes of \(Cl\), \(Br\), and \(I\) have magnetic properties, because of the special character of all of these isotopes, they act in organic compounds as though they were nonmagnetic.
\(^9\)Resonance in the sense used here means that the radio-frequency absorption takes place at specified "resonance" frequencies. However, you will see that almost all of the forms of spectroscopy we discuss in this book involve "resonance" absorption in the same sense.
\(^{10}\)Here, \(\gamma\) is in \(\text{Hz}\) per gauss; physicists usually define \(\gamma\) in radians per second per gauss.
\(^{11}\)From the Greek prefix dia meaning through, across. The opposite of diamagnetic is paramagnetic; para meaning alongside. We shall use this term later.
\(^{12}\)In addition to giving better separation of the lines and clearer spectra, going to higher fields also has the beneficial effect of increasing the proportions of the nuclei in the \(+ \frac{1}{2}\) state, thereby giving more intense, easier-to-detect resonances.
\(^{13}\)Many other proton-shift values are available in NMR Spectra Catalog, Volume 1 and 2, Varian Associates, Palo Alto, Calif., 1962, 1963.
\(^{14}\)If two rings were present, this also would give four hydrogens less than the alkane. However, two rings are not possible with only three carbons.
References
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


